怎么理解本征无序态的蛋白质（Intrinsically disordered proteins）

见维基的解释：

An intrinsically disordered protein (IDP) is a protein that lacks a fixed or ordered three-dimensional structure.IDPs cover a spectrum of states from fully unstructured to partially structured and include random coils, (pre-)molten globules, and large multi-domain proteins connected by flexible linkers. They constitute one of the main types of protein (alongside globular, fibrous and membrane proteins).链接：https://en.wikipedia.org/wiki/Intrinsically_disordered_proteins

简单来说，就是一个蛋白质的三维结构呈现一个不固定的状态，如下图所示：

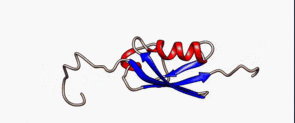
蛋白质的三维结构中间是固定的，C端和N端是游离状态的（不固定），此结构称为本征无序态的蛋白质。