偏差-方差均衡（Bias-Variance Tradeoff）

众所周知，对于线性回归，我们把目标方程式写成：。

（其中，f(x)是自变量x和因变量y之间的关系方程式，表示由噪音造成的误差项，这个误差是无法消除的）

对y的估计写成：。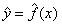

就是对自变量和因变量之间的关系进行的估计。一般来说，我们无从得之自变量和因变量之间的真实关系f(x)。假设为了模拟的缘故，我们设置了它们之间的关系（这样我们就知道了它们之间的真实关系），但即便如此，由于有这个irreducible error，我们还是无法得之真正的y是多少。当然，这并没有关系。因为我们想要知道的就是自变量和因变量之间的一般性关系，不需要把噪音计算进去。

通常我们使用一组训练数据让某个算法来进行学习，然后得到一个模型，这个模型能使损失函数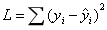最小。但是我们想要知道的是模型的泛化能力，也就是说我们需要模型在所有数据上都表现良好，而不仅仅是训练数据。假设我们知道所有的数据，然后把这些数据分成n组，我们把这n组数据在模型上进行测试，得到n个不同的损失函数。如果这些损失函数的平均值最小，也就是说真实数值和估计数值之间的差异平方的期望值最小，那就说明这个模型最理想。

此期望值的公式如下：

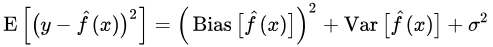
其中：

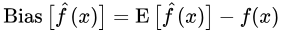
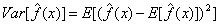
σ²是的方差

公式的推导过程如下（为简便起见，f(x)缩写成f，f(x)-hat缩写成f-hat）：

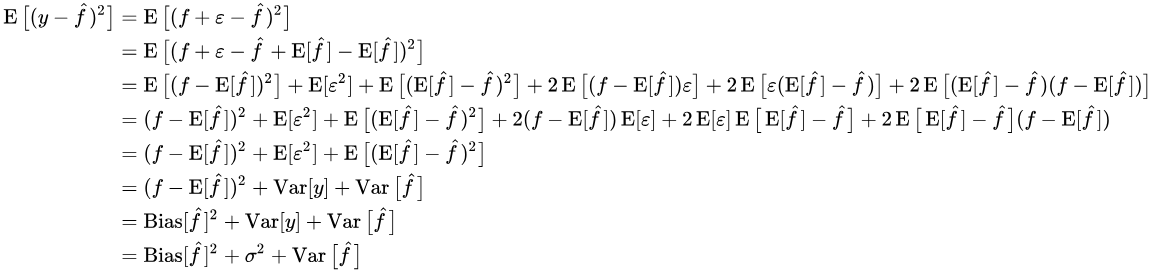
翻译成人话就是：

总泛化误差（Total Generalization Error） = 偏差（Bias） + 方差（Variance） + 无法消除的误差项（Irreducible Error）

我们要使总误差最小，就要想办法减少偏差和方差，因为最后一项是无法减少的。

现在让我们来看一下偏差和方差到底是什么。

偏差（bias）是指由于错误的假设导致的误差，比如说我们假设只有一个自变量能影响因变量，但其实有三个；又比如我们假设自变量和因变量之间是线性关系，但其实是非线性关系。其描述的是期望估计值和真实规律之间的差异。

方差（variance）是指通过n组训练数据学习拟合出来的结果之间的差异。其描述的是估计值和平均估计值之间差异平方的期望。

如果看了以上内容还是有点懵，那么看下面这张经典的图便可以理解：

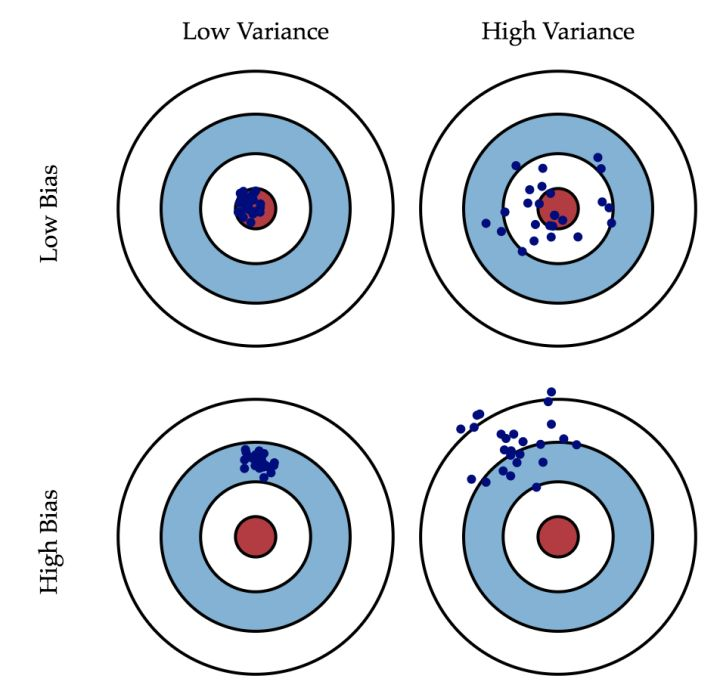
学习n次就相当于投靶n次。如果偏差小，同时方差又小，那就相当于每次都几乎正中靶心。这样的结果当然是最好的。如果偏差大，即使方差再小，那么投靶结果也还是离靶心有一段距离。反之，如果偏差小，但是方差很大，那么投靶结果将散布在靶心四周。

有人也许会说，只要偏差小，就算方差大一点也无所谓啊，只要把多次学习的结果平均一下，还是可以预测准确的；而如果偏差大的话，那就是连基本面都错了。但是这种认为减少偏差比减少方差更重要的想法是错误的，因为通常我们只有一组数据，而不是n组，我们的模型是依据我们已有的那组数据得出来的。因此，偏差和方差同样重要。

那么有没有可能让偏差小的同时又让方差小呢？这样我们不就能得到最好的结果了吗？但通过多次实验表明，事实不如人愿。

图1

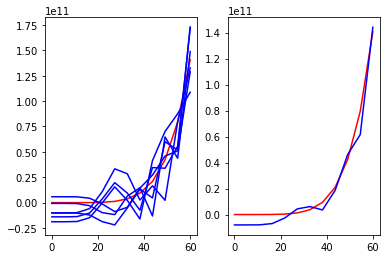
图2

红线是真实规律，左图蓝线是多次学习的结果，右图蓝线是平均结果。

图1是使用简单模型多次拟合的结果，可以看到其多次拟合的结果之间相差不大，但是平均结果和真实规律相差较大（也就是方差小，偏差大）；图2是使用较复杂的模型多次拟合的结果，可以看到其多次拟合的结果之间相差较大，但是平均结果和真实规律相差不大（也就是方差大，偏差小）。

总结来说就如下图所示，简单的模型偏差大，方差小；复杂的模型则相反，偏差小，方差大。随着模型越来越复杂，偏差逐渐减小，方差逐渐增大。我们发现无法在减少偏差的同时也减少方差。因此，我们需要找到一个折中的方案，即找到总误差最小的地方，这就叫做偏差-方差均衡（Bias-Variance Tradeoff）。

偏差-方差均衡这一概念贯穿整个机器学习，你随处都能见到它的身影。因此理解这一概念非常重要。

那么怎样才知道自己的模型是偏差大还是方差大呢？

高偏差：训练集误差大，验证集误差和训练集误差差不多大

高方差：训练集误差小，验证集误差非常大

又是如何解决高偏差或高方差问题呢？

高偏差问题：1，使用更复杂的模型

2，加入更多的特征

高方差问题：1，获取更多的数据

2，减少特征

3，正则化

以下是流程图：

偏差-方差的分解公式只在基于均方误差的回归问题上可以进行推导，但通过实验表明，偏差-方差均衡无论是对回归问题还是分类问题都是适用的。