Splay讲解
Splay讲解
Splay是平衡树的一种,是一种二叉搜索树,我们先讲解一下它的核心部分。
Splay的核心部分就是splay,可能有些人会说什么鬼?这样讲解是不是太不认真了?两个字回答:不是。第一个Splay是算法名称,而第二个splay是一个函数,如果说是一个函数,还不如说是两个函数,splay和rotate。下面开始讲解:
rotate
Splay最重要的部分就是两种基本旋转:zig,zag。本人在此理解的zig是左旋而zag是右旋。学过Treap的人可能会想到Treap的左右两旋,那两个旋转和这两个旋转是不一样的,Treap的旋转是讲自己的儿子旋上来,而Splay的旋转是将自己旋到父亲上去,两者的本质是不同的。
首先先讲解zag:我们要旋转的时候,一定会用到当前节点的父亲,所以我们需要存一个父亲数组,来记录当前节点的父亲是谁。当然我们还需要记录儿子是谁——左右两个儿子。现在就可以开始旋转了,如图(将B号节点旋到他的父亲A号节点的上方),是不是和treap的右旋十分相像?就是treap的右旋是在A号节点完成的,而zag是在B号节点完成的。
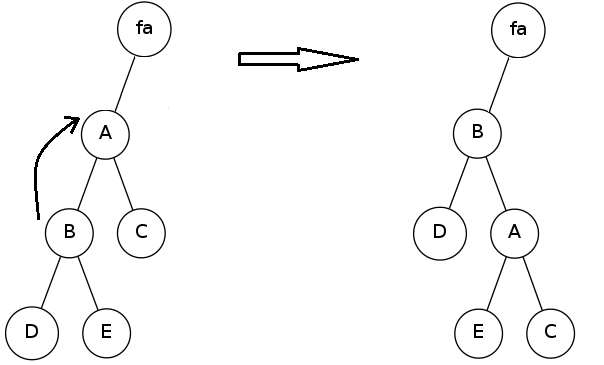
void zag(int p)
{
int tmp=fa[p],tmp2=fa[tmp];
lson[tmp]=rson[p],fa[rson[p]]=tmp;
rson[p]=tmp,fa[tmp]=p,fa[p]=tmp2;
if(lson[tmp2]==tmp) lson[tmp2]=p;
else rson[tmp2]=p;
update(tmp),update(p);
}
同理,zig就十分简单了,如图(将A号节点旋到他的父亲B号节点的上方)。
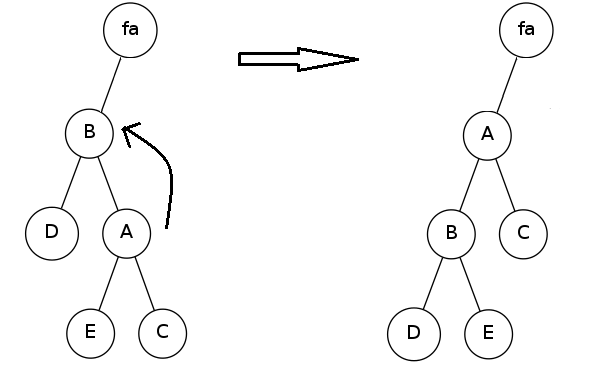
void zig(int p)
{
int tmp=fa[p],tmp2=fa[tmp];
rson[tmp]=lson[p],fa[lson[p]]=tmp;
lson[p]=tmp,fa[tmp]=p,fa[p]=tmp2;
if(lson[tmp2]==tmp) lson[tmp2]=p;
else rson[tmp2]=p;
update(tmp),update(p);
}
这就是zig和zag两种旋转,但我们大家仔细思考一下,这两个旋转的代码基本一致,是不是可以合成一个函数?答案是可以。我们开一个数组,为son[p][2],这个数组的含义就是p号节点的左右两个儿子,son[p][0]表示p号节点的左儿子,而son[p][1]表示p号节点的右儿子。这样我们进行旋转就十分方便了,我们进行一次check看我要左旋还是右旋就可以了,我们可以写一个chek函数返回值就是0和1,这样的话直接把返回值放在第二维就好了。
bool check(int p)
{
return p==son[fp][1];
}
void rotate(int p)
{
int tmp=fp;
int tmp2=ftp;
int tmp3;
check(p)?tmp3=1:tmp3=0;
fa[son[tmp][tmp3]=son[p][tmp3^1]]=tmp;
fa[p]=tmp2;
if(tmp2) son[tmp2][check(tmp)]=p;
fa[son[p][tmp3^1]=tmp]=p;
update(tmp),update(p);
}
旋转rotate讲解完毕,有问题可以发评论,我会解答。下面讲解splay,splay的功能就是将当前节点旋转到顶点,实际上就是一个循环。旋转一共有六种组合,下面我会逐个解释。
splay
第一种:当前节点直接就是根节点左儿子,直接zag就好啦。同理第二种:当前节点是根节点的右儿子,直接zig。
第三种(如左一图):我们需要先将当前节点的父亲旋转上去,再将自己旋转上去,就是先zag(父亲),再zag(自己)。同理第四种(如左二图):先zig(父亲),再zig(自己)。
第五种(入右二图):我们需要先将当前节点旋转上去,再讲他的父亲旋转上去,就是先zig(自己),再zag(父亲)。同理第六种(如右一图):先zag(自己),再zig(父亲)。
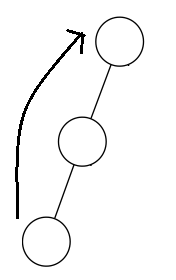
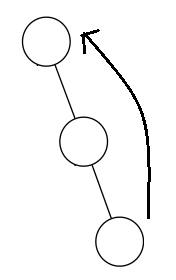
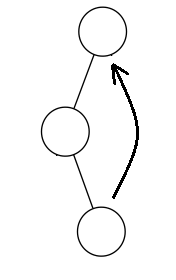
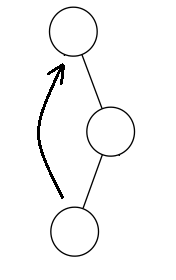
每次旋转的时候我们需要check一下具体实现比较简单。下面的代码是写的将当前节点旋转到指定的节点也就是所写(order),这样写的原因下面会说。
void splay(int p,int &order)
{
int tmp2=fa[order];
for(int tmp;(tmp=fp)!=tmp2;rotate(p))
if(ftp!=tmp2)
rotate(check(p)==check(tmp)?tmp:p);
order=p;
}
splay也讲解完毕,不会的也可以发评论问我。
区间操作
最后讲解一下splay比treap多出的操作,就是区间操作。这也就是为什么像上面那样书写代码,我们如果要对权值为[x,y]的这个区间进行操作,我们可以查找到x-1这个值的节点,将其旋转到root,再找到y+1这个值的节点,将其旋转到root的右儿子上。旋转之后,根据BST的性质,我们可以知道root的右儿子的左子树就是我们要的区间,直接进行操作就好啦,是不是很简单?
问题依旧可以发到评论之中。
Splay讲解的更多相关文章
- 【转】 史上最详尽的平衡树(splay)讲解与模板(非指针版spaly)
ORZ原创Clove学姐: 变量声明:f[i]表示i的父结点,ch[i][0]表示i的左儿子,ch[i][1]表示i的右儿子,key[i]表示i的关键字(即结点i代表的那个数字),cnt[i]表示i结 ...
- 平衡树之splay讲解
首先来说是splay是二叉搜索树,它可以说是线段树和SBT的综合,更可以解决一些二者解决不了的问题,splay几乎所有的操作都是由splay这一操作完成的,在介绍这一操作前我们先介绍几个概念和定义 二 ...
- [bzoj] 1588 营业额统计 || Splay板子题
原题 给出一个n个数的数列ai ,对于第i个元素ai定义\(fi=min(|ai-aj|) (1<=j<i)\),f1=a1,求\(/sumfi\) Splay板子题. Splay讲解:h ...
- 【模板】普通平衡树(权值splay)
安利splay讲解: [洛谷日报第62期]Splay简易教程 [模板]普通平衡树(luogu) Description 题目描述 您需要写一种数据结构(可参考题目标题),来维护一些数,其中需要提供以下 ...
- Splay代码简化版
皆さん.こんにちは.上一篇文章,我们讲了Splay如何实现.这一篇我们来让我们的伸展树短一点. 上一篇Splay讲解的链接:リンク. 首先还是变量的定义,在这里呢,我把一些小函数也用Define来实现 ...
- Algorithm lecture
当前标签: lecture 组合数求法讲解 BLADEVIL 2014-01-08 18:59 阅读:3 评论:0 mobius反演讲解 BLADEVIL 2014-01-08 18:13 ...
- 【专题】平衡树(Treap,fhq-treap)
[旋转] 平衡树中的旋转是指在不改变中序遍历的前提下改变树的形态的方式.(中序遍历=排名顺序) 右旋将当前点的左节点旋上来,左旋反之.(图侵删) void rturn(int &k){ int ...
- 平衡树及笛卡尔树讲解(旋转treap,非旋转treap,splay,替罪羊树及可持久化)
在刷了许多道平衡树的题之后,对平衡树有了较为深入的理解,在这里和大家分享一下,希望对大家学习平衡树能有帮助. 平衡树有好多种,比如treap,splay,红黑树,STL中的set.在这里只介绍几种常用 ...
- Play with Chain 【HDU - 3487】【Splay+TLE讲解】
题目链接 很好的一道题,用了三天多的时间,终于知道了我为什么T的原因,也知道了在Splay的同时该怎样子的节约时间,因为Splay本身就是大常数的O(N*logN),我们如果不在各种细节上节约时间,很 ...
随机推荐
- JAVA_SE基础——42.final修饰符
高手勿喷~ final关键字可用于修饰类.变量和方法,它有"这是无法改变的"或者"最终"的含义,因此被final修饰的类.变量和方法将具有以下特征: 1.fin ...
- LightningChart最新版 v.8.3 全新发布,新功能使用教程。
LightningChart最新版v.8.3全新发布,主要介绍以下五个新功能及使用教程. 1. 网格模型,三角鼠标追踪 Tracing MeshModels with mouse. Traced ...
- Python-面向对象(二)-Day7
1.字段 12.方法 43.属性 63.1.属性的基本使用 73.2.实例:对于主机列表 83.3.属性的两种定义方式 94.对于类的成员而言都有两种形式: 144.1.私有成员和公有成员的访问限制不 ...
- dubbo的InvocationChain
个人觉得dubbo比较好的设计是:一个是Cooma微容器设计.另一个就是InvocationChain了 Cooma微容器是自己实现了一套SPI,方便了用户做扩展: InvocationChain类似 ...
- JMM简介
JMM:Java Memory Model(Java内存模型),围绕着在并发过程中如何处理可见性.原子性.有序性这三个特性而建立的模型. 可见性:JMM提供了volatile变量定义.final.sy ...
- hive:数据库“行专列”操作---使用collect_set/collect_list/collect_all & row_number()over(partition by 分组字段 [order by 排序字段])
方案一:请参考<数据库“行专列”操作---使用row_number()over(partition by 分组字段 [order by 排序字段])>,该方案是sqlserver,orac ...
- css水平垂直居中的方法与 vertical-align 的用法
前言:这是笔者学习之后自己的理解与整理.如果有错误或者疑问的地方,请大家指正,我会持续更新! 1. 已知元素宽度 方法一:已知宽高,可以用position定位 + margin负值的方法 : 绝对定位 ...
- 微信小程序:wx.request之post请求后端无法获取数据的问题
前言:小程序的开发中总是踩到各种坑,看文档也不知所云: 例如当我们在写微信小程序接口时,method请求方式有POST和GET两种,为了数据安全,我们会偏向于使用POST请求方式访问服务器端: 问题: ...
- web攻击和防御措施
1.SQL注入:参照下面的链接 http://www.cnblogs.com/chenhaoyu/p/8758888.html 2.跨网站脚本攻击(Cross Site Scripting, XSS) ...
- Mybatis JPA 插件简介(v2.1.0)
相比之前的版本(v1.1.0),此版本(v2.1.0)做了较大的改动. 项目地址: github https://github.com/cnsvili/mybatis-jpa gitee https: ...
