qwe框架- CNN 实现

CNN实现

概述

我在qwe中有两种，第一种是按照Ng课程中的写法，多层循环嵌套得到每次的“小方格”，然后WX+b，这样的做法是最简单，直观。但是效率极其慢。基本跑个10张以内图片都会卡的要死。

第二种方法是使用img2col，将其转换为对应的矩阵，然后直接做一次矩阵乘法运算。

先看第一种

def forward(self, X):
        m, n_H_prev, n_W_prev, n_C_prev = X.shape
        (f, f, n_C_prev, n_C) = self.W.shape
        n_H = int((n_H_prev - f + 2 * self.pad) / self.stride) + 1
        n_W = int((n_W_prev - f + 2 * self.pad) / self.stride) + 1
        n_H, n_W, n_C = self.output_size

        Z = np.zeros((m, n_H, n_W, n_C))
        X_pad = zero_pad(X, self.pad)
        for i in range(m):
            for h in range(n_H):
                for w in range(n_W):
                    for c in range(n_C):
                        vert_start = h * self.stride
                        vert_end = vert_start + f
                        horiz_start = w * self.stride
                        horiz_end = horiz_start + f
                        A_slice_prev =X_pad[i,vert_start:vert_end, horiz_start:horiz_end, :]
                        Z[i,h,w,c] = conv_single_step(A_slice_prev, self.W[...,c], self.b[...,c])

def conv_single_step(X, W, b):
    # 对一个裁剪图像进行卷积
    # X.shape = f, f, prev_channel_size
    return np.sum(np.multiply(X, W) + b)

对于m,n_H,n_W,n_C循环就是取得裁剪小方块，可以看到这里的计算复杂度m * n_H * n_W * n_C * (f*f的矩阵计算)

第二种方法，先转换成大矩阵，再进行一次矩阵运算，相当于节省了多次小矩阵运算时间，这还是很可观的，能查个几十倍的速度。

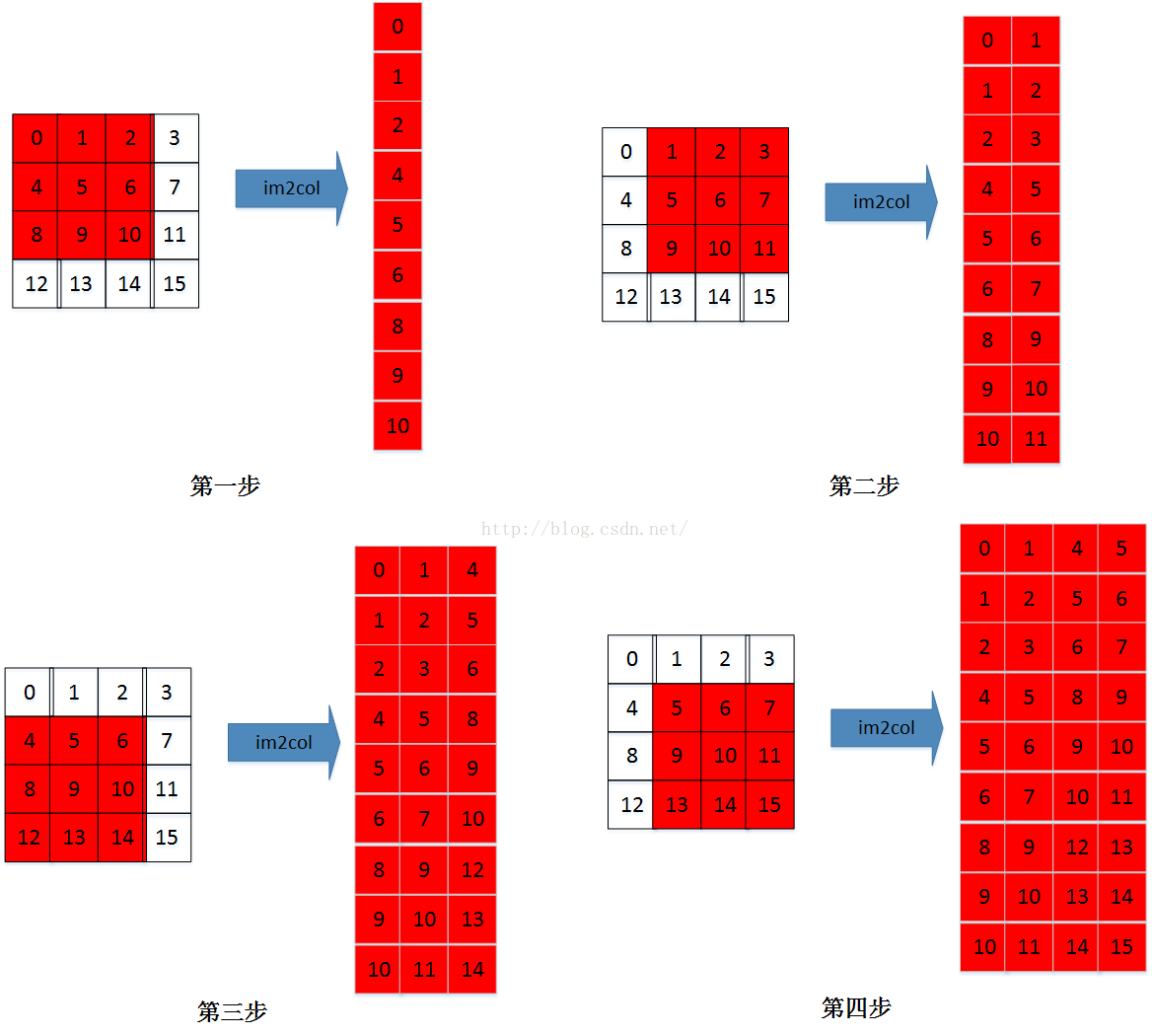
img2col原理很简单,详情可参考caffe im2col

就是循环将每一部分都拉长成一维矩阵拼凑起来。

对于CNN来说，H就是要计算方块的个数即m(样本数) n_H(最终生成图像行数)n_W(最终生成图像列数)，W就是f(核kernel长)f(核宽)*(输入样本通道输)

然后还要把参数矩阵W也拉成这个样子，H就是f(核长)f(核宽)(输入样本通道输)，W列数就是核数kernel_size

如下图

def img2col(X, pad, stride, f):
    pass
    ff = f * f
    m, n_H_prev, n_W_prev, n_C_prev= X.shape
    n_H = int((n_H_prev - f + 2 * pad) / stride) + 1
    n_W = int((n_W_prev - f + 2 * pad) / stride) + 1
    Z = np.zeros((m * n_H * n_W, f * f * n_C_prev))
    X_pad = np.pad(X, ((0, 0), (pad, pad), (pad, pad), (0, 0)), 'constant', constant_values=0)
    row = -1

    for i in range(m):
        for h in range(n_H):
            for w in range(n_W):
                row += 1
                vert_start = h * stride
                horiz_start = w * stride
                for col in range(f * f * n_C_prev):
                    t = col // n_C_prev
                    hh = t // f
                    ww = t % f
                    cc = col % n_C_prev
                    Z[row, col] = X_pad[i, vert_start + hh, horiz_start + ww, cc]

def speed_forward(model, X):
    W = model.W
    b = model.b
    stride = model.stride
    pad = model.pad
    (n_C_prev, f, f, n_C) = W.shape
    m, n_H_prev, n_W_prev, n_C_prev = X.shape

    n_H = int((n_H_prev - f + 2 * pad) / stride) + 1
    n_W = int((n_W_prev - f + 2 * pad) / stride) + 1

    # WW = W.swapaxes(2,1)
    # WW = WW.swapaxes(1,0)

    XX = img2col(X, pad, stride, f)
    # WW = WW.reshape(f*f*n_C_prev, n_C)
    WW = W.reshape(f*f*n_C_prev, n_C)
    model.XX = XX
    model.WW = WW

    Z = np.dot(XX, WW) + b
    return Z.reshape(m, n_H, n_W, n_C)

这种耗时操作，最好使用Cython扩展来写，不然速度还是不够理想。Cython扩展代码code

反向传播同理，具体代码参考

github