hdu1060 Leftmost Digit---求N的N次方的首位（对数）

题目链接：

http://acm.hdu.edu.cn/showproblem.php?pid=1060

题目描述：
求N的N次方的第一位。

思路：

第一次做这种类型的题目，学到了如何运用对数。

首先推导下述公式

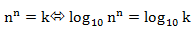
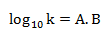
k的以10为底的对数值必定是A.B的形式，A为结果的整数部分，B为小数部分

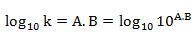
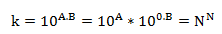
这里求nⁿ的首位只需要求出A.B = Nlog(N),然后取小数位即可，因为10^A并没有什么用，只要算出10^0.B

就算出了首位数字。这种方法可以用来求前i位。（i数值要小，因为运算精度有限）

 #include<iostream>
 #include<cstdio>
 #include<cmath>
 using namespace std;
 typedef long long ll;
 int T, n, m, cases;
 int main()
 {
     cin >> T;
     while(T--)
     {
         cin >> n;
         double s = 1.0 * n * log10(1.0 * n);
         s -= (ll)s;
         s = pow(, s);
         while(s < )s *= ;
         cout<<(int)(s)<<endl;
     }
     return ;
 }