「SDOI 2018」反回文串

题目大意：

　　求字符集大小为$k$长度为$n$的经循环移位后为回文串的数量。

题解：

　　这题是D1里最神的吧

　　考虑一个长度为$n$回文串，将其循环移位后所有的串都是满足要求的串。

　　但是显然这样计算会算重。考虑什么情况下会算重。

　　即当我们将这个回文串移位$x$后，发现这个新字符串为一个回文串时，必然接下来的移位都是重复的。

　　那么当$x$为多少时，新字符串为一个回文串？

　　我们稍加分析就会发现x一定和回文串的最小循环节$d$有关。

　　考虑最小循环节若为偶数时，当$x==d/2$时，则会变为一个新的回文串。

　　反之，$x==d$时，会出现一个新的回文串。

　　那么我们设$F(d)$表示长度为$n$，字符集为$k$，最小循环节为d的字符串的数量。

　　显然会有$\sum_{d|n}F(d)==k^{\lceil \frac{n}{2}\rceil}$。

　　设$G(n)=k^{\lceil \frac{n}{2}\rceil}$。

　　由莫比乌斯反演则有$F(d)=\sum_{n|d}\mu(\frac{n}{d})G(n)$。

　　那么考虑循环节$d$为偶数的串对答案贡献应该为$\frac{d}{2}*F(d)$这个我们在上面已经分析过了。

　　反之，则有其贡献为$d*F(d)$。

　　那么$Ans=\sum_{d|n}F(d)\frac{d}{1+[d为偶数]}$。

　　我们设$H(d)=\frac{d}{1+[d为偶数]}$。

　　　　

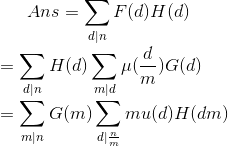
　　观察这个式子，发现直接求对于$1e18$的数据显然会T。考虑继续优化。

　　发现算法瓶颈在于$H(dm)$,思考$\sum_{d|x}\mu(d)*H(dm)$的性质。

　　由于$H(dm)$的值与奇偶性有关，那么我们分类讨论一下$m$和$\frac{n}{m}$之间奇偶性的关系。

　　考虑对于四种情况，我们（可以经过打表或者推导）会发现，当$m$为奇数且$\frac{n}{m}$为偶数时，$\sum_{d|\frac{n}{m}}\mu(d)H(dm)$为0,而另外三种情况都是$H(m)\sum_{d|\frac{n}{m}}\mu(d)H(d)$。

　　

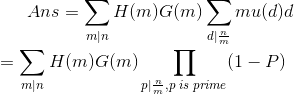
代码：

#include "bits/stdc++.h"

#define int long long

using namespace std;

inline int read () {
    int s=0,k=1;char ch=getchar();
    while (ch<'0'|ch>'9') ch=='-'?k=-1:0,ch=getchar();
    while (ch>47&ch<='9') s=s*10+(ch^48),ch=getchar();
    return s*k;
}

typedef long long ll;

inline ll R(ll x) {
    return 1ll*rand()*rand()%x;
}

inline ll Mult ( ll a,ll b ,ll mod) {
    return ( a*b - (ll)( (long double) a*b/mod )*mod + mod )% mod;
}

inline ll powmod(ll a,ll b,ll mod) {
    ll ret=1;
    while (b) {
        if (b&1) ret = Mult(ret,a,mod);
        b>>=1;a=Mult(a,a,mod);
    }
    return ret;
}

int prim[] = {2,3,5,7,11};

inline int Miller_Rabin(ll n) {
    if  (n==2) return true;
    int s=20,i,t=0;
    for (i=0;i<5;++i)
        if (n==prim[i]) return true;
        else if (n%prim[i]==0) return false;
    ll u=n-1,x[30];
    while (!(u&1))
        ++t,u>>=1;
   // printf("n=%lld u=%l\n",n);
    while (s--) {
        ll a=1ll*rand ()*rand()%(n-2)+2;
        x[0] = powmod (a,u,n);
        for (i=1;i<=t;++i) {
            x[i] = Mult(x[i-1],x[i-1],n);
            if (x[i]==1&&x[i-1]!=1&&x[i-1]!=n-1) return false;
        }
        if (x[t]!=1) return false ;
    }
    return true;
}

inline ll gcd (ll a,ll b) {
    return b?gcd(b,a%b):a;
}

inline ll Pollard_Rho(ll n,int c) {
    ll i=1,k=2,x=rand()%(n-1)+1,y=x;
  //  printf("n=%lld\n",n);
    while (1) {
        ++i ;
        x = (Mult(x,x,n) + c)%n;
        ll p = gcd (y-x+n,n);
        if (p!=1&&p!=n) return p;
        if (y==x) return n;
        if (i==k) {
            y=x;
            k<<=1;
        }
    }
} 

ll f[100],mod;
int cnt;

inline void find(ll n) {
    if (n==1) return ;
  //  printf("%lld\n",n);
    if (Miller_Rabin(n)) {
        f[++cnt]=n;
        return ;
    }
    //while (n==13);
    ll p=n;
    while (p==n) p = Pollard_Rho(n,R(n-1));
  //  printf("p=%lld\n",p);
    find(p);
    find(n/p);
}

ll n,k;

int m,num[100];
ll p[100][100];
ll ans;

inline void add (ll &x,ll y) {
    x+=y;
    //printf("x=%lld y=%lld mod=%lld\n",x,y,mod);
    if (x>=mod) x-=mod;
    if (x<0) x+=mod;
}

inline void dfs(int step,ll d,ll S) {
    if (step>m) {
        if ((d&1)==0&&(n/d&1)) return ;
        ll tmp=n/d;
        //printf("tmp=%lld d=%lld\n",tmp,d);
        //printf("k=%lld %lld %lld %lld\n",k,powmod(k,(tmp+1)/2,mod),((tmp&1)?tmp:tmp/2),S);
        add ( ans , Mult(Mult(powmod(k,(tmp+1)/2,mod),((tmp&1)?tmp:tmp/2),mod),S,mod));
        return ;
    }
    dfs (step+1,d,S);
    for (int i=1;i<=num[step];++i)
        dfs (step + 1, d*p[step][i],S*(1-p[step][1]));
    //printf("step=%d\n",step);
}

main ()
{
    //freopen("3.in","r",stdin);
    //freopen("3.out","w",stdout);
    int T=read();
    while (T--) {
        scanf("%lld%lld",&n,&k),mod=read();
        k%=mod;
        cnt=m=0;
        ans =0;
        find(n);
        sort(f+1,f+cnt+1);
        memset(p,0,sizeof p);
        for (int i=1,j=1;i<=cnt;i=j) {
            p[++m][0]=1;
            p[m][1]=f[i];
            num[m]=1;
           // printf("p=%lld\n",f[i]);
            for (j=i+1;j<=cnt;++j)
                if (f[j]!=f[j-1]) break;
                else p[m][j-i+1]=p[m][j-i]*f[j];
            num[m]=j-i;
          //  printf("num=%lld\n",num[m]);
        }
        dfs(1,1,1);
        printf("%lld\n",ans);
    }
    return 0;
}