LCA(最近公共祖先）之倍增算法

概述

对于有根树T的两个结点u、v，最近公共祖先LCA(T,u,v)表示一个结点x，满足x是u、v的祖先且x的深度尽可能大。

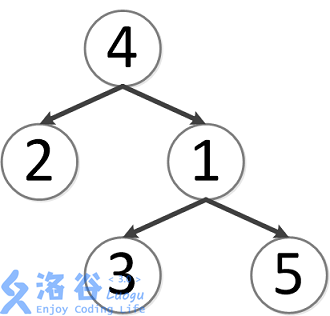
如图，3和5的最近公共祖先是1，5和2的最近公共祖先是4

在本篇中我们先介绍一下倍增算法

我们需要一个数组de[i]来表示每一个节点i的深度，用另一数组parent[i][j]来表示每一节点j向上走2的i次方是哪个节点

我们首先在初始化中算出每个点的深度和它的上一个点是什么（用parent[0][i]表示）

在此后我们进行倍增的处理：parent[1][j]=parent[0][parent[0][j]]......parent[i+1][j]=parent[i][parent[i][j]]

当然如果已经走到根节点了，就将其它的parent全设为0

然后我们就可以搞lca了：给你两个点想x，y，让y成为深的那个，如果x，y深度不等就让y倍增地往上跳。

当x，y深度相等时凡是它俩不相等就倍增地跳，最后它们中任意一个的父节点及他们的最近公共祖先

模板

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<cctype>
#include<cmath>
#include<cstdlib>
#include<queue>
#include<ctime>
#include<vector>
#include<set>
#include<map>
#include<stack>
using namespace std;
const int LOG=18;
vector<int>g[500010];
int de[500010];
int parent[LOG+3][500010];
void dfs(int now,int dep,int be)
{     parent[0][now]=be;
      de[now]=dep;
      for(int i=0;i<g[now].size();i++)
         if(g[now][i]!=be)
           dfs(g[now][i],dep+1,now);
}
int lca(int x,int y)
{     if(de[x]>de[y])swap(x,y);
         for(int i=LOG;i>=0;i--)
            if(de[parent[i][y]]>=de[x]&&parent[i][y]>0)
              y=parent[i][y];
      if(x==y)return x;
      for(int i=LOG;i>=0;i--)
         if(parent[i][x]!=parent[i][y])
           x=parent[i][x],y=parent[i][y];
      return parent[0][x];
}
int main()
{     int n,m,s,i,j,k,p,q;
      scanf("%d%d%d",&n,&m,&s);
      for(i=1;i<n;i++){
          int x,y;
          scanf("%d%d",&x,&y);
          g[x].push_back(y);
          g[y].push_back(x);
      }
      dfs(s,0,0);
      for(i=0;i<LOG;i++)
         for(j=1;j<=n;j++)
            if(parent[i][j]<=0)parent[i+1][j]=-1;
              else parent[i+1][j]=parent[i][parent[i][j]];
      for(i=1;i<=m;i++){
          int x,y;
          scanf("%d%d",&x,&y);
          printf("%d\n",lca(x,y));
      }
      return 0;
}