DLX算法一览
目录：
1 X思想的了解。
2. 链表的递归与回溯。
3. 具体操作。
4. 优化。
5. 一些应用与应用中的再次优化（例题）。
6. 练手题
X思想的了解。
首先了解DLX是什么？
DLX是一种多元未饱和型指令集结构，DLX 代表中级车、加长轴距版本、内饰改款、尊贵车豪华版车型。---百科百度
不不不，我不讲这些明明就是不懂
DLX是什么，一种解决精准覆盖问题的做法，一般不叫算法，下面讲。
模版题：
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
小Ho最近遇到一个难题，他需要破解一个棋局。
棋局分成了n行，m列，每行有若干个棋子。小Ho需要从中选择若干行使得每一列有且恰好只有一个棋子。
比如下面这样局面：
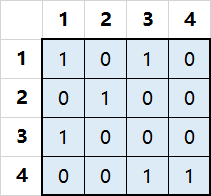
其中1表示放置有棋子的格子，0表示没有放置棋子。
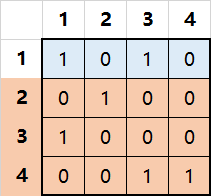
对于上面这个问题，小Ho经过多次尝试以后得到了解为选择2、3、4行就可以做到。
但是小Ho觉得自己的方法不是太好，于是他求助于小Hi。
小Hi：小Ho你是怎么做的呢？
小Ho：我想每一行都只有两种状态，选中和未被选中。那么我将选中视为1，未选中视为0。则每一种组合恰好对应了一个4位的01串，也就是一个4位的二进制数。
小Hi：恩，没错。
小Ho：然后我所做的就是去枚举每一个二进制数然后再来判定是否满足条件。
小Hi：小Ho你这个做法本身没什么问题，但是对于棋盘行数再多一点的情况就不行了。
小Ho：恩，我也这么觉得，那你有什么好方法么？
小Hi：我当然有了，你听我慢慢道来。
提示：跳舞链
输入
第1行：1个正整数t，表示数据组数，1≤t≤10。
接下来t组数据，每组的格式为：
第1行：2个正整数n,m，表示输入数据的行数和列数。2≤n,m≤100。
第2..n+1行：每行m个数，只会出现0或1。
输出
第1..t行：第i行表示第i组数据是否存在解，若存在输出"Yes"，否则输出"No"。
样例输入
2
4 4
1 1 0 1
0 1 1 0
1 0 0 0
0 1 0 1
4 4
1 0 1 0
0 1 0 0
1 0 0 0
0 0 1 1
样例输出
No
Yes
DL=Dancing Link跳舞链（双向十字链表），一种数据结构，用来优化X算法的，所以叫DLX，所以在严格意义上来讲，DLX就是一个优美的暴力可人家就是快，就是牛逼呀！
链表大家都知道，如果这都不知道，这篇文章你多半看不懂的！
双向十字链表是什么？
一个图祝大家秒记：
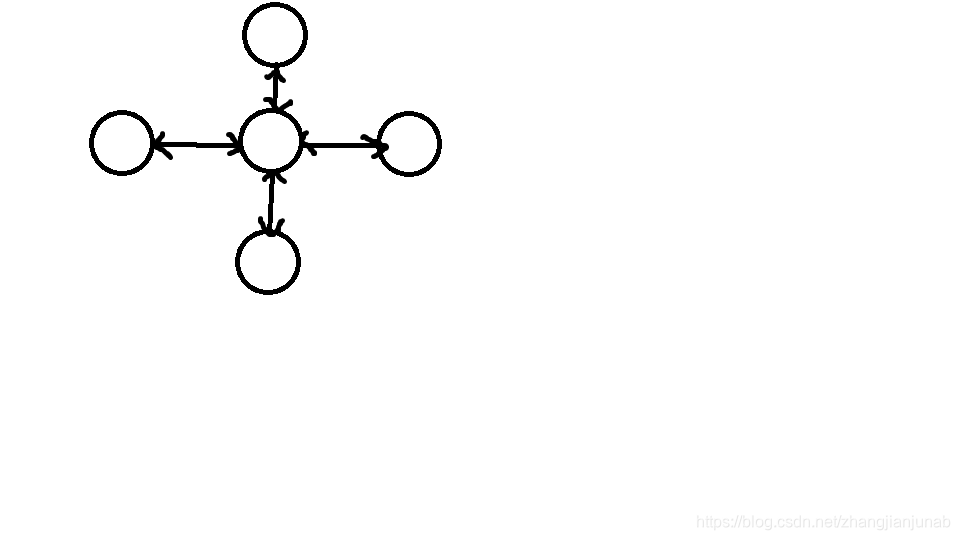
没错，双向十字链表有四个方向的链，而普通的双向链表只有两个方向的链。所以他更牛逼。
那么删除就更原来一样呀！
那么，X思想是什么。我是不是想Y了。。。
对于一个矩阵：
对于这种图，我们先找到第一个没有覆盖的列：
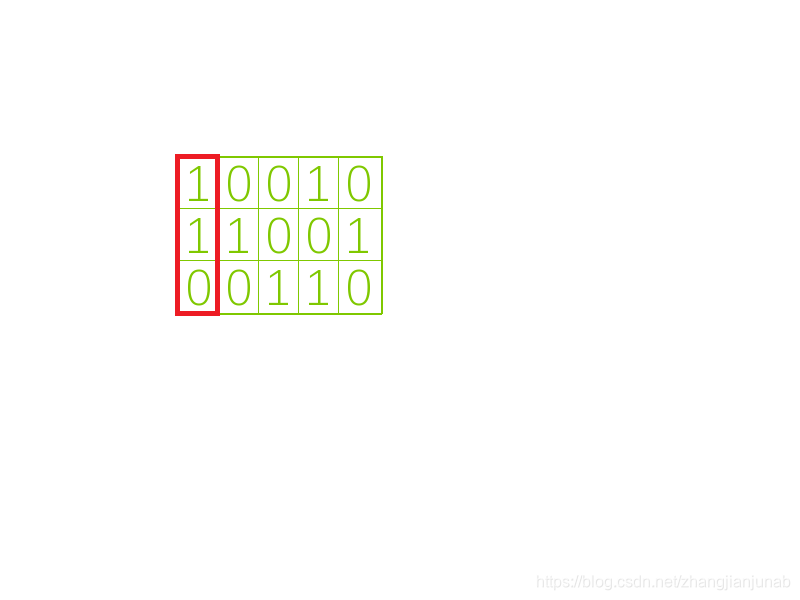
然后依次找一个这一列为1的行，然后将这一列与这一行标为紫色。
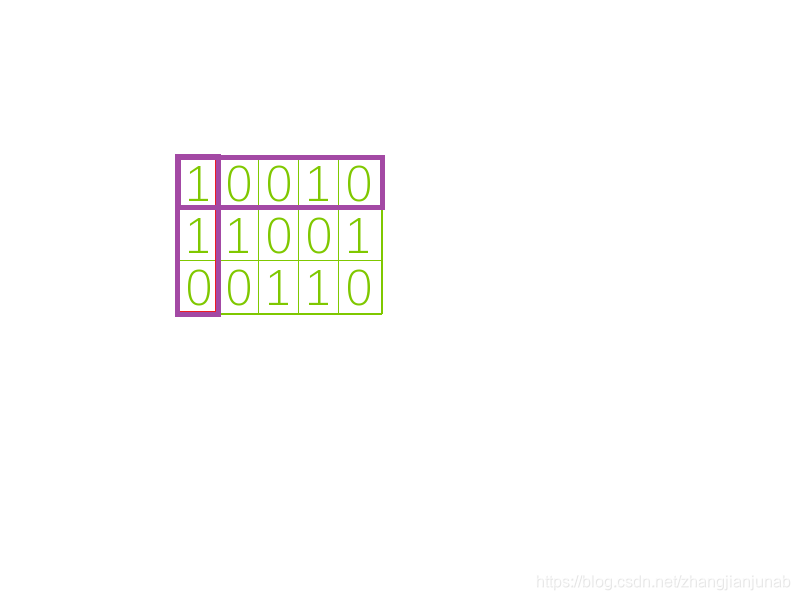
霸王硬上弓，删掉！
不对，删掉这一行还会有一行被覆盖。
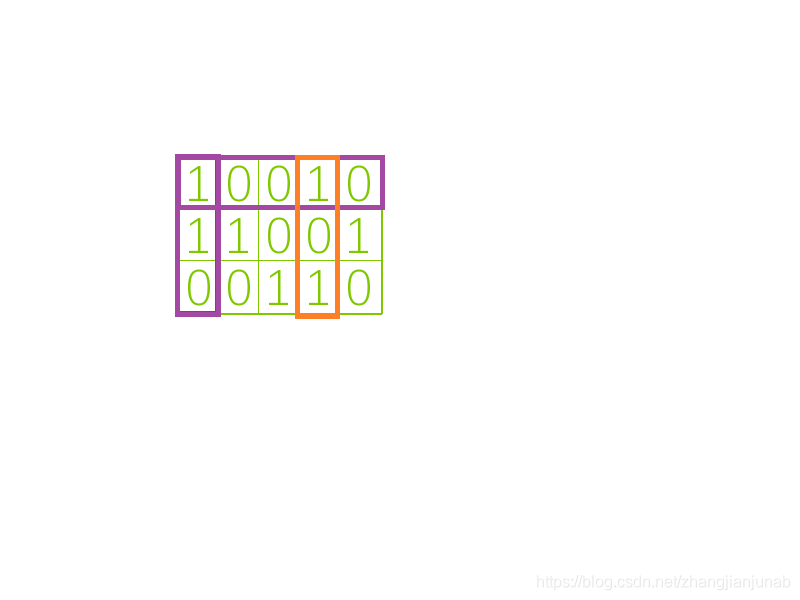
Look，这一行的橙色部分也被覆盖，因此橙色这一列也应该被删掉。
于是，我们应当把第三行删掉（蓝色部分）。
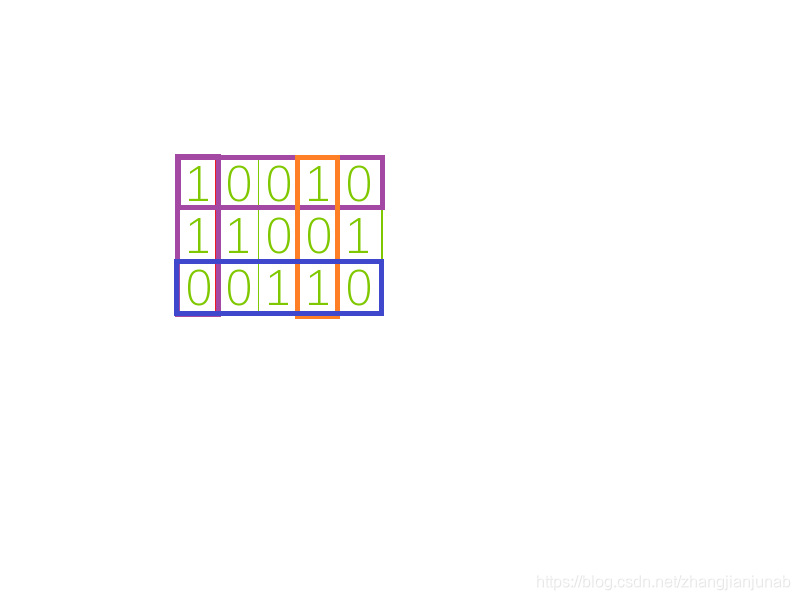
这样把所有被颜色圈住的格子删掉，同时将第一行丢入ans数组。
丑得一批。。。
那么，照旧，选择第一个没有被覆盖的列，第二列，同时我们选择第二行作为ans。
删除之后，我们继续找，发现第三列还没被覆盖，但是这一列没有一行有1了（完全连行都没有了。。。失败？）
不存在的，回溯大法好呀！
用填色的部分就是删除的部分（先将第一列删除，再将覆盖第一列的第一行与第二行删除，同时，我们选择了第二行，所以我们将第2、5行删除），同时我们将ans[1]=2。
这么一删，我们把第1、2、5列给删了，同时第1、2行也被删了，重复以下步骤，我们发现只要选择2、3行，就木有问题了。
但是，回溯过程代价打得一批这不是你画图丑得一批的理由！！！
链表的递归与回溯。
我们发现用链表不仅删除十分快，而且回溯也十分迅猛，在空间与时间上都十分优秀！
我们只需要用链表储存1的位置，同时，把每一列的编号也作为一个节点就可以了，然后用双向十字链表建个图，然后进行那些步骤（每次跳0号节点的右边，选列的话只需要跳选的节点的下面或上面，双向链表是循环的）。
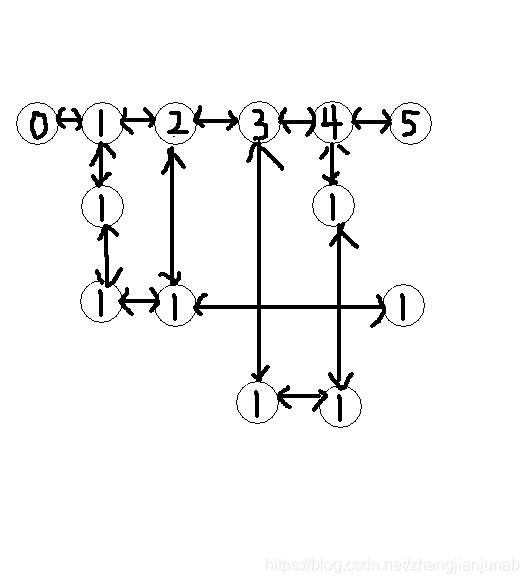
图中第一行中0、1、2、3、4、5代表列数，而下面的1代表这个节点的权值是1。
其实链表还有个重要的性质：
平常链表删除只是让左边的指向自己右边，同时右边又指向自己左边，但是自己的左边和右边还是指向他们的，如果要恢复的话，只需要让左边和右边的人再次指向自己就好了，真是方便。
不过双向十字链表要注意上下左右都要删除与他的联系。
所以为什么叫跳舞链，我怎么知道？
具体实现
定义代码：
#include<cstdio>
#include<cstring>
using namespace std;
int a[2100];//添加时记录第i个1所在的列数
struct node
{
int l,r,u,d,lie,hang;//l代表左,r代表右,u代表上，d代表下，lie代表lie标记，为优化做准备，而hang则是hang坐标，经常能有许多有用的信息。
};
struct DLX
{
node p[610000];int len;//p代表链表，len代表节点数
int size[2100],last[2100];//size代表第i列有多少节点，而last数组记录第i列的最后一个节点编号
inline void make(int l,int r,int u,int d,int lie,int hang){p[len].l=l;p[len].r=r;p[len].u=u;p[len].d=d;p[len].lie=lie;p[len].hang=hang;}//制造函数
inline void sxdel(int x){p[p[x].u].d=p[x].d;p[p[x].d].u=p[x].u;}//上下链表删除
inline void nsxdel(int x){p[p[x].u].d=p[p[x].d].u=x;}//上下链表还原
inline void zydel(int x){p[p[x].l].r=p[x].r;p[p[x].r].l=p[x].l;}//左右链表删除
inline void nzydel(int x){p[p[x].l].r=p[p[x].r].l=x;}//左右链表还原
}dlx;
初始化：
inline void clear(int x)//初始化x列
{
len=0;p[0].l=p[0].r=p[0].u=p[0].d=0;//将0号节点初始化
for(int i=1;i<=x;i++)//建x列
{
size[i]=0;last[i]=i;//重置size与last
len++;make(i-1,p[i-1].r,i,i,i,0);//make制造第i列节点
nzydel(i);//将左右的人指向自己
}
}
将第row行插入到链表里，插入的节点数为a[0]。
inline void add(int row)//添加第row行
{
if(a[0]==0)return ;//其实不加也可以，即使下面make了一个没用的节点，但是并不会访问到它
len++;make(len,len,last[a[1]],p[last[a[1]]].d,a[1],row);
nsxdel(len);size[a[1]]++;last[a[1]]=len;//制造本行第一个节点
for(int i=2;i<=a[0];i++)//遍历
{
len++;make(len-1,p[len-1].r,last[a[i]],p[last[a[i]]].d,a[i],row);//制造第i个节点
nsxdel(len);nzydel(len);size[a[i]]++;last[a[i]]=len;//让上下左右的节点指向自己。
}
}
删除（递归中的删除）：
//将第i列删除，同时将相关的行也彻底删除
inline void del(int x)//注意：x的行数为0
{
zydel(x);//先删掉第x列与其他列的练习
for(int i=p[x].u;i!=x;i=p[i].u)//找到这一列为1的行
{
for(int j=p[i].l;j!=i;j=p[j].l)sxdel(j),size[p[j].lie]--;//将这一行删掉。
}
}
回溯：
//这就不多讲了，不过就反过来罢了
inline void back(int x)//x的行数为0
{
nzydel(x);
for(int i=p[x].u;i!=x;i=p[i].u)
{
for(int j=p[i].l;j!=i;j=p[j].l)nsxdel(j),size[p[j].lie]++;
}
}
优化
还没讲重点吧！
我们发现，输出答案的话，与一开始选择的列数并没有多大关系（原本是直接选择p[0].r），所以我们可以选择列数中节点最少的作为对象，减少递归次数！
//递归过程
int dance(int x)
{
if(!p[0].r)return x;//结束，返回
int first,mi=999999999;
for(int i=p[0].r;i;i=p[i].r)//找最少列
{
if(size[p[i].lie]<mi)mi=size[p[i].lie],first=i;
}
if(mi==0)return 0;//有一列没有办法覆盖？返回0
del(first);//先删除
for(int i=p[first].u;i!=first;i=p[i].u)
{
for(int j=p[i].l;j!=i;j=p[j].l)del(p[j].lie);//将这一行能覆盖的区域删除
int tt=dance(x+1);//递归
if(tt)return tt;
for(int j=p[i].l;j!=i;j=p[j].l)back(p[j].lie);//回溯
}
back(first);
return 0;
}
这样就完了？
其实这样还很慢！
注意这里：
for(int j=p[i].l;j!=i;j=p[j].l)del(p[j].lie);//将这一行能覆盖的区域删除
int tt=dance(x+1);//递归
if(tt)return tt;
for(int j=p[i].l;j!=i;j=p[j].l)back(p[j].lie);//回溯
我们发现：
原本在删除的时候，第一个列与第二个列中相交的行数在第一次删除就没了，但是在回溯的时候，第一个列与第二个列中相交的行数在第一次回溯又回来了，而第二列中又多遍历了一遍，后面也是如此！
但是，这么打就没问题了：
for(int j=p[i].l;j!=i;j=p[j].l)del(p[j].lie);//将这一行能覆盖的区域删除
int tt=dance(x+1);//递归
if(tt)return tt;
for(int j=p[i].r;j!=i;j=p[j].r)back(p[j].lie);//回溯
完整代码：
#include<cstdio>
#include<cstring>
using namespace std;
int a[2100];//添加时记录第i个1所在的列数
struct node
{
int l,r,u,d,lie,hang;//l代表左,r代表右,u代表上，d代表下，lie代表lie标记，为优化做准备，而hang则是hang坐标，经常能有许多有用的信息。
};
struct DLX
{
node p[610000];int len;//p代表链表，len代表节点数
int size[2100],last[2100];//size代表第i列有多少节点，而last数组记录第i列的最后一个节点编号
inline void make(int l,int r,int u,int d,int lie,int hang){p[len].l=l;p[len].r=r;p[len].u=u;p[len].d=d;p[len].lie=lie;p[len].hang=hang;}//制造函数
inline void sxdel(int x){p[p[x].u].d=p[x].d;p[p[x].d].u=p[x].u;}//上下链表删除
inline void nsxdel(int x){p[p[x].u].d=p[p[x].d].u=x;}//上下链表还原
inline void zydel(int x){p[p[x].l].r=p[x].r;p[p[x].r].l=p[x].l;}//左右链表删除
inline void nzydel(int x){p[p[x].l].r=p[p[x].r].l=x;}//左右链表还原
inline void clear(int x)//初始化x列
{
len=0;p[0].l=p[0].r=p[0].u=p[0].d=0;//将0号节点初始化
for(int i=1;i<=x;i++)//建x列
{
size[i]=0;last[i]=i;//重置size与last
len++;make(i-1,p[i-1].r,i,i,i,0);//make制造第i列节点
nzydel(i);//将左右的人指向自己
}
}
inline void add(int row)//添加第row行
{
if(a[0]==0)return ;//其实不加也可以，即使下面make了一个没用的节点，但是并不会访问到它
len++;make(len,len,last[a[1]],p[last[a[1]]].d,a[1],row);
nsxdel(len);size[a[1]]++;last[a[1]]=len;//制造本行第一个节点
for(int i=2;i<=a[0];i++)//遍历
{
len++;make(len-1,p[len-1].r,last[a[i]],p[last[a[i]]].d,a[i],row);//制造第i个节点
nsxdel(len);nzydel(len);size[a[i]]++;last[a[i]]=len;//让上下左右的节点指向自己。
}
}
//将第i列删除，同时将相关的行也彻底删除
inline void del(int x)//注意：x的行数为0
{
zydel(x);//先删掉第x列与其他列的练习
for(int i=p[x].u;i!=x;i=p[i].u)//找到这一列为1的行
{
for(int j=p[i].l;j!=i;j=p[j].l)sxdel(j),size[p[j].lie]--;//将这一行删掉。
}
}
//这就不多讲了，不过就反过来罢了
inline void back(int x)//x的行数为0
{
nzydel(x);
for(int i=p[x].u;i!=x;i=p[i].u)
{
for(int j=p[i].l;j!=i;j=p[j].l)nsxdel(j),size[p[j].lie]++;
}
}
//递归过程
int dance(int x)
{
if(!p[0].r)return x;//结束，返回
int first,mi=999999999;
for(int i=p[0].r;i;i=p[i].r)//找最少列
{
if(size[p[i].lie]<mi)mi=size[p[i].lie],first=i;
}
if(mi==0)return 0;//有一列没有办法覆盖？返回0
del(first);//先删除
for(int i=p[first].u;i!=first;i=p[i].u)
{
for(int j=p[i].l;j!=i;j=p[j].l)del(p[j].lie);//将这一行能覆盖的区域删除
int tt=dance(x+1);//递归
if(tt)return tt;
for(int j=p[i].r;j!=i;j=p[j].r)back(p[j].lie);//回溯
}
back(first);
return 0;
}
}dlx;
int main()
{
int T;scanf("%d",&T);//多组数据
while(T--)
{
int n,m;scanf("%d%d",&n,&m);//输入
dlx.clear(m);//初始化
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
int x;scanf("%d",&x);
if(x)a[++a[0]]=j;
}
dlx.add(i);
a[0]=0;//找到1的数量
}
if(dlx.dance(0))printf("Yes\n");//输出
else printf("No\n");
}
return 0;
}
至此，普通DLX讲完了。
一些应用与应用中的再次优化（例题）。
啊哈，DLX只能解决精准覆盖问题？这么鸡肋？
不存在的！
其实，他还可以装逼、成为神犇通过转换模型等一系列方法做出一些要不断优化暴力才可以做出来的毒瘤题！
先介绍第一种应用：
重复覆盖问题
如题目所讲，在精准覆盖问题中，每一列只能被一个1覆盖，在这里可以被多个1覆盖，但是仍然要求每一列都要被覆盖，求最少用几行可以达到要求。
至于例题，上网搜神龙的问题，我上不去，所以。。。
但是，有一个更不错的例题哪里更不错了。。。
Radar
传送门！
T组数据
有N个城市，M个雷达，每次最多用K个雷达。
给你他们的坐标，判断雷达半径最少为多少才可以覆盖所有的城市。
- 1 ≤ T ≤ 20
- 1 ≤ N, M ≤ 50
- 1 ≤ K ≤ M
- 0 ≤ X, Y ≤ 1000
先输入N、M、K
然后给你N个城市的坐标与M个雷达的坐标（整数）
输出最小半径（保留6位小数）
1
3 3 2
3 4
3 1
5 4
1 1
2 2
3 3
2.236068
嗯，一道不错的二分DLX练手题
首先，二分+重复覆盖问题
删除选择的这一行与这一列
删除与回溯：
inline void del(int x)//删除第x列，x的行数不为0
{
for(int i=p[x].u;i!=x;i=p[i].u)zydel(i);
}
inline void back(int x)//回溯，x的行数不为0
{
for(int i=p[x].u;i!=x;i=p[i].u)nzydel(i);
}
嗯，然后我们就A了
真香。。。。
这就AC了？那么刀片店就要倒闭了。。。
因为del函数的变动，整个矩阵密度下降特别慢，结果导致悲剧的发生。
这个时候，我们就要用类似A中的期望函数了！（为什么不是IDA？没有迭代加深）。
期望函数就是：如果将能够覆盖当前列的所有行全部选中，去掉这些行能够覆盖到的列，将这个操作作为一步操作。重复此操作直到所有列都被覆盖时用了多少步，加上现在的步数，如果大于当前最小函数，就return ;
这样的话，我们的重复覆盖问题也可以快得猛如虎了！
至于做法，二分半径，然后把城市当成列，然后雷达当成行，将雷达能覆盖的城市设为1，然后DLX，判断最小选的行数如果小于等于K，就合法。
上代码！
#include<cstdio>
#include<cstring>
#include<cmath>
#pragma GCC optimize(2)//不，你没有看到这句话
using namespace std;
typedef long long ll;
const ll inf=1e8;
int a[100],ans=0;
struct node
{
int l,r,u,d,lie,hang;
};//双向十字链表
struct DLX
{
//大多函数以前打过注释，就不打了
node p[210000];int len;
int size[100],last[100];
inline void make(int l,int r,int u,int d,int lie,int hang){p[len].l=l;p[len].r=r;p[len].u=u;p[len].d=d;p[len].lie=lie;p[len].hang=hang;}
inline void sxdel(int x){p[p[x].u].d=p[x].d;p[p[x].d].u=p[x].u;}
inline void nsxdel(int x){p[p[x].u].d=p[p[x].d].u=x;}
inline void zydel(int x){p[p[x].l].r=p[x].r;p[p[x].r].l=p[x].l;}
inline void nzydel(int x){p[p[x].l].r=p[p[x].r].l=x;}
inline void clear(int x)
{
p[0].l=p[0].r=p[0].u=p[0].d=0;len=0;
for(int i=1;i<=x;i++)
{
size[i]=0;last[i]=i;
len++;make(i-1,p[i-1].r,i,i,i,0);
nzydel(len);
}
}
inline void add(int row)
{
if(!a[0])return ;
len++;make(len,len,last[a[1]],p[last[a[1]]].d,a[1],row);
nsxdel(len);size[a[1]]++;last[a[1]]=len;
for(int i=2;i<=a[0];i++)
{
len++;make(len-1,p[len-1].r,last[a[i]],p[last[a[i]]].d,a[i],row);
nsxdel(len);nzydel(len);size[a[i]]++;last[a[i]]=len;
}
}
inline void del(int x)//删除第x列，x的行数不为0
{
for(int i=p[x].u;i!=x;i=p[i].u)zydel(i);
}
inline void back(int x)//回溯，x的行数不为0
{
for(int i=p[x].u;i!=x;i=p[i].u)nzydel(i);
}
bool vis[100];
inline int ex()//A*期望函数
{
int ret=0;
for(int i=p[0].r;i;i=p[i].r)vis[i]=true;//初始化
for(int i=p[0].r;i;i=p[i].r)
{
if(vis[i])
{
ret++;
vis[i]=false;
for(int j=p[i].u;j!=i;j=p[j].u)
{
for(int kk=p[j].l;kk!=j;kk=p[kk].l)vis[p[kk].lie]=false;
}
}
}
return ret;
}
void dance(int x)
{
if(x+ex()>=ans)return ;//A*优化
if(p[0].r==0)//得出答案
{
ans=x;
return ;
}
int first=0,mi=999999999;
for(int i=p[0].r;i;i=p[i].r)
{
if(size[p[i].lie]<mi)mi=size[p[i].lie],first=i;
}
if(mi==0)return ;
for(int i=p[first].u;i!=first;i=p[i].u)
{
del(i);//注意，不是del(first);
for(int j=p[i].l;j!=i;j=p[j].l)del(j);//不是p[j].lie
dance(x+1);
for(int j=p[i].r;j!=i;j=p[j].r)back(j);//回溯
back(i);//回溯
}
}
}dlx;
struct pointss
{
double x,y;
}lei[100],city[100];
inline double dis(pointss x,pointss y){return sqrt((x.x-y.x)*(x.x-y.x)+(x.y-y.y)*(x.y-y.y));}//计算距离
int main()
{
int T;scanf("%d",&T);
while(T--)
{
int n,m,k;scanf("%d%d%d",&n,&m,&k);
for(int i=1;i<=n;i++)scanf("%lf%lf",&city[i].x,&city[i].y);
for(int i=1;i<=m;i++)scanf("%lf%lf",&lei[i].x,&lei[i].y);//把他当成小数，方便以后计算dis
ll l=0,r=1e11,mid,anss;//将double转成long long
while(l<=r)
{
mid=(l+r)/2;
double WXP=mid/100000000.0;//计算出半径
dlx.clear(n);
for(int i=1;i<=m;i++)
{
a[0]=0;
for(int j=1;j<=n;j++)
{
if(dis(city[j],lei[i])<=WXP)a[++a[0]]=j;//建图。
}
dlx.add(i);
}
ans=999999999;dlx.dance(0);
if(ans<=k)anss=mid,r=mid-1;
else l=mid+1;
}
printf("%.6lf\n",anss/100000000.0);//输出
}
return 0;
}
数独才讲到
题目：
9*9数独
约束条件：
- 一个格子填一个数字。
- 一行每个数字填一个。
- 一列每个数字填一个。
- 一宫每个数字填一个。
把约束条件变成列：
先把第一个约束条件写出来，用81列来代表，在i行j列填代表覆盖\((i-1)*9+j\)列
第二个约束条件，也用81列来代表，在第i行填k代表覆盖\(81+(i-1)*9+k\)列
第三个约束条件，也用81列来代表，在第j列填k代表覆盖\(162+(j-1)*9+k\)列
第四个约束条件，我们用一个公式计算出每个数字在第几宫：\(((i-1)/3)*3+(j-1)/3+1\)，而在第\(((i-1)/3)*3+(j-1)/3+1\)宫填k代表覆盖\(243+(((i-1)/3)*3+(j-1)/3)*9+k\)列。
然后把第i行第j列填k代表行，处理出他能覆盖那些列，建图，然后跑一遍，OK
但是我们还可以优化，由于数独中某些格子被填过，所以我们可以把这些格子所覆盖的区域先删掉，就可以达到优化时间的效果！
顺便提一下，这里面的行就可以起到带有附加权值的效果。
至于代码。。。丑
#include<cstdio>
#include<cstring>
#include<cstdlib>
using namespace std;
int a[1000];
struct point
{
int x,y,c;
inline void zh(int tt){x=(tt-1)/81+1;y=((tt-1)%81)/9+1;c=((tt-1)%9)+1;}//将tt值转回来
}ans[1000];
struct node
{
int l,r,u,d,lie,hang;
};
node p[210000];int len;
int size[1000],last[1000],map[11][11];
bool bol[1000];
inline void make(int l,int r,int u,int d,int lie,int hang){p[len].l=l;p[len].r=r;p[len].u=u;p[len].d=d;p[len].lie=lie;p[len].hang=hang;}
inline void sxdel(int x){p[p[x].u].d=p[x].d;p[p[x].d].u=p[x].u;}
inline void nsxdel(int x){p[p[x].u].d=p[p[x].d].u=x;}
inline void zydel(int x){p[p[x].l].r=p[x].r;p[p[x].r].l=p[x].l;}
inline void nzydel(int x){p[p[x].l].r=p[p[x].r].l=x;}
inline void clear(int x)
{
len=0;p[0].l=p[0].r=p[0].u=p[0].d=0;
for(int i=1;i<=x;i++)
{
len++;make(i-1,p[i-1].r,i,i,i,0);
nzydel(i);size[i]=0;last[i]=i;
}
}
inline void add(int row)
{
if(!a[0])return ;
len++;make(len,len,last[a[1]],p[last[a[1]]].d,a[1],row);
nsxdel(len);size[a[1]]++;last[a[1]]=len;
for(int i=2;i<=a[0];i++)
{
len++;make(len-1,p[len-1].r,last[a[i]],p[last[a[i]]].d,a[i],row);
nsxdel(len);nzydel(len);size[a[i]]++;last[a[i]]=len;
}
}
inline void del(int x)
{
zydel(x);
for(int i=p[x].u;i!=x;i=p[i].u)
{
for(int j=p[i].r;j!=i;j=p[j].r)
{
sxdel(j),size[p[j].lie]--;
}
}
}
inline void back(int x)
{
nzydel(x);
for(int i=p[x].d;i!=x;i=p[i].d)
{
for(int j=p[i].l;j!=i;j=p[j].l)nsxdel(j),size[p[j].lie]++;
}
}
inline bool dance(int x)
{
//打了无数遍的代码
if(!p[0].r)
{
for(int i=1;i<=x;i++)
{
map[ans[i].x][ans[i].y]=ans[i].c;
}
for(int i=1;i<=9;i++)
{
for(int j=1;j<=8;j++)printf("%d ",map[i][j]);
printf("%d\n",map[i][9]);
}
return true;
}
int first=0,mi=999999999;
for(int i=p[0].r;i;i=p[i].r)
{
if(size[p[i].lie]<mi)mi=size[p[i].lie],first=p[i].lie;
}
if(mi==0)return false;
del(first);
for(int i=p[first].u;i!=first;i=p[i].u)
{
for(int j=p[i].l;j!=i;j=p[j].l)del(p[j].lie);
ans[x+1].zh(p[i].hang);
if(dance(x+1))return true;
for(int j=p[i].r;j!=i;j=p[j].r)back(p[j].lie);
}
back(first);
return false;
}
int main()
{
memset(bol,false,sizeof(bol));//清0
clear(4*9*9);
for(int i=1;i<=9;i++)
{
for(int j=1;j<=9;j++)
{
scanf("%d",&map[i][j]);
if(map[i][j])
{
bol[(i-1)*9+j]=true;
// dlx.del((i-1)*9+j);
bol[81+(i-1)*9+map[i][j]]=true;
// dlx.del(81+(i-1)*9+dlx.map[i][j]);
bol[162+(j-1)*9+map[i][j]]=true;
// dlx.del(162+(j-1)*9+dlx.map[i][j]);
bol[243+(((i-1)/3)*3+(j-1)/3)*9+map[i][j]]=true;
// dlx.del(243+(((i-1)/3)*3+(j-1)/3)*9+dlx.map[i][j]);
}
else
{
for(int k=1;k<=9;k++)//枚举k
{
if(!bol[81+(i-1)*9+k] && !bol[162+(j-1)*9+k] && !bol[243+(((i-1)/3)*3+(j-1)/3)*9+k])
{
a[0]=0;
a[++a[0]]=(i-1)*9+j;
a[++a[0]]=81+(i-1)*9+k;
a[++a[0]]=162+(j-1)*9+k;
a[++a[0]]=243+(((i-1)/3)*3+(j-1)/3)*9+k;
add((i-1)*81+(j-1)*9+k);
}
}
}
}
}
for(int i=1;i<=324;i++)//这个要打在外面，因为如果在for循环里面删除的话，会因为last并没有更新而导致在add里面把删除的节点重新还原
{
if(bol[i])del(i);
}
dance(0);
return 0;
}
浪费了我大好青春
练手题
八皇后：
传送门
提示：通过想约束条件，构建矩阵，不过要想清楚，斜线的情况
不懂看代码：
//与数独不同的地方标出来了
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
using namespace std;
int a[1000],jie,anslen,now[50],n;
struct jians
{
int a[20];
}anss[100000];
inline bool cmp(jians x,jians y)
{
for(int i=1;i<=n;i++)
{
if(x.a[i]!=y.a[i])return x.a[i]<y.a[i];
}
return true;
}
struct node
{
int l,r,u,d,lie,hang;
};
struct DLX
{
node p[1000];int len;
int size[1000],last[1000];
inline void make(int l,int r,int u,int d,int lie,int hang){p[len].l=l;p[len].r=r;p[len].u=u;p[len].d=d;p[len].lie=lie;p[len].hang=hang;}
inline void sxdel(int x){p[p[x].u].d=p[x].d;p[p[x].d].u=p[x].u;}
inline void nsxdel(int x){p[p[x].u].d=p[p[x].d].u=x;}
inline void zydel(int x){p[p[x].l].r=p[x].r;p[p[x].r].l=p[x].l;}
inline void nzydel(int x){p[p[x].l].r=p[p[x].r].l=x;}
inline void clear(int x)
{
len=0;p[0].l=p[0].r=p[0].u=p[0].r=0;size[0]=999999999;
for(int i=1;i<=x;i++)
{
len++;make(i-1,p[i-1].r,i,i,i,0);
nzydel(len);size[i]=0;last[i]=i;
}
}
inline void add(int row)
{
if(!a[0])return ;
len++;make(len,len,last[a[1]],p[last[a[1]]].d,a[1],row);
nsxdel(len);size[a[1]]++;last[a[1]]=len;
for(int i=2;i<=a[0];i++)
{
len++;make(len-1,p[len-1].r,last[a[i]],p[last[a[i]]].d,a[i],row);
nsxdel(len);nzydel(len);size[a[i]]++;last[a[i]]=len;
}
}
inline void del(int x)
{
zydel(x);
for(int i=p[x].u;i!=x;i=p[i].u)
{
for(int j=p[i].l;j!=i;j=p[j].l)sxdel(j),size[p[j].lie]--;
}
}
inline void back(int x)
{
nzydel(x);
for(int i=p[x].u;i!=x;i=p[i].u)
{
for(int j=p[i].l;j!=i;j=p[j].l)nsxdel(j),size[p[j].lie]++;
}
}
inline void dance(int x)
{
if(p[0].r>jie || !p[0].r)//这里不一样
{
anslen++;
for(int i=1;i<=n;i++)anss[anslen].a[i]=now[i];
return ;//记录答案
}
int mi=0;
for(int i=p[0].r;i<=jie;i=p[i].r)//稍稍有不同
{
if(size[p[i].lie]<size[p[mi].lie])mi=i;
}
del(mi);
for(int i=p[mi].u;i!=mi;i=p[i].u)
{
for(int j=p[i].l;j!=i;j=p[j].l)del(p[j].lie);
now[(p[i].hang-1)/n+1]=(p[i].hang-1)%n+1 ;
dance(x+1);
for(int j=p[i].r;j!=i;j=p[j].r)back(p[j].lie);
}
back(mi);
}
}dlx;
inline int mymin(int x,int y){return x<y?x:y;}
int main()
{
scanf("%d",&n);
dlx.clear(6*n-2);jie=2*n;//由于斜线有2n-1个，所以只需满足横线与竖线的要求
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
a[0]=0;
a[++a[0]]=i;
a[++a[0]]=n+j;
a[++a[0]]=(2*n+(j-i)+n);
a[++a[0]]=(4*n-1+(i+j)-1);
dlx.add((i-1)*n+j);//建图不同
}
}
dlx.dance(0);
sort(anss+1,anss+anslen+1,cmp);//排序
int edd=mymin(3,anslen);
for(int i=1;i<=edd;i++)
{
for(int j=1;j<n;j++)printf("%d ",anss[i].a[j]);
printf("%d\n",anss[i].a[n]);
}
printf("%d\n",anslen);
return 0;
}
//右斜：j-i+n
//左斜：i+j-1
靶型数独：
传送门
DLX轻松AC：
#include<cstdio>
#include<cstring>
using namespace std;
int a[1000],ans=-1,now;
int p[11][11]=
{
{0,0,0,0,0,0,0,0,0,0,0},
{0,6,6,6,6,6,6,6,6,6,0},
{0,6,7,7,7,7,7,7,7,6,0},
{0,6,7,8,8,8,8,8,7,6,0},
{0,6,7,8,9,9,9,8,7,6,0},
{0,6,7,8,9,10,9,8,7,6,0},
{0,6,7,8,9,9,9,8,7,6,0},
{0,6,7,8,8,8,8,8,7,6,0},
{0,6,7,7,7,7,7,7,7,6,0},
{0,6,6,6,6,6,6,6,6,6,0}
};
struct node
{
int l,r,u,d,lie,hang,c;
};
struct DLX
{
node p[210000];int len;
int size[1000],last[1000];
bool bol[1000];
void make(int l,int r,int u,int d,int lie,int hang,int c){p[len].l=l;p[len].r=r;p[len].u=u;p[len].d=d;p[len].lie=lie;p[len].hang=hang;p[len].c=c;}
void sxdel(int x){p[p[x].u].d=p[x].d;p[p[x].d].u=p[x].u;}
void nsxdel(int x){p[p[x].u].d=p[p[x].d].u=x;}
void zydel(int x){p[p[x].l].r=p[x].r;p[p[x].r].l=p[x].l;}
void nzydel(int x){p[p[x].r].l=p[p[x].l].r=x;}
void clear(int x)
{
len=0;p[0].l=p[0].r=p[0].u=p[0].d=0;size[0]=999999999;
for(int i=1;i<=x;i++)
{
len++;make(i-1,p[i-1].r,i,i,i,0,0);
nzydel(len);size[i]=0;last[i]=i;
}
}
void add(int row,int dis)
{
if(!a[0])return ;
len++;make(len,len,last[a[1]],p[last[a[1]]].d,a[1],row,dis);
nsxdel(len);size[a[1]]++;last[a[1]]=len;
for(int i=2;i<=a[0];i++)
{
len++;make(len-1,p[len-1].r,last[a[i]],p[last[a[i]]].d,a[i],row,dis);
nsxdel(len);nzydel(len);size[a[i]]++;last[a[i]]=len;
}
}
void del(int x)
{
zydel(x);
for(int i=p[x].u;i!=x;i=p[i].u)
{
for(int j=p[i].l;j!=i;j=p[j].l)sxdel(j),size[p[j].lie]--;
}
}
void back(int x)
{
nzydel(x);
for(int i=p[x].u;i!=x;i=p[i].u)
{
for(int j=p[i].l;j!=i;j=p[j].l)nsxdel(j),size[p[j].lie]++;
}
}
int ex(int x){return 4050-x;}//A*剪枝，大概就是说假设每个格子的分数都是10，总分数是多少
void dance(int x)
{
if(now+ex(now)<=ans)return ;//A*
if(!p[0].r)
{
if(now>ans)ans=now;//记录答案
return ;
}
int mi=0;
for(int i=p[0].l;i;i=p[i].l)
{
if(size[p[i].lie]<size[p[mi].lie])mi=i;
}
if(!size[p[mi].lie])return ;
del(mi);
for(int i=p[mi].u;i!=mi;i=p[i].u)
{
for(int j=p[i].l;j!=i;j=p[j].l)del(p[j].lie);
now+=p[i].c;
dance(x+1);
now-=p[i].c;
for(int j=p[i].r;j!=i;j=p[j].r)back(p[j].lie);
}
back(mi);
}
}dlx;
int main()
{
memset(dlx.bol,false,sizeof(dlx.bol));
dlx.clear(324);
for(int i=1;i<=9;i++)
{
for(int j=1;j<=9;j++)
{
int x;scanf("%d",&x);
if(x!=0)
{
dlx.bol[(i-1)*9+j]=true;
dlx.bol[81+(i-1)*9+x]=true;
dlx.bol[162+(j-1)*9+x]=true;
dlx.bol[243+(((i-1)/3)*3+(j-1)/3)*9+x]=true;
now+=x*p[i][j];
}
else
{
for(int k=9;k>=1;k--)
{
if(!dlx.bol[81+(i-1)*9+k] && !dlx.bol[162+(j-1)*9+k] && !dlx.bol[243+(((i-1)/3)*3+(j-1)/3)*9+k])
{
a[0]=0;
a[++a[0]]=(i-1)*9+j;
a[++a[0]]=81+(i-1)*9+k;
a[++a[0]]=162+(j-1)*9+k;
a[++a[0]]=243+(((i-1)/3)*3+(j-1)/3)*9+k;
dlx.add((i-1)*81+(j-1)*9+k,k*p[i][j]);//建图
}
}
}
}
}
for(int i=1;i<=324;i++)//数独的剪枝
{
if(dlx.bol[i])dlx.del(i);
}
dlx.dance(0);
printf("%d\n",ans);
return 0;
}
完结撒花
DLX算法一览的更多相关文章
- 关于用舞蹈链DLX算法求解数独的解析
欢迎访问——该文出处-博客园-zhouzhendong 去博客园看该文章--传送门 描述 在做DLX算法题中,经常会做到数独类型的题目,那么,如何求解数独类型的题目?其实,学了数独的构建方法,那么DL ...
- 搜索：DLX算法
精确覆盖问题:在一个0-1矩阵中,选定部分行,使得每一列都有且只有一个1.求解一种选法 舞蹈链(Dance Link),也就是一个循环十字链表,可以快速的删掉和恢复某行某列 结合了舞蹈链的搜索就称作D ...
- 【DLX算法】hdu3498 whosyourdaddy
题意:给你一个01矩阵,让你选择尽可能少的行数,使得这些行的并集能够覆盖到所有列. DLX算法求解重复覆盖问题模板,使用估价函数进行剪枝. #include<cstdio> #includ ...
- 【DLX算法】poj2676 Sudoku
DLX算法求解精确覆盖问题模板.赛场上可以参见白书. #include<cstdio> #include<cstring> #include<vector> usi ...
- 精确覆盖DLX算法模板另一种写法
代码 struct DLX { int n,id; int L[maxn],R[maxn],U[maxn],D[maxn]; ]; int H[ms]; ) //传列长 { n=nn; ;i<= ...
- 精确覆盖DLX算法模板
代码 struct DLX { int n,id; int L[maxn],R[maxn],U[maxn],D[maxn]; ]; ) //传列长 { n=nn; ;i<=n;i++) U[i] ...
- <转>机器学习系列(9)_机器学习算法一览（附Python和R代码）
转自http://blog.csdn.net/han_xiaoyang/article/details/51191386 – 谷歌的无人车和机器人得到了很多关注,但我们真正的未来却在于能够使电脑变得更 ...
- React Diff算法一览
前言 diff算法一直是React系统最核心的部分,并且由于演化自传统diff,使得比较方式从O(n^3)降级到O(n),然后又改成了链表方式,可谓是变化万千. 传统Diff算法 传统diff算法需要 ...
- 简单面试前算法一览java
1.排序 冒泡,快速排序 2.查找 二分查找 3.链表 翻转链表 合并链表 是否有环 b. 快慢指针 public class QuickSort { public static void qui ...
随机推荐
- check_mk的性能案例
http://wiki.lustre.org/Check_MK/Graphite/Graphios_Setup_Guide Dell PowerEdge R515 2x 8-Core AMD Opte ...
- SQL Server ->> Transparent Data Encryption(透明化数据加密)
Comming later... 参考文献: Transparent Data Encryption (TDE)
- SpringMvc-helloword
说明:在此只说明helloword的简单实现,通过helloword例子先了解springMvc是这样工作的,然后在一步步的研究原理 配置web.xml 1.配置servlet servlet-cla ...
- Third week-homework(员工管理系统)
需求: 可以查询员工所有信息 可以修改员工信息 可以增加新员工 code: import sys,json # yuangong = { # "1": ["faker&q ...
- 7 - py面向对象一条龙服务
Python从设计之初就已经是一门面向对象的语言,在python里所有东西皆是对象. 下面通过一个实例来说明什么是面向对象. 引子 你是一家公司的员工,公司现在要开发一款“人狗战争”的游戏,人狗战争肯 ...
- spring-4.3.16+xfire-spring-1.2.6版本升级
最近爆了个spring的漏洞,然后公司整体要求升级spring到最新版本,然后搞四了一大批猿人. spring-4.*的最新版本是4.3.16(稳定版) xfire-spring-1.2.6(最新版- ...
- bzoj3820 虫逢
Description 小强和阿米巴是好朋友. 阿米巴告诉小强,变形虫(又叫阿米巴虫)和绝大多数生物一样,也是有 DNA 的.并且,变形虫可以通过分裂的方式进行无性繁殖. 我们把一个变形虫的基因组抽象 ...
- SPOJ MUSKET - Musketeers
黑书P117页. 要是不看解析,确实不要算和定义状态. 把环看成链,是指把这个1234512345,写两边,然后怎么表示一个人是否胜利了呢?其实就是其他人全部死光(好像等于没说): 考虑最后一次杀人, ...
- 【[Violet]樱花】
就是化柿子 我们求 \[\frac{1}{x}+\frac{1}{y}=\frac{1}{n!}\] 的正整数解的个数 喜闻乐见的化柿子了 \[\frac{x+y}{xy}=\frac{1}{n!}\ ...
- [APIO/CTSC 2007]数据备份
嘟嘟嘟 这竟然是一道贪心题,然而我在不看题解之前一直以为是dp. 首先最优的配对一定是相邻两个建筑物配对,所以我们求出差分数组,就变成了在n - 1个数中选出不相邻的k个数,使这k个数的和最小. 贪心 ...