Manacher算法——最长回文子串

一、相关介绍

最长回文子串

• s="abcd", 最长回文长度为 1，即a或b或c或d
• s="ababa", 最长回文长度为 5，即ababa
• s="abccb", 最长回文长度为 4，即bccb
• 问题：现给你一个非常长的字符串，请求出其最长回文子串

解决方法

传统解决问题的思路是遍历每一个字符，以该字符为中点向两边查找。其时间复杂度为 O(n²)，很不高效。

1975年，一个叫Manacher的人发明了一个算法，Manacher 算法（中文名：马拉车算法），该算法可以把时间复杂度提升到 O(n)。

下面来看看马拉车算法是如何工作的。

二、Manacher算法

【算法流程】

由于回文分为偶回文（比如 bccb）和奇回文（比如 bcacb），而在处理奇偶问题上会比较繁琐，所以这里我们使用一个技巧，具体做法是，在字符串首尾，及字符间各插入一个字符（前提这个字符未出现在串里）。

举个例子：s="abbahopxpo"，转换为s_new="$#a#b#b#a#h#o#p#x#p#o#"（这里的字符 $ 只是为了防止越界，下面代码会有说明），如此，s 里起初有一个偶回文abba和一个奇回文opxpo，被转换为#a#b#b#a#和#o#p#x#p#o#，长度都转换成了奇数。

定义一个辅助数组int p[]，其中p[i]表示以 i 为中心的最长回文的半径，例如：

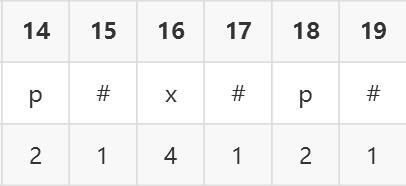
可以看出，p[i] - 1正好是原字符串中最长回文串的长度。

接下来的重点就是求解 p 数组，如下图：

设置两个变量，mx 和 id 。mx 代表以 id 为中心的最长回文的右边界，也就是mx = id + p[id]。

假设我们现在求p[i]，也就是以 i 为中心的最长回文半径，如果i < mx，如上图，那么：

if (i < mx)
    p[i] = min(p[2 * id - i], mx - i);

2 * id - i为 i 关于 id 的对称点，即上图的 j 点，而p[j]表示以 j 为中心的最长回文半径，因此我们可以利用p[j]来加快查找。

【加深理解】

根据回文的性质，p[i]的值基于以下三种情况得出：

（1）j 的回文串有一部分在 id 的之外，如下图：

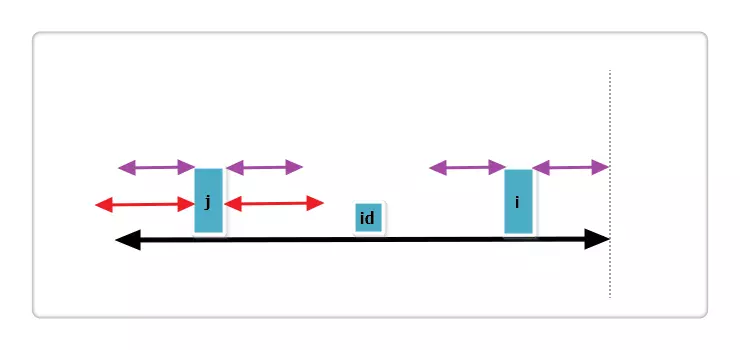
上图中，黑线为 id 的回文，i 与 j 关于 id 对称，红线为 j 的回文。那么根据代码此时p[i] = mx - i，即紫线。那么p[i]还可以更大么？答案是不可能！见下图：

假设右侧新增的紫色部分是p[i]可以增加的部分，那么根据回文的性质，a 等于 d ，也就是说 id 的回文不仅仅是黑线，而是黑线 + 两条紫线，矛盾，所以假设不成立，故p[i] = mx - i，不可以再增加一分。

（2）j 回文串全部在 id 的内部，如下图：

根据代码，此时p[i] = p[j]，那么p[i]还可以更大么？答案亦是不可能！见下图：

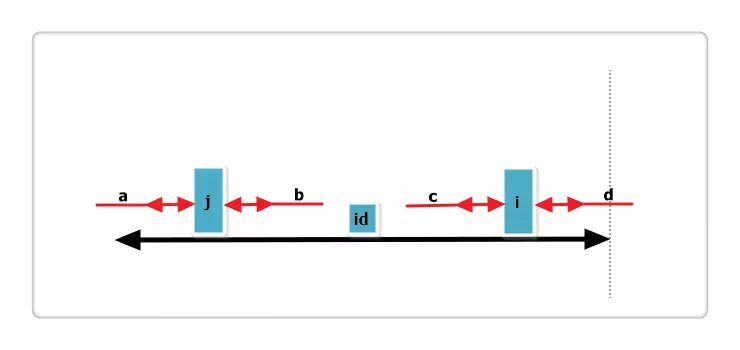
假设右侧新增的红色部分是p[i]可以增加的部分，那么根据回文的性质，a 等于 b ，也就是说 j 的回文应该再加上 a 和 b ，矛盾，所以假设不成立，故p[i] = p[j]，也不可以再增加一分。

（3）j 回文串左端正好与 id 的回文串左端重合，见下图：

根据代码，此时p[i] = p[j]或p[i] = mx - i，并且p[i]还可以继续增加，所以需要

while (s_new[i - p[i]] == s_new[i + p[i]])
    p[i]++;

根据（1）（2）（3），很容易推出 Manacher 算法的最坏情况，即为字符串内全是相同字符的时候。在这里我们重点研究Manacher()中的 for 语句，推算发现 for 语句内平均访问每个字符 5 次，即时间复杂度为：T_worst(n)=O(n)。

同理，我们也很容易知道最佳情况下的时间复杂度，即字符串内字符各不相同的时候。推算得平均访问每个字符 4 次，即时间复杂度为：T_best(n)=O(n)。

综上，Manacher 算法的时间复杂度为 O(n)。

三、代码实现

#include<iostream>
#include<string.h>
#include<algorithm>
using namespace std;

char s[1000];
char s_new[2000];
int p[2000];

int Init()
{
    int len = strlen(s);
    s_new[0] = '$';
    s_new[1] = '#';
    int j = 2;

    for (int i = 0; i < len; i++)
    {
        s_new[j++] = s[i];
        s_new[j++] = '#';
    }

    s_new[j] = '\0';  //别忘了哦

    return j;  //返回s_new的长度
}

int Manacher()
{
    int len = Init();  //取得新字符串长度并完成向s_new的转换
    int max_len = -1;  //最长回文长度

    int id;
    int mx = 0;

    for (int i = 1; i < len; i++)
    {
        if (i < mx)
            p[i] = min(p[2 * id - i], mx - i);  //需搞清楚上面那张图含义, mx和2*id-i的含义
        else
            p[i] = 1;

        while (s_new[i - p[i]] == s_new[i + p[i]])  //不需边界判断，因为左有'$',右有'\0'
            p[i]++;

        //我们每走一步i，都要和mx比较，我们希望mx尽可能的远，这样才能更有机会执行if (i < mx)这句代码，从而提高效率
        if (mx < i + p[i])
        {
            id = i;
            mx = i + p[i];
        }

        max_len = max(max_len, p[i] - 1);
    }

    return max_len;
}

int main()
{

    while (printf("请输入字符串：\n"))
    {
        scanf("%s", s);
        printf("最长回文长度为 %d\n\n", Manacher());
    }

    return 0;
}