POJ 2161 Chandelier（动态规划）

Description

Lamps-O-Matic company assembles very large chandeliers. A chandelier consists of multiple levels. On the first level crystal pendants are attached to the rings. Assembled rings and new pendants are attached to the rings of the next level, and so on. At the end there is a single large ring -- the complete chandelier with multiple smaller rings and pendants hanging from it.  A special-purpose robot assembles chandeliers. It has a supply of crystal pendants and empty rings, and a stack to store elements of a chandelier during assembly. Initially the stack is empty. Robot executes a list of commands to assemble a chandelier. 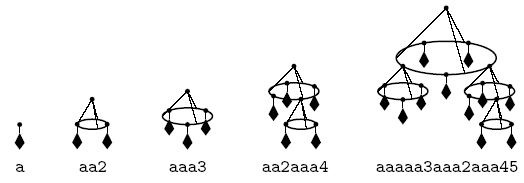On command "a" robot takes a new crystal pendant and places it on the top of the stack. On command "1" to "9" robot takes the corresponding number of items from the top of the stack and consecutively attaches them to the new ring. The newly assembled ring is then placed on the top of the stack. At the end of the program there is a single item on the stack -- the complete chandelier.  Unfortunately, for some programs it turns out that the stack during their execution needs to store too many items at some moments. Your task is to optimize the given program, so that the overall design of the respective chandelier remains the same, but the maximal number of items on the stack during the execution is minimal. A pendant or any complex multi-level assembled ring count as a single item of the stack.  The design of a chandelier is considered to be the same if each ring contains the same items in the same order. Since rings are circular it does not matter what item is on the top of the stack when the robot receives a command to assemble a new ring, but the relative order of the items on the stack is important. For example, if the robot receives command "4" when items < i1, i2, i3, i4 > are on the top of the stack in this order (i1 being the topmost), then the same ring is also assembled if these items are arranged on the stack in the following ways: < i2, i3, i4, i1 >, or < i3, i4, i1, i2 >, or < i4, i1, i2, i3 >.

Input

The input contains a single line with a valid program for the robot. The program consists of at most 10 000 characters.

Output

On the first line of the output file write the minimal required stack capacity (number of items it can hold) to assemble the chandelier. On the second line write some program for the assembly robot that uses stack of this capacity and results in the same chandelier.

题目大意：太难说了不写了。

思路： 大概就是递推处理对每个数字组合起来所需要的最小栈吧……思路挺难搞的我已经不会描述了……

---

转http://hi.baidu.com/billdu/item/50dd9fb49364269619469705

方法就是每到一个数字命令，就枚举前面的元素怎样排列。由于保证了元素数目不多于9，所以圆排列只用枚举9个，时间上绰绰有余。

枚举一个情况下的计算是重点。设定任意一个元素【操作时要占用的最大堆栈数】为m，比如说，组装这个元素以前栈中有5个元素，中间的某一步栈中有12个元素，并且自始至终没超过12个，那么该元素的的M = 7。单个元素的M为1。（这很容易理解……）

然后设某数字指令要拼装的的元素集合为A，元素的安装位置设为p的话（头一个元素是第0个，之后是第1个，依此类推），在这种枚举的情况下目标元素的m = max{ p(E) + m(E), E∈A }，因为对于每一个元素，在这之前已经安装了p(E)个元素，安装本元素需要再开m(E)的空间。枚举所有情况，找出最小的目标m记录下来，直到最后最终的元素的m值就是所要用的栈。

输出方案很简单，只需要递归输出，注意顺序既可。

---

 #include <cstdio>
 #include <iostream>
 #include <cstring>
 #include <algorithm>
 #include <cctype>
 using namespace std;

 const int MAXN = ;

 char s[MAXN];
 int src[MAXN], n;

 void init() {
     int i;
     for(i = ; s[i]; ++i)
         src[i] = isdigit(s[i]) * (s[i] - '');
     n = i;
 }

 int best[MAXN];
 int ans[MAXN][];
 int pos[];
 int stk[MAXN], top;

 void next(int *arr, int n) {
     for(int i = ; i < n; ++i)
         if(++arr[i] >= n) arr[i] = ;
 }

 void solve(int n) {
     if(src[n] == ) {
         best[n] = ;
         stk[top++] = n;
         return ;
     }
     int &len = src[n];
     for(int i = ; i < len; ++i) pos[i] = i;
     for(int i = ; i < len; ++i) {
         int tmp = len;
         for(int j = ; j < len; ++j)
             tmp = max(tmp, j + best[stk[top - len + pos[j]]]);
         if(best[n] ==  || tmp < best[n]) {
             best[n] = tmp;
             for(int j = ; j < len; ++j) ans[n][j] = stk[top - len + pos[j]];
         }
         next(pos, len);
     }
     top -= len;
     stk[top++] = n;
 }

 void dfs(int n) {
     for(int i = ; i < src[n]; ++i)
         if(src[ans[n][i]]) dfs(ans[n][i]);
         else putchar('a');
     printf("%d", src[n]);
 }

 int main() {
     scanf("%s", s);
     init();
     for(int i = ; i < n; ++i) solve(i);
     printf("%d\n", best[n - ]);
     dfs(n - );
     puts("");
 }