CF1137F Matches Are Not a Child's Play（树链剖分）

题面

我们定义一棵树的删除序列为：每一次将树中编号最小的叶子删掉，将该节点编号加入到当前序列的最末端，最后只剩下一个节点时将该节点的编号加入到结尾。

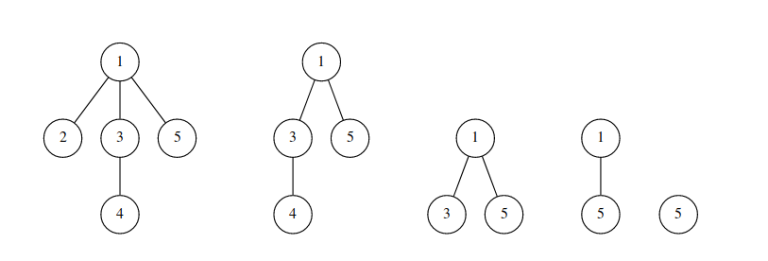
例如对于上图中的树，它的删除序列为：2 4 3 1 5

现在给出一棵\(n\)个节点的树，有\(m\)次操作：

\(up\) \(v\)：将\(v\)号节点的编号变为当前所有节点编号的\(\max + 1\)

\(when\) \(v\)：查询\(v\)在当前树的删除序列中是第几号元素

\(compare\) \(u\) \(v\)：查询\(u\)和\(v\)在当前树的删除序列中谁更靠前

题解

放火烧山，牢底坐穿

首先我们考虑一下，设当前树上优先度最高的点为\(u\)，此时一个\(up\)操作，使得\(v\)成为了优先度最高的点，那么这棵树烧起来的时候会发生什么事

首先\(uv\)之间这条路肯定会最后才烧着，而且是从\(u\)烧到\(v\)，而其它所有节点烧的相对顺序都是不变的

那么可以理解为，我们定义一个时间戳\(tim\)，每次\(up\)操作的时候\(++tim\)，并记录一下这个时间戳路径的起点\(u\)，然后把\(uv\)路径上全都覆盖上这个时间戳。那么，一个节点第几个被烧呢？显然就是所有时间戳小于它的点的点数，再加上它到自己时间戳的起点\(u\)的距离

每一次都是区间覆盖，有没有让你想到什么呢？

对，这很像珂朵莉树。我们可以先树剖，对于每一条重链，维护一个\(set\)，\(set\)里维护这条重链上的颜色区间。那么一次区间覆盖只要把旧的区间删去，并加入新的区间就行了。不过因为要维护每种颜色的点的个数，所以我们可能还需要用一个树状数组，再删除和插入区间的时候维护一下点的个数

还有个问题是我们需要算出一开始的答案，直接把每个点暴力\(up\)就行了

虽然说着像珂朵莉树不过这里的复杂度应该是严格的。每一次路径修改会被拆成\(O(\log n)\)个区间，每个被拆出来的区间最多插入一次删除一次。以及我们中间有可能需要把一个区间拆成两半，一次是询问的时候要把一个点拆出来看看它的时间戳是啥，那么这一部分拆出的区间总数是\(O(n)\)的。还有就是我们插入区间的时候有可能会拆掉区间，不过这种情况下拆出的区间最多一个，所以一次路径覆盖最多会拆出\(O(\log n)\)的区间，和前面的复杂度相同，再加上\(set\)和树状数组，时间复杂度应该是\(O(n\log^2 n)\)（大概没算错？）

//minamoto
#include<bits/stdc++.h>
#define R register
#define IT set<node>::iterator
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
using namespace std;
char buf[1<<21],*p1=buf,*p2=buf;
inline char getc(){return p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++;}
int read(){
    R int res,f=1;R char ch;
    while((ch=getc())>'9'||ch<'0')(ch=='-')&&(f=-1);
    for(res=ch-'0';(ch=getc())>='0'&&ch<='9';res=res*10+ch-'0');
    return res*f;
}
int read(char *s){
	R int len=0;R char ch;while(((ch=getc())>'z'||ch<'a'));
	for(s[++len]=ch;(ch=getc())>='a'&&ch<='z';s[++len]=ch);
	return s[len+1]='\0',len;
}
char sr[1<<21],z[20];int C=-1,Z=0;
inline void Ot(){fwrite(sr,1,C+1,stdout),C=-1;}
void print(R int x){
    if(C>1<<20)Ot();if(x<0)sr[++C]='-',x=-x;
    while(z[++Z]=x%10+48,x/=10);
    while(sr[++C]=z[Z],--Z);sr[++C]='\n';
}
const int N=5e5+5;
struct node{
	int l,r,c;
	node(){}
	node(R int ll,R int rr=-1,R int cc=N){l=ll,r=rr,c=cc;}
	inline bool operator <(const node &b)const{return l<b.l;}
};set<node>pool[N],*s[N];
struct eg{int v,nx;}e[N<<1];int head[N],tot;char t[25];
int dfn[N],sz[N],son[N],fa[N],top[N],dep[N],bg[N],c[N],mx[N];
int n,m,cnt,tim,las;
inline void add(R int u,R int v){e[++tot]={v,head[u]},head[u]=tot;}
inline void upd(R int x,R int y){for(;x<N;x+=x&-x)c[x]+=y;}
inline int ask(R int x){R int res=0;for(;x;x-=x&-x)res+=c[x];return res;}
IT split(set<node> *s,int pos){
	IT it=s->lower_bound(node(pos));
	if(it!=s->end()&&it->l==pos)return it;
	--it;int l=it->l,r=it->r,c=it->c;
	s->erase(it),s->insert(node(l,pos-1,c));
	return s->insert(node(pos,r,c)).first;
}
void ins(set<node> *s,int l,int r,int c){
	IT itr=split(s,r+1),itl=split(s,l);
	for(IT it=itl;it!=itr;++it)upd(it->c,-(it->r-it->l+1));
	upd(c,r-l+1);
	s->erase(itl,itr),s->insert(node(l,r,c));
}
void dfs1(int u){
	sz[u]=1,dep[u]=dep[fa[u]]+1;
	go(u)if(v!=fa[u]){
		fa[v]=u,dfs1(v),sz[u]+=sz[v];
		sz[v]>sz[son[u]]?son[u]=v:0;
	}
}
void dfs2(int u,int t){
	top[u]=t,mx[u]=dfn[u]=++cnt;
	if(son[u])dfs2(son[u],t),cmax(mx[u],mx[son[u]]);
	if(u==t)s[u]=&pool[u],s[u]->insert(node(dfn[u],mx[u]+1));
	go(u)if(!top[v])dfs2(v,v);
}
int LCA(int u,int v){
	while(top[u]!=top[v]){
		if(dep[top[u]]<dep[top[v]])swap(u,v);
		u=fa[top[u]];
	}
	return dep[u]<dep[v]?u:v;
}
inline int dis(R int u,R int v){return dep[u]+dep[v]-(dep[LCA(u,v)]<<1)+1;}
void update(int u,int v){
	bg[++tim]=u;
	while(top[u]!=top[v]){
		if(dep[top[u]]<dep[top[v]])swap(u,v);
		ins(s[top[u]],dfn[top[u]],dfn[u],tim);
		u=fa[top[u]];
	}
	if(dep[u]>dep[v])swap(u,v);
	ins(s[top[u]],dfn[u],dfn[v],tim);
}
int query(int u){
	int c=split(s[top[u]],dfn[u])->c;
	return ask(c-1)+dis(u,bg[c]);
}
int main(){
//	freopen("testdata.in","r",stdin);
	n=read(),m=read();
	for(R int i=1,u,v;i<n;++i)u=read(),v=read(),add(u,v),add(v,u);
	dfs1(1),dfs2(1,1),las=n;
	fp(i,1,n-1)update(i,i+1);
	for(R int T=1,u,v;T<=m;++T){
		read(t),u=read(),t[1]=='c'?v=read():0;
		switch(t[1]){
			case 'u':update(las,u),las=u;break;
			case 'w':print(query(u));break;
			case 'c':print(query(u)<query(v)?u:v);break;
		}
	}
	return Ot(),0;
}

upd：为了卡常改了改代码，下面这份已经不能看了（然而还是被写\(LCT\)的聚聚们吊起来打）

下面这个加了一点优化，具体就是

1.一开始的时候不暴力\(up\)，从大到小染色，那么每个点最多只会被染色一次

2.区间推倒……啊呸推平的时候判一下左右端点是不是刚好卡到边界（不过并没有什么卵用就是了）

//minamoto
#include<bits/stdc++.h>
#define R register
#define IT set<node>::iterator
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
using namespace std;
char buf[1<<21],*p1=buf,*p2=buf;
inline char getc(){return p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++;}
int read(){
    R int res,f=1;R char ch;
    while((ch=getc())>'9'||ch<'0')(ch=='-')&&(f=-1);
    for(res=ch-'0';(ch=getc())>='0'&&ch<='9';res=res*10+ch-'0');
    return res*f;
}
inline char getop(){R char ch;while((ch=getc())>'z'||ch<'a');return ch;}
char sr[1<<21],z[20];int C=-1,Z=0;
inline void Ot(){fwrite(sr,1,C+1,stdout),C=-1;}
void print(R int x){
    if(C>1<<20)Ot();if(x<0)sr[++C]='-',x=-x;
    while(z[++Z]=x%10+48,x/=10);
    while(sr[++C]=z[Z],--Z);sr[++C]='\n';
}
const int N=5e5+5;
struct node{
    int l,r,c;
    node(){}
    node(R int ll,R int rr=-1,R int cc=N){l=ll,r=rr,c=cc;}
    inline bool operator <(const node &b)const{return l<b.l;}
};set<node>pool[N],*s[N];
struct eg{int v,nx;}e[N<<1];int head[N],tot;char op;
int dfn[N],sz[N],son[N],fa[N],top[N],dep[N],bg[N],c[N],mx[N],ga[N],col[N];
int n,m,cnt,tim,las,lim,num;
inline void add(R int u,R int v){e[++tot]={v,head[u]},head[u]=tot;}
inline void upd(R int x,R int y){for(;x<lim;x+=x&-x)c[x]+=y;}
inline int ask(R int x){R int res=0;for(;x;x-=x&-x)res+=c[x];return res;}
inline int find(int x){return ga[x]==x?x:ga[x]=find(ga[x]);}
inline set<node> *newnode(){return &pool[++num];}
IT split(set<node> *s,int pos){
    IT it=s->lower_bound(node(pos));
    if(it!=s->end()&&it->l==pos)return it;
    --it;int l=it->l,r=it->r,c=it->c;
    s->erase(it),s->insert(node(l,pos-1,c));
    return s->insert(node(pos,r,c)).first;
}
void ins(set<node> *s,int l,int r,int id,int c){
	upd(c,r-l+1);
	if(l==dfn[id]&&r==mx[id]){
		for(IT it=s->begin();it!=s->end();++it)upd(it->c,-(it->r-it->l+1));
		s->erase(s->begin(),s->end()),s->insert(node(l,r,c));
		return;
	}
	if(l==dfn[id]){
		IT itr=split(s,r+1);
		for(IT it=s->begin();it!=itr;++it)upd(it->c,-(it->r-it->l+1));
		s->erase(s->begin(),itr),s->insert(node(l,r,c));
		return;
	}
	if(r==mx[id]){
		IT itl=split(s,l);
		for(IT it=itl;it!=s->end();++it)upd(it->c,-(it->r-it->l+1));
		s->erase(itl,s->end()),s->insert(node(l,r,c));
		return;
	}
	IT itr=split(s,r+1),itl=split(s,l);
	for(IT it=itl;it!=itr;++it)upd(it->c,-(it->r-it->l+1));
	s->erase(itl,itr),s->insert(node(l,r,c));
}
void dfs1(int u){
    sz[u]=1,dep[u]=dep[fa[u]]+1;
    go(u)if(v!=fa[u]){
        fa[v]=u,dfs1(v),sz[u]+=sz[v];
        sz[v]>sz[son[u]]?son[u]=v:0;
    }
}
void dfs2(int u,int t){
    top[u]=t,mx[u]=dfn[u]=++cnt;
    if(son[u])dfs2(son[u],t),cmax(mx[u],mx[son[u]]);
    if(u==t)s[u]=newnode();
    go(u)if(!top[v])dfs2(v,v);
}
void dfs3(int u,int t,int mn){
	if(!son[u]||col[son[u]]!=col[mn])s[t]->insert(node(dfn[mn],dfn[u],col[u])),upd(col[u],dfn[u]-dfn[mn]+1);
	if(son[u])dfs3(son[u],t,col[mn]==col[son[u]]?mn:son[u]);
	go(u)if(v!=fa[u]&&v!=son[u])dfs3(v,v,v);
}
int LCA(int u,int v){
    while(top[u]!=top[v]){
        if(dep[top[u]]<dep[top[v]])swap(u,v);
        u=fa[top[u]];
    }
    return dep[u]<dep[v]?u:v;
}
inline int dis(R int u,R int v){return dep[u]+dep[v]-(dep[LCA(u,v)]<<1)+1;}
void update(int u,int v){
    bg[++tim]=u;
    while(top[u]!=top[v]){
        if(dep[top[u]]<dep[top[v]])swap(u,v);
        ins(s[top[u]],dfn[top[u]],dfn[u],top[u],tim);
        u=fa[top[u]];
    }
    if(dep[u]>dep[v])swap(u,v);
    ins(s[top[u]],dfn[u],dfn[v],top[u],tim);
}
int query(int u){
    int c=split(s[top[u]],dfn[u])->c;
    return ask(c-1)+dis(u,bg[c]);
}
void build(int u,int v,int c){
	int lca=LCA(u,v);
	bg[c]=u,u=find(u),v=find(v);
	while(u!=v){
		if(dep[u]<dep[v])swap(u,v);
		col[u]=c,ga[u]=find(fa[u]),u=ga[u];
	}
	if(!u)return;
	u==lca?(col[u]=c,ga[u]=find(fa[u])):0;
}
int main(){
//	freopen("testdata.in","r",stdin);
    n=read(),m=read(),lim=n+m;
    for(R int i=1,u,v;i<n;++i)u=read(),v=read(),add(u,v),add(v,u);
    dfs1(1),dfs2(1,1),las=tim=n;
	fp(i,1,n){
		ga[i]=i;
		if(son[fa[i]]!=i)s[i]=&pool[i];
	}
	fd(i,n-1,1)build(i,i+1,i+1);
	dfs3(1,1,1);
    for(R int T=1,u,v;T<=m;++T){
        op=getop(),u=read(),op=='c'?v=read():0;
        switch(op){
            case 'u':update(las,u),las=u;break;
            case 'w':print(query(u));break;
            case 'c':print(query(u)<query(v)?u:v);break;
        }
    }
    return Ot(),0;
}