Deep Learning 学习笔记（5）：Regularization 规则化

过拟合（overfitting）：

实际操作过程中，无论是线性回归还是逻辑回归，其假设函数h(x)都是人为设定的（尽管可以通过实验选择最优）。

这样子就可能出线“欠拟合”或者“过拟合”现象。

所谓过拟合，就是模型复杂度过高，模型很好地拟合了训练样本却对未知样本的预测能力不足。（亦称"泛化"能力不足）

所谓欠拟合，就是模型复杂度过低，模型不能很好拟合不管是训练样本还是其他样本。

例子：

如果输出与输入大致成二次关系，

那么我们用一次函数去拟合，拟合结果过于平缓，跟不上变化，这就是“欠拟合”

用3、4次函数去拟合，则会出现过多的“抖动”，这就是“过拟合”

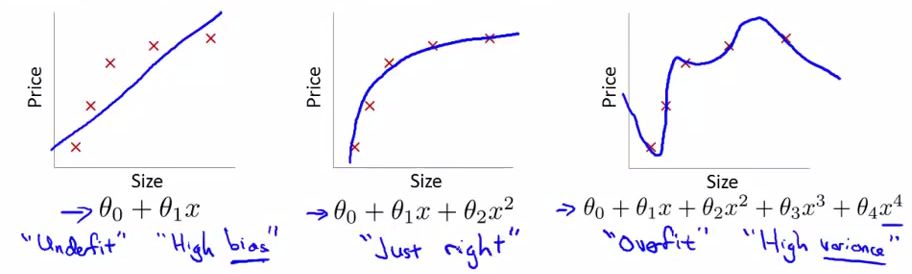
如图，

线性回归中的“欠拟合”和“过拟合”，可见"欠拟合"不能贴近数据的变化，而"过拟合"产生了过多的"抖动"

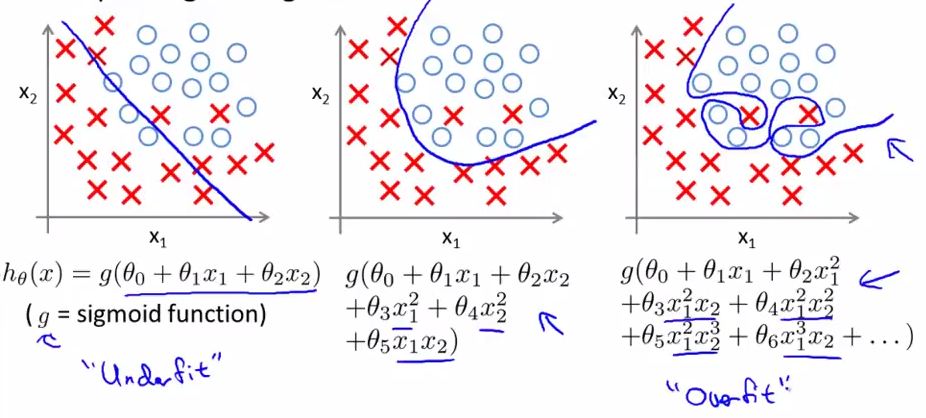
逻辑回归中的“欠拟合”和“过拟合”，“欠拟合”不能很好的进行分类，“过拟合”则过多地受到特例的影响，不能给出具有良好泛化能力的方程

实际操作当中，由于过拟合的影响可以通过增大训练数据量来减轻，和正则化

所以一般建模宁over不under。

---

Regularization（正则化）：

正则化希望在代价函数中增加惩罚项来减少过拟合项的系数的大小，以减少过拟合项的影响。

惩罚因子  ：

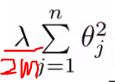（好难看……）

修改后的代价函数：

线性：

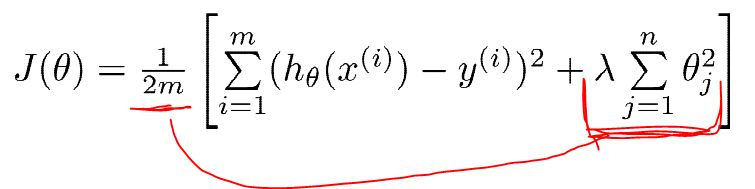
逻辑：

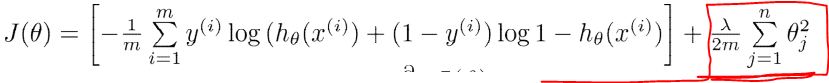
　　*用本专业的知识可以这么理解：对于一个模型，我们希望尽量用低次函数拟合得到良好效果，尽量少用高次函数（高频抖动囧rz）。

　　　如果一个模型欠拟合，其前面的cost会过高；如果一个函数过拟合，高次函数系数较大，后面的正则惩罚项的cost又会过高。

　　　所以学习过程会自动平衡模型的复杂程度，得到一个对训练样本和未知样本都能良好拟合的模型。（当然得调参）

然后用修改后的代价方程进行梯度下降的计算即可（加多了一项，偏导很容易算吧）

注意：常数项的系数我们并不进行“惩罚”，所以常数项的偏导与其他项的偏导计算有些许不同。