POJ 1191 棋盘分割 【DFS记忆化搜索经典】

题目传送门：http://poj.org/problem?id=1191

棋盘分割

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 16150		Accepted: 5768

Description

将一个８*８的棋盘进行如下分割：将原棋盘割下一块矩形棋盘并使剩下部分也是矩形，再将剩下的部分继续如此分割，这样割了(n-1)次后，连同最后剩下的矩形棋盘共有n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行) 

原棋盘上每一格有一个分值，一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成n块矩形棋盘，并使各矩形棋盘总分的均方差最小。 
均方差 

其中平均值 
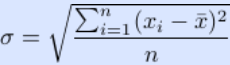
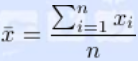
x_i为第i块矩形棋盘的总分。 
请编程对给出的棋盘及n，求出O'的最小值。 

Input

第1行为一个整数n(1 < n < 15)。 
第2行至第9行每行为8个小于100的非负整数，表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。 

Output

仅一个数，为O'（四舍五入精确到小数点后三位）。

Sample Input

3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3

Sample Output

1.633

Source

Noi 99

 

题意概括：

中文题，不容小觑。

解题思路：

一、DFS搜索，每次分割棋盘可以选择两个方向 横切（改变Y的范围） 或者 竖切（改变X的范围）；选择切割方向之后需要选择舍弃两部分之中的其中一部分，继续DFS另一部分。

二、但单纯的搜索太慢，我们可以发现其实是因为有很多子问题重叠，所以不妨用一个四维数组记录每次小矩形的运算结果，数组下标为小矩阵左上角和右下角的坐标。

三、公式化简：

 

AC code：

 ///POJ 1191 棋盘分割 （记忆化搜索经典）
 #include <cstdio>
 #include <iostream>
 #include <algorithm>
 #include <cstring>
 #include <cmath>
 #define INF 0x3f3f3f3f
 #define ll long long int
 #define mod 1000000007
 using namespace std;
 
 const int MAXN = ;
 const int MAXM = ;
 double d[MAXN][MAXM][MAXM][MAXM][MAXM];
 double record[MAXM][MAXM][MAXM][MAXM];
 double mmp[MAXM][MAXM];
 double sum, ave;
 int N;
 
 double get_sum(int x1, int y1, int x2, int y2)
 {
     if(record[x1][y1][x2][y2]>=) return record[x1][y1][x2][y2];
     double re = ;
     for(int i = x1; i <= x2; i++)
     for(int j = y1; j <= y2; j++)
             re+=mmp[i][j];
     record[x1][y1][x2][y2] = re*re;
     return record[x1][y1][x2][y2];
 }
 
 double dfs(int x1, int y1, int x2, int y2, int cnt)
 {
     if(d[cnt][x1][y1][x2][y2]>=) return d[cnt][x1][y1][x2][y2];
     if(cnt == N)
     {
         return get_sum(x1, y1, x2, y2);
     }
     double min_sum = ;
     double tp = ;
     for(int i = x1; i < x2; i++)
     {
         tp = get_sum(x1, y1, i, y2) + dfs(i+, y1, x2, y2, cnt+);
         if(min_sum > tp) min_sum = tp;
         tp = get_sum(i+, y1, x2, y2) + dfs(x1, y1, i, y2, cnt+);
         if(min_sum > tp) min_sum = tp;
     }
     for(int j = y1; j < y2; j++)
     {
         tp = get_sum(x1, y1, x2, j) + dfs(x1, j+, x2, y2, cnt+);
         if(min_sum > tp) min_sum = tp;
         tp = get_sum(x1, j+, x2, y2) + dfs(x1, y1, x2, j, cnt+);
         if(min_sum > tp) min_sum = tp;
     }
     d[cnt][x1][y1][x2][y2] = min_sum;
     return min_sum;
 }
 
 int main()
 {
     scanf("%d", &N);
     memset(d, -, sizeof(d));
     memset(record, -, sizeof(record));
     for(int i = ; i <= ; i++)
     for(int j = ; j <= ; j++)
     {
         scanf("%lf", &mmp[i][j]);
         sum+=mmp[i][j];
     }
     ave = sum/(N*1.0);
     ave*=ave;
     double res = dfs(, , , , );
     double ans = sqrt(res/N-ave);
     printf("%.3f\n", ans);
     return ;
 }