POJ 2007--Scrambled Polygon(计算凸包，点集顺序)

Scrambled Polygon

Time Limit: 1000MS		Memory Limit: 30000K
Total Submissions: 10094		Accepted: 4765

Description

A closed polygon is a figure bounded by a finite number of line segments. The intersections of the bounding line segments are called the vertices of the polygon. When one starts at any vertex of a closed polygon and traverses each bounding line segment exactly once, one comes back to the starting vertex.

A closed polygon is called convex if the line segment joining any two points of the polygon lies in the polygon. Figure 1 shows a closed polygon which is convex and one which is not convex. (Informally, a closed polygon is convex if its border doesn't have any "dents".)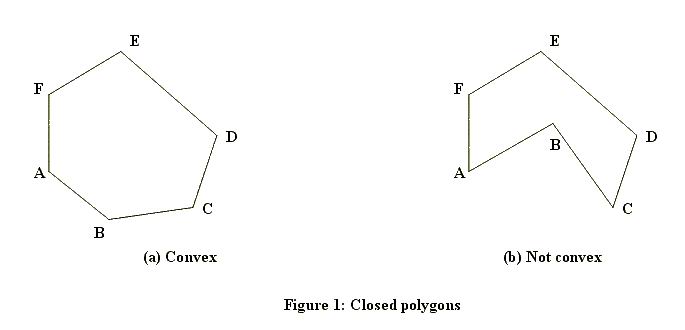 

The subject of this problem is a closed convex polygon in the coordinate plane, one of whose vertices is the origin (x = 0, y = 0). Figure 2 shows an example. Such a polygon will have two properties significant for this problem.

The first property is that the vertices of the polygon will be confined to three or fewer of the four quadrants of the coordinate plane. In the example shown in Figure 2, none of the vertices are in the second quadrant (where x < 0, y > 0).

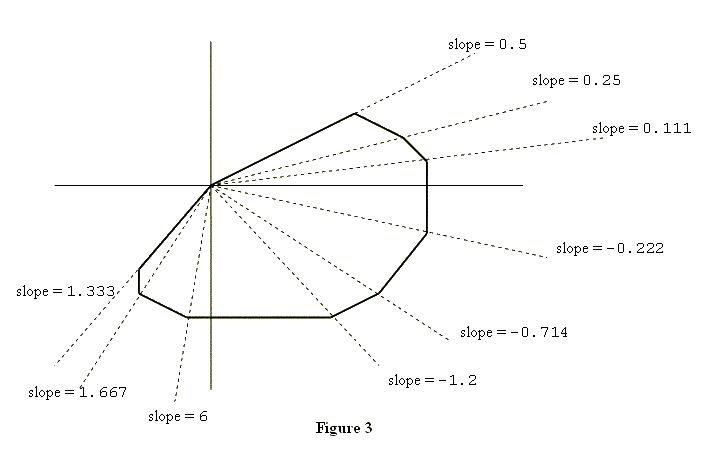
To describe the second property, suppose you "take a trip" around the polygon: start at (0, 0), visit all other vertices exactly once, and arrive at (0, 0). As you visit each vertex (other than (0, 0)), draw the diagonal that connects the current vertex with (0, 0), and calculate the slope of this diagonal. Then, within each quadrant, the slopes of these diagonals will form a decreasing or increasing sequence of numbers, i.e., they will be sorted. Figure 3 illustrates this point.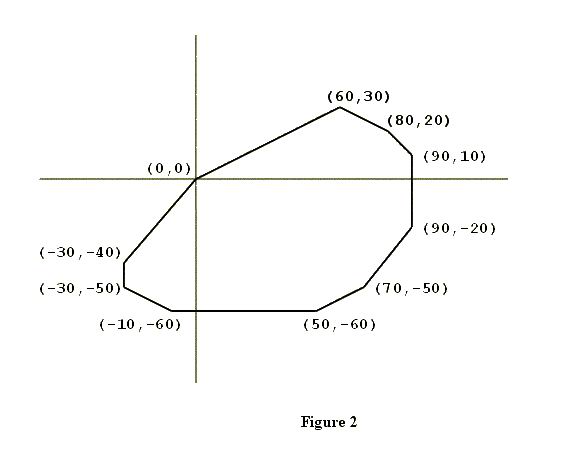 
 

Input

The input lists the vertices of a closed convex polygon in the plane. The number of lines in the input will be at least three but no more than 50. Each line contains the x and y coordinates of one vertex. Each x and y coordinate is an integer in the range -999..999. The vertex on the first line of the input file will be the origin, i.e., x = 0 and y = 0. Otherwise, the vertices may be in a scrambled order. Except for the origin, no vertex will be on the x-axis or the y-axis. No three vertices are colinear.

Output

The output lists the vertices of the given polygon, one vertex per line. Each vertex from the input appears exactly once in the output. The origin (0,0) is the vertex on the first line of the output. The order of vertices in the output will determine a trip taken along the polygon's border, in the counterclockwise direction. The output format for each vertex is (x,y) as shown below.

Sample Input

0 0
70 -50
60 30
-30 -50
80 20
50 -60
90 -20
-30 -40
-10 -60
90 10

Sample Output

(0,0)
(-30,-40)
(-30,-50)
(-10,-60)
(50,-60)
(70,-50)
(90,-20)
(90,10)
(80,20)
(60,30)

Source

Rocky Mountain 2004

 

这道题用卷包裹法过不去啊，仔细看题发现要逆时针输出，于是换成扫描法就过了。。。Orz

Graham求完的凸包点集依次出栈可以得到从起点开始顺时针旋转的所有凸包上的点。

 

 #include<iostream>
 #include<algorithm>
 #include<cmath>
 #include<cstdio>
 using namespace std;
 const int maxn = ;
 typedef struct point {
     double x, y;
     point() {

     }
     point(double a, double b) {
         x = a;
         y = b;
     }
     point operator -(const point &b) const{
         return point(x - b.x, y - b.x);
     }
     double operator *(const point &b)const {
         return x*b.x + y*b.y;
     }
 }point;
 point p[maxn];
 int n=, res[maxn];
 int top;//top模拟栈顶
 bool cmp(point a, point b) {
     if (a.y == b.y)    return a.x < b.x;
     return a.y < b.y;
 }
 bool multi(point p1, point p2, point p0) {  //判断p1p0和p2p0的关系，<0,p1p0在p2p0的逆时针方向,>0,p1p0在p2p0的顺时针方向
     return (p1.x - p0.x)*(p2.y - p0.y) >= (p2.x - p0.x)*(p1.y - p0.y);
 }
 void Graham(){
     int i, len;//top模拟栈顶
     sort(p, p + n, cmp);
     top = ;
     //少于3个点也就没有办法形成凸包
     if (n == )return; res[] = ;
     if (n == )return; res[] = ;
     if (n == )return; res[] = ;
     for (i = ;  i < n; i++) {
         while (top&&multi(p[i], p[res[top]], p[res[top - ]]))    //如果当前这个点和栈顶两个点构成折线右拐了，就回溯到上一个点
             top--;                                                //弹出栈顶
         res[++top] = i;                                            //否则将这个点入栈
     }
     len = top;
     res[++top] = n - ;
     for (i = n - ; i >= ; i--) {
         while (top!=len&&multi(p[i], p[res[top]], p[res[top - ]]))
             top--;
         res[++top] = i;
     }
 }
 int main(void) {
     int i, s;//s为起点坐标
     while (scanf("%lf%lf", &p[n].x, &p[n].y)!=EOF)n++;
     Graham();
     for (s = ; s < top; s++) {
         if (!p[res[s]].x && !p[res[s]].y)    //找到原点
             break;
     }
     for (i = s; i < top; i++) {
         printf("(%.lf,%.lf)\n",p[res[i]].x, p[res[i]].y);
     }
     for (i = ; i < s; i++) {
         printf("(%.lf,%.lf)\n", p[res[i]].x, p[res[i]].y);
     }
     return ;
 }