2017-11-4—稳态和暂态/瞬态(对运放积分电路的思考)[待仿真]
先直接截图了,暂态或者说瞬态都是暂时的状态,是从一个稳定态到另一个稳定态的过程。
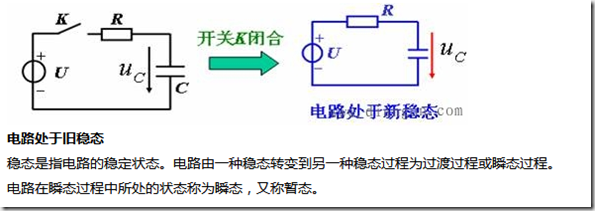
之所以要了解这个概念是因为对于使用运放搭建的模拟PID有很多的疑惑,比如负反馈没有电阻满不满足“虚短”原则?
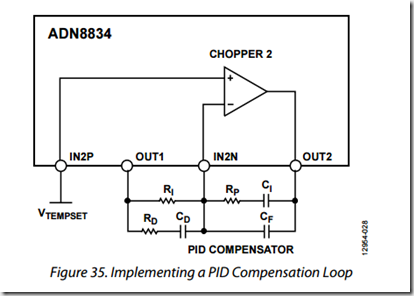
网上的答案大多都是按照已经满足“虚短”“虚断”原则下进行分析的,包括积分电路也是如此。

积分电路
如果Vi保持正值,Vo输出为0,这个电路就是一个比较器,电容两端电压固定。这么分析的话跟积分半毛钱关系都没有啊。。。
积分的过程只能是发生在瞬态/暂态(充放电的过程),那瞬态/暂态(充放电的过程)的时候如何确定运放的同相输入端和反相输入端电压相等呢?
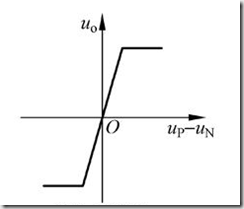
运放输入输出特性曲线
轨对轨运放判断负反馈的时候,只要Vout不为上限两个电源轨对应的电压值,就认为其满足“虚短”“虚断”原则。
那积分电路能保证暂态/瞬态的时候Vout不为电源轨的电压吗?
先假设Vin固定,Vout为正电源值,如果是稳态,则电容两端电压为Vout-Vin压差;Qc=C*Uc,
Vin抬高,但是不高于同相输入端电压,Vout的下一个稳态还是输出正电源轨,Vc电量流失,压降下降!但是Vout不会变!!
Vin从低于同相输入端抬高到还是低于同向输入端的过程中应该都不满足“虚短”,Vout也始终处于特性曲线的正饱和区。。
Vin继续抬高,直到略低于同相输入端电压的时候,这回肯定会进入特性曲线的线性放大区。。只有这会的电容充放电才会反映到Vout!!!
才能真正体现积分的作用!!!!!
那么又回到积分电路,积分电路里面的R1太大的话积分效果应该非常的慢!!!

总结:积分电路体现在非常小的一段区间内!!
需要进一步使用LTspice仿真验证。。
2017-11-4—稳态和暂态/瞬态(对运放积分电路的思考)[待仿真]的更多相关文章
- 【小白的CFD之旅】24 稳态和瞬态
小白最近在练习案例的时候,对稳态和瞬态的问题,产生了一些疑问.譬如说,为什么有的案例用稳态,而有的案例用瞬态?有时候相同的案例既可以用稳态也可以用瞬态,而有的案例却只能用瞬态计算?小白决定找小牛师兄问 ...
- 基于SimpleChain Beta的跨链交互与持续稳态思考
1. 区块链扩展性迷局 比特币作为第一个区块链应用与运行到目前为止最被信任的公链,其扩展性问题却持续被作为焦点贯穿着整个链的发展周期.事实上,在2009年1月4日比特币出现的那一天到2010年10月1 ...
- [Fundamental of Power Electronics]-PART I-2.稳态变换器原理分析-2.2 伏秒平衡/安秒平衡 小纹波近似
2.2 电感伏秒平衡.电容充放电平衡以及小纹波近似 让我们更加仔细地观察图2.6中的buck变换器的电感和电容的波形.我们是不可能设计一个滤波器能够只允许直流分量通过而完全滤除开关频率次谐波的.所以, ...
- [Fundamental of Power Electronics]-PART I-3.稳态等效电路建模,损耗和效率-3.1 直流变压器模型
3.1 直流变压器模型 如图3.1所示,任何开关变换器都包含三个部分:功率输入,功率输出以及控制输入.输入功率按控制输入进行特定的功率变换输出到负载.理想情况下,这些功能将以100%的效率完成,因此 ...
- Chapter 2 简单DC-DC变换器稳态分析小结
Chapter 2 简单DC-DC变换器稳态分析小结 1 本章重点 1.1 小纹波近似 所谓小纹波近似就是DC-DC变换器的稳态分析中,假定开关频率次的纹波相对于直流分量而言非常小,可以将其忽略进行各 ...
- [家里蹲大学数学杂志]第033期稳态可压Navier-Stokes方程弱解的存在性
1. 方程 考虑 $\bbR^3$ 中有界区域 $\Omega$ 上如下的稳态流动: $$\bee\label{eq} \left\{\ba{ll} \Div(\varrho\bbu)=0,\\ \ ...
- 一种全新的MEMS开关——高性能、快速、低能耗以及双稳态
这种开关最早由申军教授和研究生阮梅春发明,研究生埃里克·朗格卢瓦在简化结构和缩小尺寸上作了探索,黄志林用相同原理做出了MEMS光学镜子开关,曹志良改变设计.材料和工艺后制作出了能同步开关的矩阵.这种M ...
- [LOJ 6249]「CodePlus 2017 11 月赛」汀博尔
Description 有 n 棵树,初始时每棵树的高度为 H_i,第 i 棵树每月都会长高 A_i.现在有个木料长度总量为 S 的订单,客户要求每块木料的长度不能小于 L,而且木料必须是整棵树(即不 ...
- [LOJ 6248]「CodePlus 2017 11 月赛」晨跑
Description “无体育,不清华”.“每天锻炼一小时,健康工作五十年,幸福生活一辈子” 在清华,体育运动绝对是同学们生活中不可或缺的一部分.为了响应学校的号召,模范好学生王队长决定坚持晨跑.不 ...
随机推荐
- vue实战记录(二)- vue实现购物车功能之创建vue实例
vue实战,一步步实现vue购物车功能的过程记录,课程与素材来自慕课网,自己搭建了express本地服务器来请求数据 作者:狐狸家的鱼 本文链接:vue实战-实现购物车功能(二) GitHub:sue ...
- BSGS与扩展BSGS
BSGS \(BSGS\)算法又称大步小步\((Baby-Step-Giant-Step)\)算法 \(BSGS\)算法主要用于解以下同余方程 \[A^x\equiv B(mod\ p)\]其中\(( ...
- Python【pyyaml】模块
pyyaml模块安装: pip install pyyaml pyyaml导入: import yaml pyyaml使用: 1.使用前,在pycharm中新建一个以yaml或yml结尾的文件,保存为 ...
- 【ASP.NET】website转webapplication
*以下操作都以VS2013为参考: #新建两种web项目 1.添加webapplication项目: 2.添加website项目: #比较两种web项目新建的webform页面的不同点: 1.文件目录 ...
- LFYZ-OJ ID: 1024 火车站
火车过站 问题描述 火车从始发站(称为第1站)开出,在始发站上车的人数为a,然后到达第2站,在第2站有人上.下车,但上.下车的人数相同,因此在第2站开出时(即在到达第3站之前)车上的人数保持为a人.从 ...
- expprt与环境变量
一.Windows 环境变量 1.在Windows 系统下,很多软件安装都需要配置环境变量,比如 安装 jdk ,如果不配置环境变量,在非软件安装的目录下运行javac 命令,将会报告找不到文件,类似 ...
- Node.js实战项目学习系列(5) node基础模块 path
前言 前面已经学习了很多跟Node相关的知识,譬如开发环境.CommonJs,那么从现在开始要正式学习node的基本模块了,开始node编程之旅了. path path 模块提供用于处理文件路径和目录 ...
- docker学习-----docker服务的安装
docker 以下观点个人理解,只做参考 一.docker本身的优势 1.docker他本身是一个容器,用来方便我们项目打包,做服务器虚拟化,统一开发者环境等多种优势:运行于docker上的项目可以快 ...
- 修改WEB项目的发布名称
1.在要修改的项目上单击右键选择properties,修改web选项中的Web Context-root中的发布名称即可,但需要注意的是修改发布名称后需要将项目从服务器中先移除后再重新添加.
- Python3:判断三角形的类型
# 判断三角形类型def triangle(a,b,c): if a>0 and b>0 and c>0: if a+b>c and b+c>a and a+c>b ...
