S0.3 直方图

目录

• 直方图（一）
  • 直方图概念
  • 直方图分类
  • 直方图优点
  • 直方图应用
  • opencv3直方图产生函数cvCalcHist()
  • 画图函数
  • 完整示例

直方图（一）

直方图概念

直方图是图像中像素强度分布的图形表达方式.

它统计了每一个强度值所具有的像素个数.

直方图分类

灰度直方图：边缘检测

RGB直方图：图像检索

二维直方图

直方图优点

计算代价低。

具有图像平移、缩放、旋转的不变性。

图像分割是图像识别的基础，基于灰度直方图的阈值分割计算简单，对遥感图像处理效果好。

• 直方图是计算机视觉最经典的工具之一。

直方图应用

• 图像相似度
• 灰度图像的阈值分割（将来会写一篇博客讲这个）
• 基于颜色的图像检索
• 图像分类

ps:喜欢摄影的朋友一定知道直方图可以做照片的后期处理，调出影调风格。

opencv3直方图产生函数cvCalcHist()

经过这个函数会得到一个Mat

void calcHist(
    const Mat* images,
    int nimages,
    const int* channels,
    InputArray mask,
    OutputArray hist,
    int dims,
    const int* histSize,
    const float** ranges,
    bool uniform=true,
    bool accumulate=false
)

const Mat* images：为输入图像的指针。

int nimages：要计算直方图的图像的个数。此函数可以为多图像求直方图，我们通常情况下都只作用于单一图像，所以通常nimages=1。

const int* channels：图像的通道，它是一个数组，如果是灰度图像则channels[1]={0};如果是彩色图像则channels[3]={0,1,2}；如果是只是求彩色图像第2个通道的直方图，则channels[1]={1};

IuputArray mask：是一个遮罩图像用于确定哪些点参与计算，实际应用中是个很好的参数，默认情况我们都设置为一个空图像，即：Mat()。

OutArray hist：计算得到的直方图

int dims：得到的直方图的维数，灰度图像为1维，彩色图像为3维。

const int* histSize：直方图横坐标的区间数。如果是10，则它会横坐标分为10份，然后统计每个区间的像素点总和。

const float** ranges：这是一个二维数组，用来指出每个区间的范围。

后面两个参数都有默认值，uniform参数表明直方图是否等距，最后一个参数与多图像下直方图的显示与存储有关。

画图函数

Mat getHistImg(const MatND& hist)
{
    double maxVal=0;
    double minVal=0;

    //找到直方图中的最大值和最小值
    minMaxLoc(hist,&minVal,&maxVal,0,0);
    int histSize=hist.rows;
    Mat histImg(histSize,histSize,CV_8U,Scalar(255));
    // 设置最大峰值为图像高度的90%
    int hpt=static_cast<int>(0.9*histSize);

    for(int h=0;h<histSize;h++)
    {
        float binVal=hist.at<float>(h);
        int intensity=static_cast<int>(binVal*hpt/maxVal);
        line(histImg,Point(h,histSize),Point(h,histSize-intensity),Scalar::all(0));
    }

    return histImg;
}

完整示例

示例

#include <opencv2/highgui/highgui.hpp>
#include <opencv2/imgproc/imgproc.hpp>
#include <opencv2/core/core.hpp>
using namespace cv;

Mat getHistImg(const MatND& hist)
{
    double maxVal=0;
    double minVal=0;

    //找到直方图中的最大值和最小值
    minMaxLoc(hist,&minVal,&maxVal,0,0);
    int histSize=hist.rows;
    Mat histImg(histSize,histSize,CV_8U,Scalar(255));
    // 设置最大峰值为图像高度的90%
    int hpt=static_cast<int>(0.9*histSize);

    for(int h=0;h<histSize;h++)
    {
        float binVal=hist.at<float>(h);
        int intensity=static_cast<int>(binVal*hpt/maxVal);
        line(histImg,Point(h,histSize),Point(h,histSize-intensity),Scalar::all(0));
    }

    return histImg;
}

int main()
{
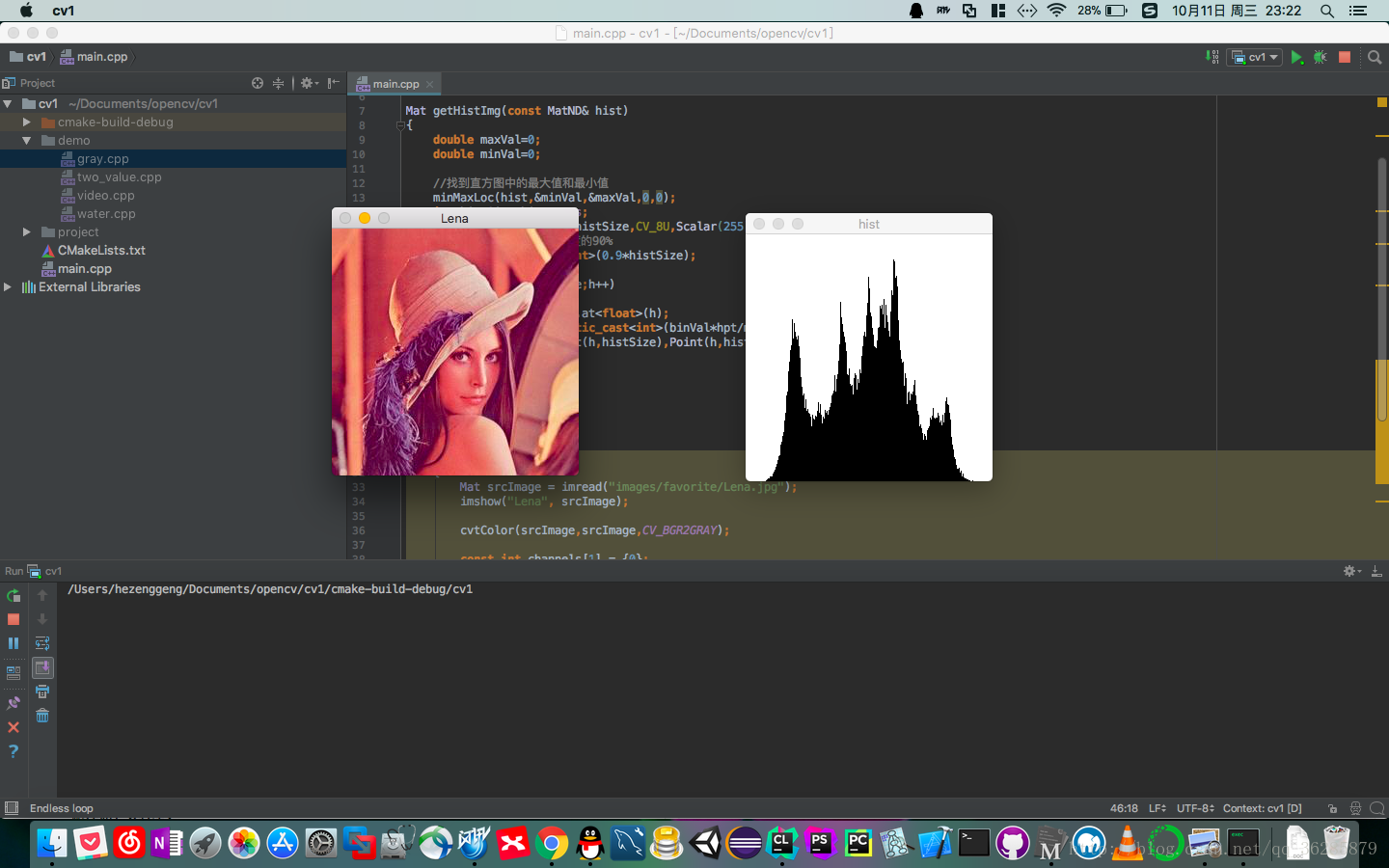
    Mat srcImage = imread("images/favorite/Lena.jpg");
    imshow("Lena", srcImage);
    cvtColor(srcImage,srcImage,CV_BGR2GRAY);

    const int channels[1] = {0};
    const int histSize[1] = {256};
    float hranges[2]={0,255};
    const float* ranges[1]={hranges};
    MatND hist; //相当于mat
    calcHist(&srcImage,1,channels,Mat(),hist,1,histSize,ranges);

    imshow("hist", getHistImg(hist));
    waitKey(10000);

    return 0;
}