1. void resetNumA(string numAStr);
  2. //使用string重置numB
  3. void resetNumB(string numBStr);
  4. //将数组转换为字符串，用于输出
  5. string getNumString(int* num);
  6. //判断两个数字哪个大
  7. int compare(string numAStr, string numBStr);
  8. //加法
  9. string sum(string numAStr, string numBStr);
  10. //减法
  11. string sub(string numAStr, string numBStr);
  12. //乘法
  13. string mul(string numAStr, string numBStr);
  14. //除
  15. string div(string numAStr, string numBStr);
  16. //取余
  17. string mod(string numAStr, string numBStr);
  18. //模幂算法
  19. string getMod(string m, string pow, string n);
  20. //求2的n次方函数
  21. string mul_2(int i);
  22. //求m的n次方
  23. string mul_m(string m, string n);
  24. #endif
  1. #include<iostream>
  2. #include"operation.h"
  3. #include<string>
  4. #include<vector>
  5. using namespace std;
  6.  
  7. //结果支持的最大位数
  8. const static int M = ;
  9.  
  10. int numA[M];
  11. int numB[M];
  12.  
  13. //使用string重置numA
  14. void resetNumA(string numAStr)
  15. {
  16.     memset(numA, , M * sizeof(int));
  17.  
  18.     //将字符串的每一位都转换成数字传入数组
  19.     for (int i = ; i < numAStr.length(); i++)
  20.     {
  21.         numA[i] = numAStr[numAStr.length() - i - ] - '';
  22.     }
  23. }
  24.  
  25. //使用string重置numB
  26. void resetNumB(string numBStr)
  27. {
  28.     memset(numB, , M * sizeof(int));
  29.  
  30.     //将字符串的每一位都转换成数字传入数组
  31.     for (int i = ; i < numBStr.length(); i++)
  32.     {
  33.         numB[i] = numBStr[numBStr.length() - i - ] - '';
  34.     }
  35. }
  36.  
  37. //将数组转换为字符串，用于输出
  38. string getNumString(int* num)
  39. {
  40.     string numString;
  41.     bool isBegin = false;
  42.     for (int i = M - ; i >= ; i--)
  43.     {
  44.         if (num[i] != )
  45.         {
  46.             isBegin = true;
  47.         }
  48.  
  49.         if (isBegin)
  50.         {
  51.             numString += num[i] + '';
  52.         }
  53.     }
  54.     return numString;
  55. }
  56.  
  57. //判断两个数字哪个大
  58. int compare(string numAStr, string numBStr)
  59. {
  60.     int i = ;
  61.     int la = ;
  62.     while (numAStr[i] == '') {
  63.         la++;
  64.         i++;
  65.     }
  66.     i = ;
  67.     int lb = ;
  68.     while (numBStr[i] == '') {
  69.         lb++;
  70.         i++;
  71.     }
  72.     string a(numAStr.substr(la, numAStr.length()));
  73.     string b(numBStr.substr(lb, numBStr.length()));
  74.     if (a.length() > b.length())
  75.     {
  76.         return ;
  77.     }
  78.     else if (a.length() < b.length())
  79.     {
  80.         return -;
  81.     }
  82.     else
  83.     {
  84.         for (int i = ; i < a.length(); i++)
  85.         {
  86.             if (a[i]>b[i])
  87.             {
  88.                 return ;
  89.             }
  90.  
  91.             if (a[i]<b[i])
  92.             {
  93.                 return -;
  94.             }
  95.         }
  96.         return ;
  97.     }
  98. }
  99.  
  100. //加法
  101. string sum(string numAStr, string numBStr)
  102. {
  103.     resetNumA(numAStr);
  104.     resetNumB(numBStr);
  105.  
  106.     for (int i = ; i < M; i++)
  107.     {
  108.         //结果保存在numA中
  109.         numA[i] += numB[i];
  110.  
  111.         //数字大于9则进位
  112.         if (numA[i]>)
  113.         {
  114.             numA[i] -= ;
  115.             numA[i + ]++;
  116.         }
  117.     }
  118.  
  119.     return getNumString(numA);
  120. }
  121.  
  122. //减法
  123. string sub(string numAStr, string numBStr)
  124. {
  125.     bool isNegative = false;
  126.  
  127.     //如果numA比numB小
  128.     //则结果为负数
  129.     //调换位置进行计算
  130.     if (compare(numAStr, numBStr) == -)
  131.     {
  132.         isNegative = true;
  133.         string temp = numAStr;
  134.         numAStr = numBStr;
  135.         numBStr = temp;
  136.     }
  137.     else if (compare(numAStr, numBStr) == )
  138.     {
  139.         return "";
  140.     }
  141.  
  142.     resetNumA(numAStr);
  143.     resetNumB(numBStr);
  144.  
  145.     for (int i = ; i < M; i++)
  146.     {
  147.         //减数小于被减数就借位
  148.         if (numA[i]<numB[i])
  149.         {
  150.             numA[i] = numA[i] +  - numB[i];
  151.             numA[i + ]--;
  152.         }
  153.         else
  154.         {
  155.             numA[i] -= numB[i];
  156.         }
  157.     }
  158.     if (isNegative)
  159.     {
  160.         return "-" + getNumString(numA);
  161.     }
  162.     else
  163.     {
  164.         return getNumString(numA);
  165.     }
  166.  
  167. }
  168.  
  169. //乘法
  170.  
  171. string mul(string numAStr, string numBStr)
  172. {
  173.     resetNumA(numAStr);
  174.     resetNumB(numBStr);
  175.  
  176.     vector<string> nums;
  177.     for (int i = ; i < numBStr.length(); i++)
  178.     {
  179.         //初始化一个临时数据来保存被乘数与乘数的某一位相乘的结果
  180.         int temp[M];
  181.         memset(temp, , M * sizeof(int));
  182.  
  183.         for (int j = i; j < numAStr.length() + i; j++)
  184.         {
  185.             temp[j] += numA[j - i] * numB[i] % ;
  186.  
  187.             temp[j + ] = numA[j - i] * numB[i] / ;
  188.  
  189.             //如果大于9，那么就做进位处理
  190.             if (temp[j]>)
  191.             {
  192.                 temp[j] -= ;
  193.                 temp[j + ]++;
  194.             }
  195.         }
  196.         nums.push_back(getNumString(temp));
  197.     }
  198.  
  199.     //每位相乘的结果再用加法加起来
  200.     string result = nums[];
  201.     for (int i = ; i < nums.size(); i++)
  202.     {
  203.         result = sum(result, nums[i]);
  204.     }
  205.  
  206.     return result;
  207. }
  208.  
  209. //除,结果精确到个位
  210. string div(string numAStr, string numBStr)
  211. {
  212.     resetNumA(numAStr);
  213.     resetNumB(numBStr);
  214.  
  215.     string result;
  216.     string left;
  217.  
  218.     if (compare(numAStr, numBStr) == -)
  219.     {
  220.         return "";
  221.     }
  222.  
  223.     //标记第一个不为0的位数的出现
  224.     bool flag = false;
  225.     for (int i = ; i < numAStr.length(); i++)
  226.     {
  227.         left += numAStr[i];
  228.  
  229.         //余数比除数大
  230.         if (compare(left, numBStr) == )
  231.         {
  232.             flag = true;
  233.  
  234.             int count = ;
  235.             string temp = numBStr;
  236.  
  237.             while (true)
  238.             {
  239.                 //每循环一次加上一个余数
  240.                 temp = sum(temp, numBStr);
  241.  
  242.                 //余数仍然大于除数，继续累加
  243.                 if (compare(left, temp) == )
  244.                 {
  245.                     count++;
  246.                 }
  247.                 //余数小于除数
  248.                 //可以计算结果
  249.                 else if (compare(left, temp) == -)
  250.                 {
  251.                     result += count + '';
  252.                     left = sub(left, sub(temp, numBStr));
  253.                     break;
  254.                 }
  255.                 //此时余数刚好是除数的倍数
  256.                 else if (compare(left, temp) == )
  257.                 {
  258.                     count++;
  259.                     result += count + '';
  260.                     left = "";
  261.                     break;
  262.                 }
  263.             }
  264.         }
  265.         //刚好除尽
  266.         else if (compare(left, numBStr) == )
  267.         {
  268.             flag = true;
  269.             result += "";
  270.             left = "";
  271.         }
  272.         //余数比除数小，跳到下一位
  273.         else if (flag)
  274.         {
  275.             result += "";
  276.         }
  277.  
  278.     }
  279.  
  280.     return result;
  281. }
  282. //取模
  283. string mod(string numAStr, string numBStr)
  284. {
  285.  
  286.     string result = "";
  287.  
  288.     if (compare(numAStr, numBStr) == -)
  289.     {
  290.         return numAStr;
  291.     }
  292.     else if (compare(numAStr, numBStr) == ) {
  293.         return result;
  294.     }
  295.     else {
  296.         string d = div(numAStr, numBStr);
  297.         string x = mul(numBStr, d);
  298.         result = sub(numAStr, x);
  299.         return result;
  300.     }
  301. }
  302.  
  303. //加密解密模幂算法
  304. string getMod(string m, string pow, string n)
  305. {
  306.     string temp;
  307.     while (compare(pow,"") == ) {
  308.         if(mod(pow,"")=="")
  309.             temp = temp + "";
  310.         else
  311.             temp = temp + "";
  312.         pow = div(pow,"");
  313.     }
  314.     temp = temp + "";
  315.     int length = temp.length();
  316.     string T[M];
  317.     string M = "";
  318.     T[] = mod(m, n);
  319.     for (int i = ; i < length; i++) {
  320.         T[i] = mod(mul(T[i-],T[i-]),n);
  321.     }
  322.     for (int i = ; i < length; i++) {
  323.         if (temp[i] == '') {
  324.             M = mul(M, T[i]);
  325.         }
  326.     }
  327.     string result = mod(M, n);
  328.     return result;
  329. }
  330.  
  331. //求2的n次方函数
  332. string mul_2(int i) {
  333.     string result = "";
  334.     for (int j = ; j < i; j++) {
  335.         result = mul(result, "");
  336.     }
  337.     if (i == )
  338.         return "";
  339.     else
  340.         return result;
  341. }
  342.  
  343. //求m的t次方函数
  344. string mul_m(string m,string t) {
  345.     string result = m;
  346.     string j;
  347.     for ( j = ""; compare(j, t) == -; j = sum(j, "")) {
  348.         result = mul(result, m);
  349.     }
  350.         return result;
  351. }
  1. #include<iostream>
  2. #include"operation.h"
  3. using namespace std;
  4.  
  5. int main() {
  6.     string char_number_p;
  7.     string char_number_q;
  8.  
  9.     string temp[][];
  10.     //p=17,q=11
  11.     //p=17,q=19
  12.     //p=41,q=43
  13.     //67,71
  14.     //797 809
  15.     //49993 49999
  16.     //116747 110221
  17.     //1000017077
  18.     //
  19.     char_number_p="";
  20.     char_number_q="";
  21.  
  22.     string n = mul(char_number_p, char_number_q);
  23.     string tmp1 = "";
  24.     string On = mul(sub(char_number_p, tmp1),sub(char_number_q, tmp1));
  25.  
  26.     string e = "";
  27.  
  28.     //拓展欧几里得算法
  29.     temp[][] = e;
  30.     temp[][] = "";
  31.     temp[][] = On;
  32.     temp[][] = "";
  33.     int i = ;
  34.     do {
  35.         temp[i][] = temp[i - ][];
  36.         temp[i][] = "";
  37.         temp[i][] = temp[i - ][];
  38.         temp[i][] = "";
  39.         if (compare(temp[i][], temp[i][]) == ) {
  40.             temp[i][] = mod(temp[i][], temp[i][]);
  41.         }
  42.         else {
  43.             temp[i][] = mod(temp[i][], temp[i][]);
  44.         }
  45.         i++;
  46.     } while (compare(temp[i - ][], "") == );
  47.     int value = i - ;
  48.     temp[value][] = "";
  49.     value--;
  50.     while (value >= ) {
  51.         if (temp[value + ][] != "")
  52.             temp[value][] = div(sub(mul(temp[value][], temp[value + ][]), ""), temp[value][]);
  53.         else if (temp[value + ][] != "")
  54.             temp[value][] = div(sum(mul(temp[value][], temp[value + ][]), ""), temp[value][]);
  55.         value--;
  56.     }
  57.     string d = temp[][];
  58.  
  59.     cout << "e:" << e << endl;
  60.     cout << "p*q:" << n << endl;
  61.     cout << "O(n):" << On << endl;
  62.     cout << "d:" << d << endl;
  63.     cout << "密钥{ " << e << " , " << n << " }" << endl;
  64.     cout << "公钥{ " << d << " , " << char_number_p <<" , "<< char_number_q << " }" << endl;
  65.  
  66.     string miwen;
  67.     cout << "请输入密文(暂小于10的29次方)" << endl;
  68.     cin >> miwen;
  69.     cout << "密文:" << miwen << endl;
  70.     string C1 = getMod(miwen, e, n);
  71.     cout << "加密后的明文:" << C1 << endl;
  72.     string M1 = getMod(C1, d, n);
  73.     cout << "解密后的密文:" << M1 << endl;
  74.  
  75.     cout << "请输入密文(暂小于10的29次方)" << endl;
  76.     cin >> miwen;
  77.     string C2 = getMod(miwen, e, n);
  78.     cout << "加密后的明文:" << C2 << endl;
  79.     string M2 = getMod(C2, d, n);
  80.     cout << "解密后的密文:" << M2 << endl;
  81.  
  82.     cout << "请输入密文(暂小于10的29次方)" << endl;
  83.     cin >> miwen;
  84.     string C3 = getMod(miwen, e, n);
  85.     cout << "加密后的明文:" << C3 << endl;
  86.     string M3 = getMod(C3, d, n);
  87.     cout << "解密后的密文:" << M3 << endl;
  88.  
  89.     system("pause");
  90.     return ;
  91. }

以上为测试实现的代码。

思路：先实现string类型的加减乘除的重写，以及用到的其他的操作函数，比较，取模，加解密函数，以及其他的m的n次方的操作。

然后在主函数里面嵌入欧几里得算法，调用求得d，之后就是简单的调用加解密函数

pq的值也是测试得到的

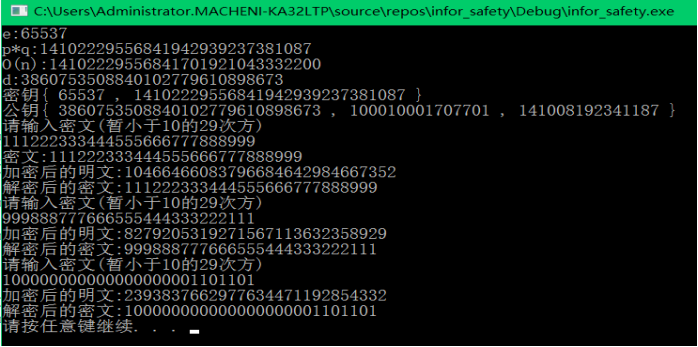
这是运行截图：

  1. //拓展欧几里得算法
  2.     temp[0][0] = e;
  3.     temp[0][1] = "";
  4.     temp[0][2] = On;
  5.     temp[0][3] = "";
  6.     int i = 1;
  7.     do {
  8.         temp[i][0] = temp[i - 1][0];
  9.         temp[i][1] = "";
  10.         temp[i][2] = temp[i - 1][2];
  11.         temp[i][3] = "";
  12.         if (compare(temp[i][0], temp[i][2]) == 1) {
  13.             temp[i][0] = mod(temp[i][0], temp[i][2]);
  14.         }
  15.         else {
  16.             temp[i][2] = mod(temp[i][2], temp[i][0]);
  17.         }
  18.         i++;
  19.     } while (compare(temp[i - 1][0], "1") == 1);
  20.     int value = i - 1;
  21.     temp[value][1] = "1";
  22.     value--;
  23.     while (value >= 0) {
  24.         if (temp[value + 1][1] != "")
  25.             temp[value][3] = div(sub(mul(temp[value][0], temp[value + 1][1]), "1"), temp[value][2]);
  26.         else if (temp[value + 1][3] != "")
  27.             temp[value][1] = div(sum(mul(temp[value][2], temp[value + 1][3]), "1"), temp[value][0]);
  28.         value--;
  29.     }
  30.     string d = temp[0][1];
    这部分拓展的欧几里得算法也可以单独使用，这里是用空间换取的时间效率。

RSA算法的C++string实现(模幂算法和欧几里得算法的使用)后附思路的更多相关文章

  1. RSA简介(二)——模幂算法

    RSA最终加密.解密都要用到模乘的幂运算,简称模幂运算. 回忆一下RSA,从明文A到B B=Ae1%N 对B解密,就是 A=Be2%N 其中,一般来说,加密公钥中的e1一般会比较小,取65537居多, ...

  2. Java数据结构与算法之---求两个数的最大公约数（欧几里得算法）

    一个简单的小算法来获取两个数的最大公约数, public class Test { public static void main(String[] args) { long result = gcd ...

  3. Modular_exponentiation模幂运算

    https://en.wikipedia.org/wiki/Modular_exponentiation 蒙哥马利(Montgomery)幂模运算是快速计算a^b%k的一种算法,是RSA加密算法的核心 ...

  4. [技术栈]C#利用Luhn算法(模10算法)对IMEI校验

    1.Luhn算法(模10算法) 通过查看ISO/IEC 7812-1:2017文件可以看到对于luhn算法的解释,如下图: 算法主要分为三步: 第一步:从右边第一位(最低位)开始隔位乘2: 第二步:把 ...

  5. LeetCode算法题-Reverse String II（Java实现）

    这是悦乐书的第256次更新,第269篇原创 01 看题和准备 今天介绍的是LeetCode算法题中Easy级别的第123题(顺位题号是541).给定一个字符串和一个整数k,你需要反转从字符串开头算起的 ...

  6. LeetCode算法题-Reverse String（Java实现）

    这是悦乐书的第205次更新,第217篇原创 01 看题和准备 今天介绍的是LeetCode算法题中Easy级别的第73题(顺位题号是344).编写一个以字符串作为输入并返回字符串的函数.例如: 输入: ...

  7. RSA加密解密，String转PublicKey、PrivateKey；附Base64.JAR

    网络请求的数据需要加密,服务器给的他们那一套在Android一直报错,自己写了一个: package com.cc.common.util; import javax.crypto.Cipher; i ...

  8. 银行卡号码校验算法（Luhn算法，又叫模10算法）

    有时候在网上办理一些业务时有些需要填写银行卡号码,当胡乱填写时会立即报错,但是并没有发现向后端发送请求,那么这个效果是怎么实现的呢. 对于银行卡号有一个校验算法,叫做Luhn算法. 一.银行卡号码的校 ...

  9. 数模常用算法系列Matlab实现-----线性规划

    线性规划的 Matlab 标准形式 线性规划的目标函数可以是求最大值,也可以是求最小值,约束条件的不等号可以是小于号也可以是大于号.为了避免这种形式多样性带来的不便,Matlab 中规定线性 规划的标 ...

随机推荐

  1. 分布式session解决——Spring-data-redis

    1.如果没有集成shiro来管理session,可以直接使用spring-session 2.若集成了shiro,需要Spring-data-redis (或 shiro-redis) 3.nginx ...

  2. 初始Mkaefile

    初识MakefIle 在学习Linux过程中,我越发的觉得Linux系统给了使用者更大的自由,同时也就增加了学习的成本.在gcc下去调试代码,没有了熟悉的VS,没有的人性话的错误提示(当然Makefi ...

  3. leetcode算法题整理

    一.线性表,如数组,单链表,双向链表 线性表.数组 U1.有序数组去重,返回新数组长度 A = [1,1,2] -> [1,2] 返回2   分析:其实一般数组的问题都可以用两个指针解决,一个指 ...

  4. H5实现全屏与F11全屏

    最近做项目用到全屏,现总结一下全屏: 1.局部全屏:H5全屏和F11有区别,在这种情况下判断全屏只需要通过H5全屏属性,无论全屏后有无滚动条都可判断. /** * [isFullscreen 判断浏览 ...

  5. MySQL数据库表损坏后的修复方法

    步骤:1.sql语句:check table tabTest; 如果出现的结果说Status是OK,则不用修复,如果有Error2.Linux执行: myisamchk -r -q /var/lib/ ...

  6. SourceTree安装跳过登录

    安装 SourceTree 时,需要使用atlassian授权,因为各种原因无法完成授权,现提供跳过 atlassian账号 授权方法. 安装之后,转到用户本地文件夹下的 SourceTree 目录, ...

  7. ASP.NET Core 从 gitlab-ci 环境变量读取配置

    最近在加强持续集成,遇到一个场景需要通过 gitlab-ci 环境变量(Settings -> Settings -> CI/CD -> Variables )在持续集成时向 ASP ...

  8. Lambda查询

    使用EF查询数据库,之前使用Linq表达式,现在改成另一个种方法查询:Lambda表达式 TestEntities db=new TestEntities(); ).FirstOrDefault(); ...

  9. [04-05]box框模型(Box Model)定义了元素框处理元素内容、内边距、边框和外边距的方式

    实际占有的宽 = width + 2padding(内边距) + 2border(边框) + 2margin(外边距) 实际占有的高 = height + 2padding + 2border + 2 ...

  10. 输入URL地址到页面加载完成 过程

    在浏览器的地址栏中输入URL地址"http://www.gacl.cn:8080/JavaWebDemo1/1.jsp"去访问服务器上的1.jsp这个web资源的过程 1.浏览器根 ...