Tarjan求割点(割顶) 割边(桥)

割点的定义:

　　感性理解，所谓割点就是在无向连通图中去掉这个点和所有和这个点有关的边之后，原先连通的块就会相互分离变成至少两个分离的连通块的点。

　　　举个例子： 图中的4号点就是割点，因为去掉4号点和有关边之后连通块{1,2,3} {5} {6}就相互分离了。

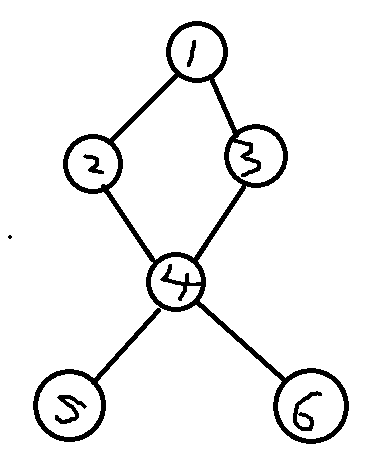
图片来自：一篇写的较好的blog：https://www.cnblogs.com/jason2003/p/7603886.html

　　

Tarjan算法求割点：

　　有好多个Tarjan算法，不要傻傻分不清~~

　　其实和有向图求强连通分量的Tarjan算法差不多啦，也用到了dfn和low。

　　因为是无向连通图，所以横向边是没有意义的，(有反向边的存在)。

　　dfn[u]：u在搜索树中被遍历到的次序号(时间戳)。

　　low[u]：u或u的子树中的结点经过最多一条后向边能追溯到的最早的树中结点的次序号(dfn),有点懵，先不管他，感性理解就是通过边到达的点的最小时间戳。

割点判断条件：

　　①：若u为树的树根，那么只要u有两个及以上的子节点，那么只要u点消失，子节点所在的连通块就会分离了。

如果只有一个子节点，那么u消失之后还剩下那个子节点的连通块，仍是一个并不是多个。

　　②：若u不为树根，v不为u的父结点，当dfn[u]<=low[v]时，u就为割点，由该式子的含义可得，v以及v的子树最多只能到达u结点，

不能到达u的祖先，此时删掉u，那么(v及v的子树)和(u的祖先)就会相互分离了，自然u就是割点。

　　求割点时若(u,v)为后向边，v不为u的父结点，low[u]=min{low[u],dfn[v]}，里面一定要写dfn[v]，不能写low[v]。

原因详见：https://www.luogu.org/blog/ztyluogucpp/solution-p3388

割点模板：

　　L3388 【模板】割点（割顶）：https://www.luogu.org/problemnew/show/P3388

#include<bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
#define ll long long
#define maxn 100009
inline ll read()
{
    ll x=,f=;char ch=getchar();
    while(ch<''||ch>''){if(ch=='-')    f=-;ch=getchar();}
    while(ch>=''&&ch<=''){x=(x<<)+(x<<)+(ll)(ch-'');ch=getchar();}
    return x*f;
}
int head[maxn],dfn[maxn],low[maxn],point[maxn];
int n,m,k,ans,cnt,id,tot,root;
struct edge
{
    int to,nxt;
}p[maxn<<];

void add(int x,int y)
{
    ++cnt,p[cnt].to=y,p[cnt].nxt=head[x],head[x]=cnt;
}

void Tarjan(int u,int fa)
{
    dfn[u]=low[u]=++id;
    int child=;
    for(int i=head[u];i;i=p[i].nxt)
    {
        int v=p[i].to;
        if(!dfn[v])
        {
            Tarjan(v,u);
            low[u]=min(low[u],low[v]);
            if(u!=root&&low[v]>=dfn[u])
                point[u]=;
            if(u==root&&++child>=)
                point[u]=;
        }
        else
            low[u]=min(low[u],dfn[v]);
    }

}
int main()
{
//    freopen(".in","r",stdin);
//    freopen(".out","w",stdout);
    n=read(),m=read();
    for(int i=;i<=m;i++)
    {
        int x=read(),y=read();
        add(x,y),add(y,x);
    }
    for(int i=;i<=n;i++)
        if(!dfn[i])
            root=i,Tarjan(i,i);
    for(int i=;i<=n;i++)
        if(point[i])
            tot++;
    printf("%d\n",tot);
    for(int i=;i<=n;i++)
        if(point[i])
            printf("%d ",i);
    fclose(stdin);
    fclose(stdout);
    return ;
}

割边的定义：

　　和割点的定义类似，只不过是把去掉点以及与点有关的边改成了去掉这条边看是否连通就行啦。

Tarjan算法求割边：

　　和求割点只有一点点小区别...

　　　因为有可能存在重边的问题，所以要将一条无向边拆为两条编号一样的有向边，用邻接表进行储存，在判断(u,v)是否为后向边的时候要注意判断是树枝边的反向边还是新的一条边。

割边判断条件:

　　dfn[u]<low[v],不可以取等号，因为取等号意味着v及v的子树能够到达结点u，那么(u,v)这条边自然就不是割边了。

　　

割边模板：

　　L1656 炸铁路：https://www.luogu.org/problemnew/show/P1656

　　裸的割边模板，虽然不需要判断重边但是还是加上比较好，再用优先队列维护一下答案就可以了。

　　判断是否是树枝边的反向边的时候只需要判断vis[i^1]是否等于1就行了，因为是这样判断的，所以在建边的时候cnt必须从1开始，因为0^1=0,并不会得到1这条反向边。

#include<bits/stdc++.h>
using namespace std;
#define re register int
#define ll long long
#define INF 0x3f3f3f3f
#define maxn 159
#define maxm 5009
inline ll read()
{
    ll x=,f=;char ch=getchar();
    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
    while(ch>=''&&ch<=''){x=(x<<)+(x<<)+(ll)(ch-'');ch=getchar();}
    return x*f;
}
priority_queue<pair<int,int> >q;
int head[maxn],dfn[maxn],low[maxn];
bool vis[maxm<<];
int n,m,k,ans,tot,id,cnt=;
struct edge
{
    int to,nxt;
}p[maxm<<];

void add(int x,int y)
{
    p[++cnt]={y,head[x]},head[x]=cnt;
}

void Tarjan(int u)
{
    dfn[u]=low[u]=++id;
    for(int i=head[u];i;i=p[i].nxt)
    {
        if(vis[i^])
            continue;
        int v=p[i].to;
        vis[i]=;
        if(!dfn[v])
        {
            Tarjan(v);
            low[u]=min(low[u],low[v]);
            if(dfn[u]<low[v])
                q.push(make_pair(-min(u,v),-max(u,v)));
        }
        else
            low[u]=min(low[u],dfn[v]);
    }
}
int main()
{
//    freopen(".in","r",stdin);
//    freopen(".out","w",stdout);
    n=read(),m=read();
    for(int i=;i<=m;i++)
    {
        int x=read(),y=read();
        add(x,y),add(y,x);
    }
    for(int i=;i<=n;i++)
        if(!dfn[i])
            Tarjan(i);
    while(q.size())
    {
        printf("%d %d\n",-q.top().first,-q.top().second);
        q.pop();
    }
    fclose(stdin);
    fclose(stdout);
    return ;
}