OO_BLOG1_简单表达式求导问题总结

作业1-1 包含简单幂函数的多项式导函数的求解

I. 基于度量的程序结构分析

1）程序结构与基本度量统计图

2）分析

​ 本人的第一次作业的程序实现逻辑十分简单，但是OOP的色彩并不强烈，程序耦合度过高。

• Homewk类： judge()：输入合法性判断； process()，getTerm()：输入处理； output()：输出处理； main()：主函数；
• Term类： division()：将Term识别为二元数组； derivation()：实现Term的求导；

II. 程序BUG分析

1）自身错误

​ 本次测试，强测测试中有三个数据测试未通过，报错信息均为“Your answer has format error”。错误分析如下：

STDOUT	ANSWER
**-8642051***x-51x998x-40x-57x^-91	-8642051
-85070591730234615875067023894796828672x-9223372036854775810*x-82 +85070591730234615911960512042215931910***x9223372036854775810***x-100x-70*x-29*x^-30	-85070591730234615875067023894796828672x^-9223372036854775810+ 85070591730234615911960512042215931910x^9223372036854775810

*第三个数据点过长，既为同质错误，故暂不列出

​ 观察错误输出与标准输出，可以发现，程序输出时，在正确结果之后冗余了一串字符。经过分析，发现冗余的字符串来自系数为0的项，于是去检测output()函数，最终找出bug：输出判断逻辑错误——系数是否为0的判断与其他输出处理的逻辑应为包含关系，原程序错写为并列关系。

2）他人错误

• 过长数据爆栈

  e.g. +x+x+x+x...+x {500, }

  原因：输入匹配时使用一个大正则表达式暴力匹配；未用BigInteger等进行运算。

  解决方法：运用拆分匹配或者字符自动机；使用大整数的处理机制。

• 部分非法输入无法识别

  e.g. \f, \v, 空输入 （文件输入）

  原因：未对这些特殊情况进行处理。

  解决方法：输入时进行空输入和非法字符的检验；利用try-catch提高程序的鲁棒性。

III. 程序测试策略

1）白盒测试

• 第一次作业的代码量较小，进行白盒测试的代价相对较小，且效果更好。
• 白盒测试可以增强阅读理解代码的能力。
• 我的阅读顺序是先观察程序的Diagram，然后从main函数开始，由数据输入到输入判断，再到输入处理，最后到数据输出，一步步探索同学们的代码。

2）黑盒测试

• 相信大多数同学在自己编写程序时，或在与同学朋友们交谈的过程中，对可能出错的数据点有了一些初步的把握，在互测阶段，可以利用这些头脑风暴的结果进行测试，这种测试往往具有较强的针对性；
• 周围优秀的同学们应用各种工具编写了对拍器与评测机，在评测时应用这些可以大大节省掉重复的机械试错带来的时间消耗。

IV. 关于程序优化的思考

1）结构优化

• 将现有Term类、Homewk类拆分成Term类、Handler类和Main类：Term类包含系数、幂以及求导的方法，Handler类包含输入判断和字符串处理的方法；Main类里包含有main函数，负责将输入、处理与输出串联起来。

2）输出优化

• 当输出的结果中的项有多个，且有正有负，则正项应先输出。

作业1-2 包含简单幂函数和简单正余弦函数的导函数的求解（不支持嵌套规则）

I. 基于度量的程序结构分析

1）程序结构与基本度量统计图

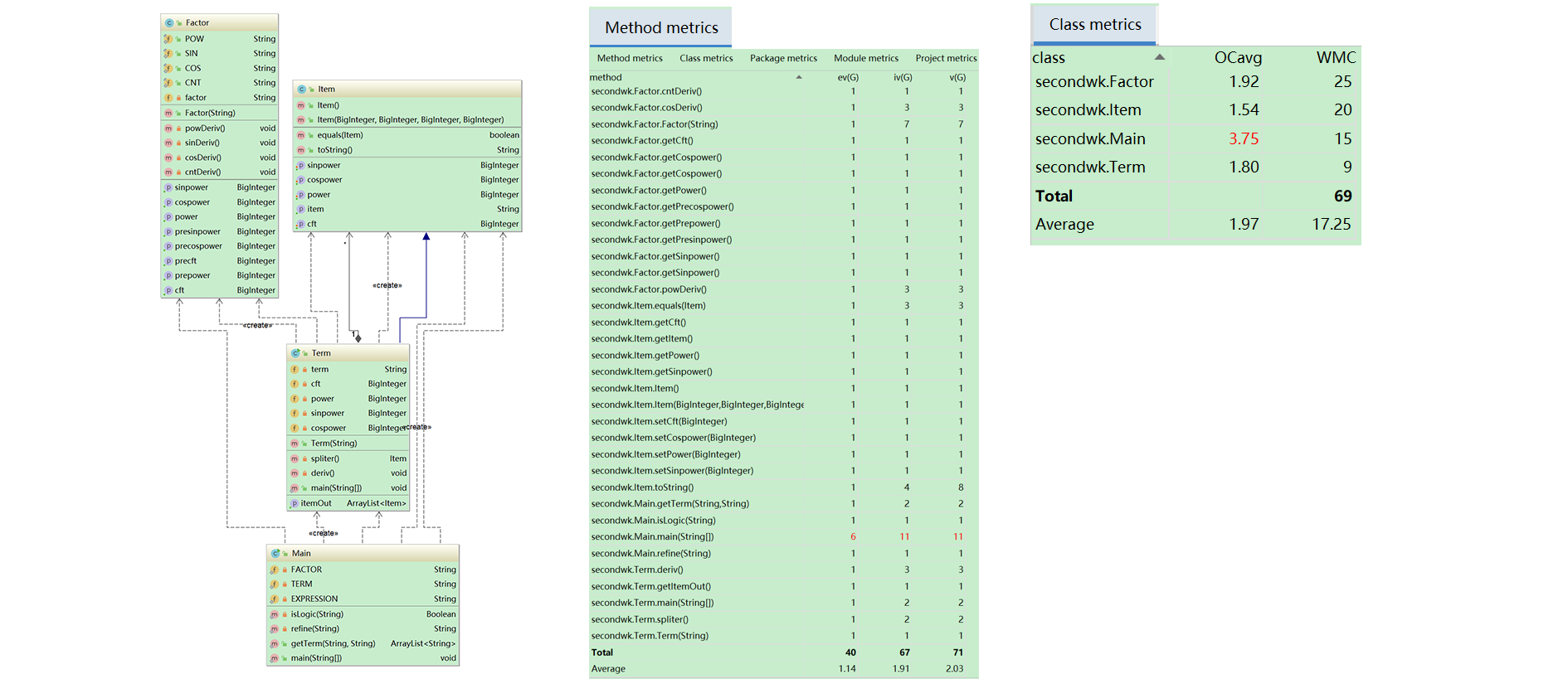
2）分析

​ 本次作业，我的基本思路是将每一项转化为 \(a·x^b·sin^c(x)·cos^d(x)\) 的标准格式，按照求导公式计算出结果。本题所用求导公式如下，

\(df/dx = a·[ b·x^{b-1}·sin^c(x)·cos^d(x)+c·x^b·sin^{c-1}(x)·cos^{d+1}(x)-d·x^b·sin^{c+1}(x)·cos^{d-1}(x)]\)

• Item类定义了“标准项”，即符合通项公式 \(a·x^b·sin^c(x)·cos^d(x)\) 的一个项，可以实现项的求导；
• Term类定义了”普通项“（它是Item类的子类），每一个项由一个或多个因子按照乘法规则构成，可以实现将Term类型的对象转化为Item类的对象的方法；
• Factor类定义了”因子“，可以实现因子的求导；
• Main类里包含有main函数，负责将输入、处理与输出串联起来。

II. 程序BUG分析

1）自身错误

​ 本次测试，互测有三个测试点未通过，报错信息均为”Your answer has format error“。错误分析如下，

STDIN	STDOUT	ANSWER
sin( x )	WRONG FORMAT!	cos(x)
(space)1	WRONG FORMAT!	0
x*sin(x )	WRONG FORMAT!	sin(x)+x*cos(x)

​ 观察程序输入、输出与正确答案可知，输入判断格式有问题。经过输入判断正则表达式的简单修改，即得到正确答案。

2）他人错误

• 部分非法输入字符无法识别

  e.g. (space)+++1, \f, \v

  原因：未对这些特殊情况进行处理。

  解决方法：输入时进行非法字符的检验；利用try-catch提高程序的鲁棒性；正确理解实验指导书所规定的正确规范。

• 求导计算错误

  e.g. 优化输出时将幂为0的整个项全部删去，使结果出错。

  原因：优化中考虑疏忽，导致最终结果出错。

  解决方法：谨慎优化，大力测试。

III. 程序测试策略

1）白盒测试

• 本次作业代码量略有提升，由于出现三角函数合并的优化，容易出现错误，检查代码时可以有所侧重。

2）黑盒测试

• 由于本次作业程序输出可能较为复杂，肉眼很难判断正误，自动化评测显得必不可少。在此鸣谢伯格提供的评测代码，大大降低了测试的复杂度。
• 自动化测试带来方便，但是也有弊端，即评测得到的错误多为同质，但由于输入输出往往较长，肉眼依旧难辨。为解决这一问题，我采取了观察+人工修改重测的方法，效率较低但是最终结果可靠。

IV. 关于程序优化的思考

1）结构优化

• 将数据输入以及数据判断与处理从Main类里剥离出来，形成一个新的InputHandler类。

2）输出优化

• 仔细阅读了何岱岚同学的优化思路后，其”化成三元组+贪心&随机合并“的策略虽未能完全领会，但依然受益匪浅。

作业1-3 包含简单幂函数和简单正余弦函数的导函数的求解（支持嵌套规则）

I. 基于度量的程序结构分析

1）程序结构与基本度量统计图

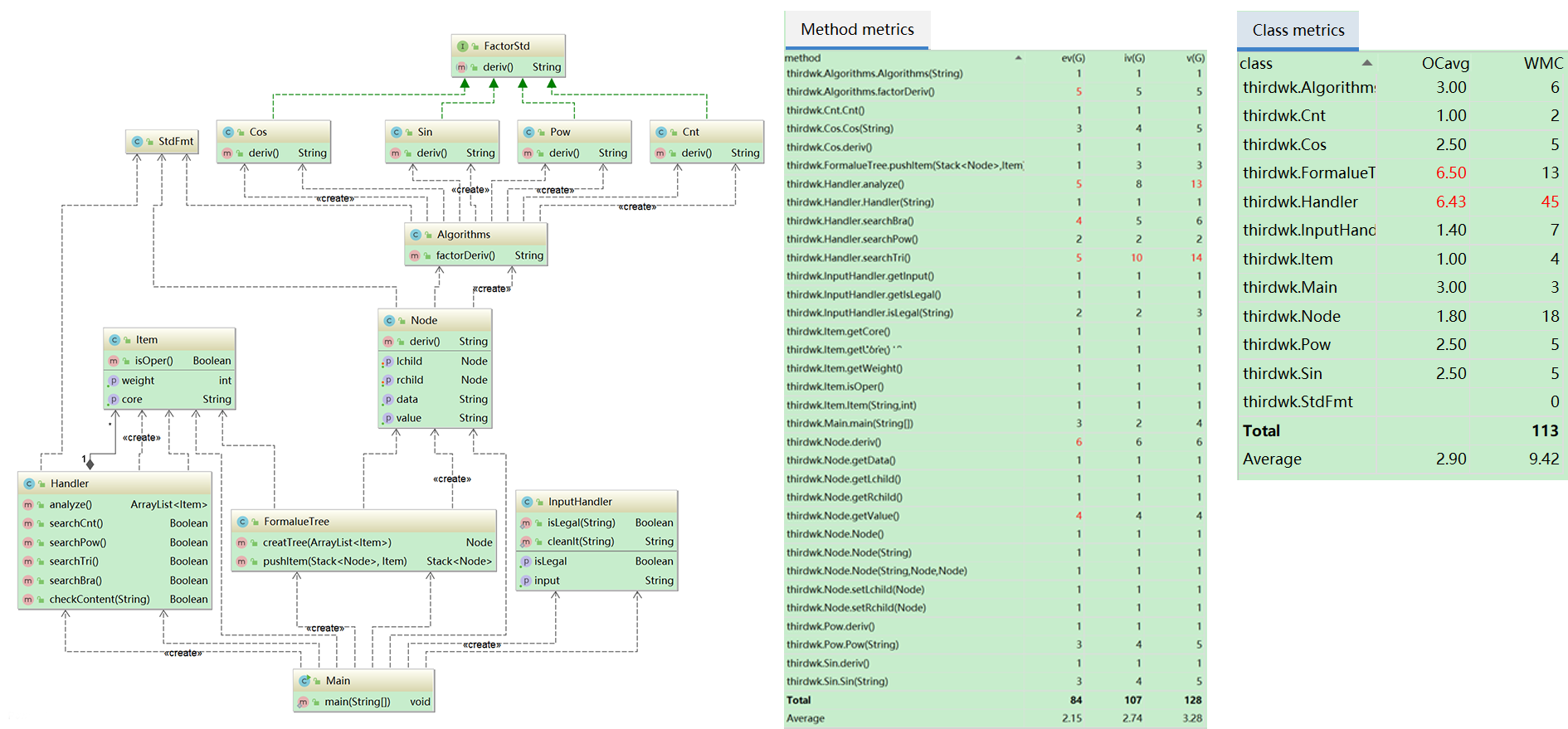
2）分析

本次作业是OO课程第一单元的重头戏。下面对本次程序进行分析。

• Main类：包含有main函数，负责将输入、处理与输出串联起来；

• InputHandler类：可实现输入合法性检测，输入处理；

• Hander类：分析输入的表达式字符串，将分析结果储存到动态数组中，具体分析算法详见下文；

• Item类：定义了上述动态数组元素的类型，包括权重(weight)和内容(core)；

• FormalueTree类：根据Handler形成的动态数组，用双栈法生成表达式树；

• Node类：定义了树节点以及树节点的求导(derivate)以及取字符串(getValue)的方法；

• FactorStd接口 + Cnt类&Cos类&Sin类&Pow类：分别实现常数因子、三角函数型因子、幂函数因子的求导；

• Algorithms类：统一上述四种因子求导的实现；

• StdFmt类：定义了程序所需的正则表达式；

  下面是Handler类中分析表达式字符串的算法。

• 

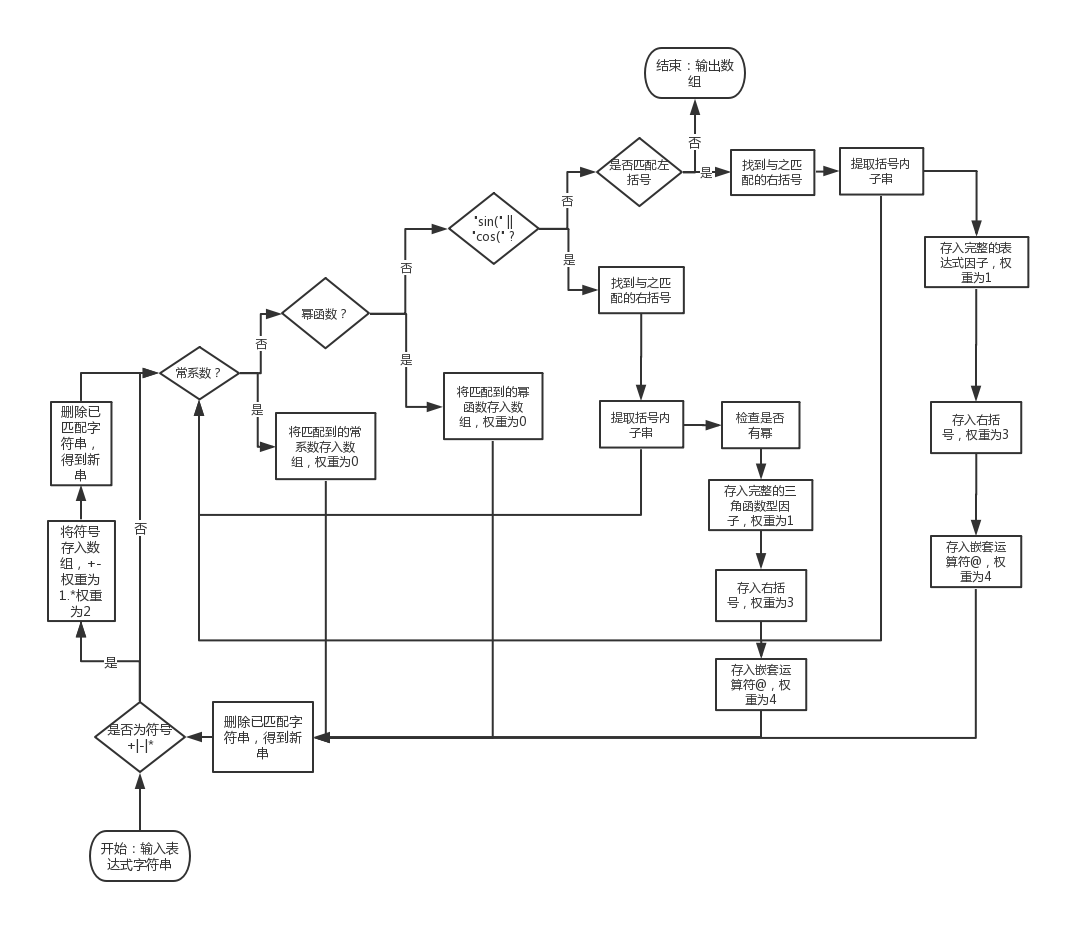
  下面是程序main函数的代码，展示了程序的基本逻辑。

  public static void main(String[] args) {
          try {
              /** 输入判断与输入处理 */
              Scanner in = new Scanner(System.in);
              if (!in.hasNextLine()) {
                  throw new RuntimeException("EMPTY INPUT!");
              }
              FormalueTree formalueTree = new FormalueTree();
              String input = in.nextLine();
              InputHandler inputHandler = new InputHandler(input);
              if (!inputHandler.getIsLegal()) {
                  throw new RuntimeException("ILLEGAL INPUT!");
              }
              /** 字符串分析 */
              Handler handler = new Handler(inputHandler.getInput());
              ArrayList<Item> items = handler.analyze();
              /** 构建表达式树 */
              Node root = formalueTree.creatTree(items);
              /** 求导并输出结果 */
              System.out.println(root.deriv());
          } catch (RuntimeException e) {
              System.out.print("WRONG FORMAT!\n" + e.getMessage());
          }
      }
  

II. 程序BUG分析

1）自身错误

​ 本次测试，强测点有4个未通过，互测点有13个未通过，数目令人触目惊心，但是仔细分析以后，发现错误点有二，现分析如下，

STDIN	STDOUT	ANSWER
(((((((((((((((((((( + 2*x ))))))))))))))))))))	WRONG FORMAT!	2
sin(((x-x)*x^+1+++1))	WRONG FORMAT!	0
1*+1	WRONG FORMAT!	0
sin(x)*-2	WRONG FORMAT!	0

*表中测试点已覆盖所有错误，其余测试点暂不列出

• 前两个测试点暴露的错误为，拆括号的嵌套时括号检测错误：

  public Boolean searchBra() {
          Matcher m = StdFmt.BRACEL.matcher(poly);
          if (m.lookingAt()) {
              int flag = 1;
              // for (int i = 2; i < poly.length(); i++) {   <——— 错误所在 ！！
              for (int i = 1; i < poly.length(); i++) { 	// <——— 正确结果 ！！
                  if (poly.charAt(i) == '(') {
                      flag += 1;
                  } else if (poly.charAt(i) == ')') {
                      flag -= 1;
                  }
                  if (flag == 0) {
                      /**
                      实现子串提取，递归拆除嵌套
                      */
                      return true;
                  }
              }
          }
          return false;
      }
  

• 后两个测试点暴露的错误为进行”树上求导“时，递归终止条件疏漏了带符号整数这一种因子：

  public String deriv() {
          switch (this.data) {
              case "+":
              case "-":
                  return "(" + this.rchild.deriv() + ")" +
                          this.data + "(" + this.lchild.deriv() + ")";
              case "*":
                  return "(" + this.rchild.deriv() + ")*(" +
                          this.lchild.getValue() + ")+(" +
                          this.rchild.getValue() + ")*(" +
                          this.lchild.deriv() + ")";
              case "@":
                  return "(" + this.rchild.deriv() + ")*(" +
                          this.lchild.deriv() + ")";
              default:
                  Matcher m = StdFmt.FACTOR.matcher(this.data);
                  /**
                  终止条件的格式判断应为
                  public static final Pattern FACTOR =
             		Pattern.compile("((x(\\^[+-]?\\d+)?)|(sin)|(cos)|([+-]?\\d+))");
             		错写为
             		public static final Pattern FACTOR =
             		Pattern.compile("((x(\\^[+-]?\\d+)?)|(sin)|(cos)|(\\d+))");
             		故当乘号（*）后含带符号整数，会抛出异常”Derivte Fault!“，程序出错。
                  */
                  if (m.lookingAt()) {
                      Algorithms algorithms = new Algorithms(this.data);
                      return algorithms.factorDeriv();
                  } else {
                      throw new RuntimeException("Derivte Fault!!");
                  }
          }
      }
  

2）他人错误

• 某些错误输入无法识别

  e.g. sin( - 1)

• 输出中某些因子缺少括号导致结果出错

  e.g. 负整数无括号，导致运算顺序出错

• 多重嵌套爆栈

  e.g. ((((((((((((((((((((((((((x))))))))))))))))))))))))))

  原因：递归层次太深等。

  解决方法：输入判断要慎重，选取恰当算法；递归优化时要注意等。

• 正确输入错判

  e.g. sin(x)^+12, x^-2

III. 程序测试策略

• 本次作业程序结构较为复杂，反而可以通过分析，想出大量的不同方面的测试用例，在实际应用中，也颇有效用，如对表达式因子识别不够全面（尤其是首项为+1或-1的特殊情况），多层嵌套，带幂的三角函数型因子的处理和计算等等；
• 本次程序测试的输出较长，适宜用评测程序进行数据比照；
• 用评测程序评测时，出现大量的同质错误，我采取“修补+测试”的方法，提高最终测试结果的准确性。

IV. 关于程序优化的思考

1）结构优化

• 反思：本次程序基本上是面向过程的编码，大多数类的效果基本等同于一个函数，类之间的耦合度非常高。
• 首先是输入判断的优化，本次我的输入判断其实并不是在一开始就判断好的，而是在之后计算和处理的过程中，通过不断地抛出异常来降低程序错误的概率，程序鲁棒性十分之低。拟采用课程组提供的字符自动机的方法进行优化改造
• 后面的优化，没有想出来较好的方案，希望能够在学习助教的总结PPT以及优秀同学们的代码后，有所启发。

2）输出优化

• 改造Node类：在lchild(Node)与rchild(Node)之外增加father(Node)，使父子节点双向链接。

• 输出处理：将原输出构建成表达式树，遍历节点，如果节点为运算符，则查询它的子节点(getValue)，根据一定规则“清理树枝”，最后getValue()得到清爽输出。规则示例如下，

  

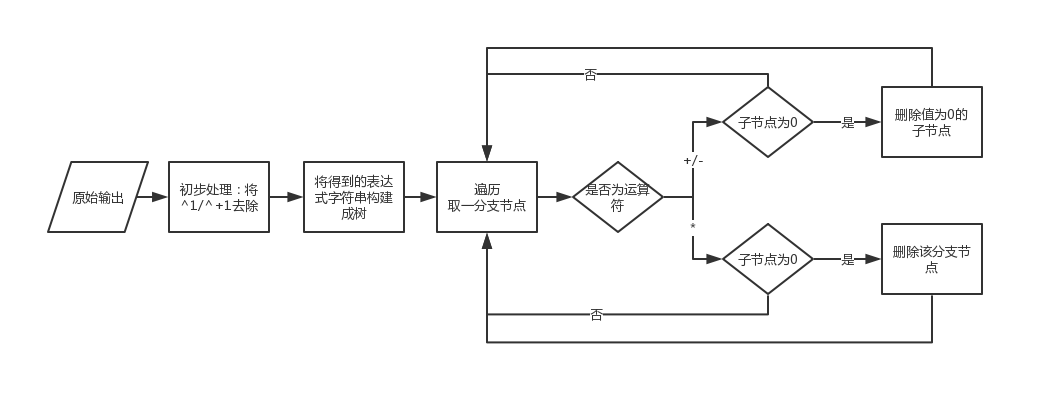
作业1-4 面向对象课程第一单元学习感想

I. 对自己的程序要狠一点， 对自己的程序要狠一点， 对自己的程序要狠一点；

II. 编写代码前的构思十分重要，但是如果真的毫无头绪，不妨动手小试，灵感也许会不期而至；

III. 面向对象的思维方式不是一蹴而就的，课堂之外需要多读代码，多做练习；

IV. 要提高自己新旧知识的融会贯通能力，复习与预习双轨并行；

V. 要调整好自己的心态，不要过于畏惧，更不要懈怠！

最后，衷心感谢为这门课程辛苦付出的老师和助教。