【同余方程组】POJ1006 生理周期

同余方程组：

　　先来看一道题目：有物不知其数，三三数之剩二；五五数之剩三；七七数之剩二。问物几何?  然后我们可以做如下变换，设x为所求的数。

　　　x%3=2              x ≡ a₁(%m₁)  ①
　　　x%5=3  ===>  x ≡ a₂(%m₂)  ②
　　　x%7=2              x ≡ a₃(%m₃)

　　根据前面两式可以得到

　　　　x = a₁+m₁y₁     (1)
　　　x = a₂+m₂y₂

　　两式相减得到  m₁y₁ - m₂y₂ = a₂ - a₁  这是一个线性不定方程,可解出y₁  ---> linearEquation(m₁,-m₂,a₂-a₁)   带回(1),得特解x₀ = a₁+m₁*y₁ --> 得到通解表达式 x =x₀ + k*lcm(m₁,m₂) 得一个新方程 x = x₀ (mod lcm(m₁,m₂))

　　代码：

/**
 *
 * @param a 余数组成的数组
 * @param m 模组成的数组
 * @return
 * @throws Exception
 */
public static long linearEquationGroup(Long[] a, Long[] m) throws Exception {
  int len = a.length;
  if (len == 0 && a[0] == 0)
    return m[0];

  for (int i = 1; i < len; i++) {
    // 这里往前看是两个方程
    long a2_a1 = a[i] - a[i - 1];
    long d = linearEquation(m[i - 1], -m[i], a2_a1);
    // 现在的x是y1,用y1求得一个特解
    long x0 = a[i - 1] + m[i - 1] * x;
    long lcm = m[i - 1] * m[i] / d;
    a[i] = (x0 % lcm + lcm) % lcm;// x0变成正数
    m[i] = lcm;
  }
  // 合并完之后,只有一个方程 : x = a[len-1] (% m[len-1])
  //long d = linearEquation(1, m[len-1], a[len-1]);
  return a[len - 1] % m[len - 1];
}

题目：POJ1006 生理周期

　　

　　

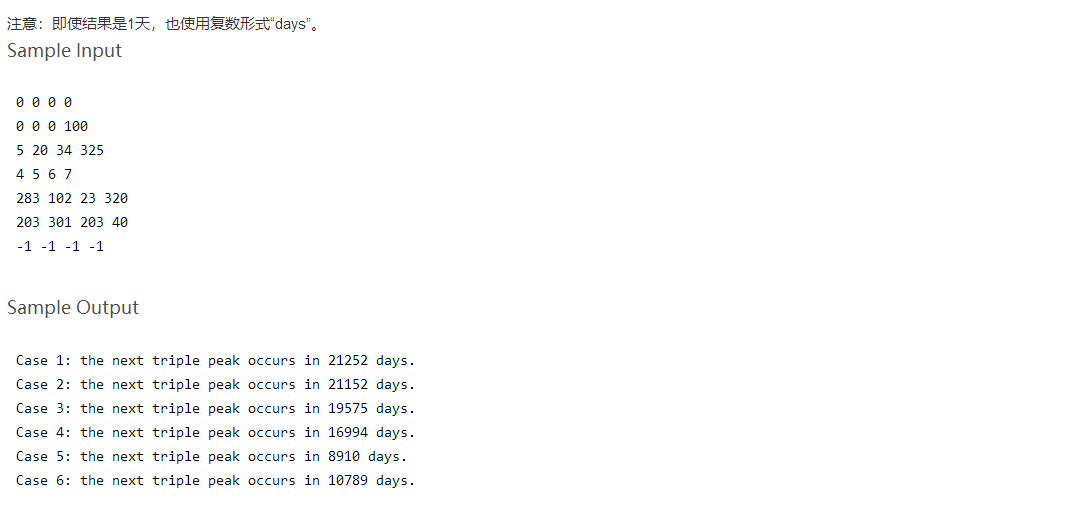
　　代码：

 import java.util.ArrayList;
 import java.util.List;
 import java.util.Scanner;

 public class POJ1006 {

     public static void main(String[] args) throws Exception {
         Scanner scanner = new Scanner(System.in);
         int t = 1;
         List<Long[]> aList = new ArrayList<Long[]>();
         List<Long> dList = new ArrayList<Long>();
         while(scanner.hasNext()){
             Long []a = {scanner.nextLong(),scanner.nextLong(),scanner.nextLong()};
             Long d = scanner.nextLong();
             if (a[0]==-1&&a[1]==-1&&a[2]==-1&&d==-1) {
                 break;
             }else {
                 aList.add(a);
                 dList.add(d);
             }
         }
         for (int i = 0; i < aList.size(); i++) {
             Long[] a = aList.get(i);
             long d = dList.get(i);
             Long[] m = { (long) 23, (long) 28, (long) 33 };
             long res = MyGcd.linearEquationGroup(a, m);
             while (res <= d) {
                 res += 21252;
             }
             System.out.println("Case " + (t++) + ": the next triple peak occurs in " + (res - d) + " days.");
         }
     }

     private static class MyGcd {
         static long x;
         static long y;

         /**
          *
          * @param a 余数组成的数组
          * @param m 模组成的数组
          * @return
          * @throws Exception
          */
         public static long linearEquationGroup(Long[] a, Long[] m) throws Exception {
             int len = a.length;
             if (len == 0 && a[0] == 0)
                 return m[0];

             for (int i = 1; i < len; i++) {
                 // 这里往前看是两个方程
                 long a2_a1 = a[i] - a[i - 1];
                 long d = linearEquation(m[i - 1], -m[i], a2_a1);
                 // 现在的x是y1,用y1求得一个特解
                 long x0 = a[i - 1] + m[i - 1] * x;
                 long lcm = m[i - 1] * m[i] / d;
                 a[i] = (x0 % lcm + lcm) % lcm;// x0变成正数
                 m[i] = lcm;
             }
             // 合并完之后,只有一个方程 : x = a[len-1] (% m[len-1])
             //long d = linearEquation(1, m[len-1], a[len-1]);
             return a[len - 1] % m[len - 1];
         }

         public static long inverseElement(long a, long mo) throws Exception {

             long d = linearEquation(a, mo, 1);
             x = (x % mo + mo) % mo;
             return d;
         }

         public static long linearEquation(long a, long b, long m) throws Exception {
             long d = ext_gcd(a, b);
             // m不是gcd(a,b)的倍数,这个方程无解
             if (m % d != 0)
                 throw new Exception("无解");
             long n = m / d;// 约一下,考虑m是d的倍数
             x *= n;
             y *= n;
             return d;
         }

         public static long ext_gcd(long a, long b) {

             if (b == 0) {
                 x = 1;
                 y = 0;
                 return a;
             }
             long res = ext_gcd(b, a % b);
             long x1 = x;// 备份x
             x = y;// 更新x
             y = x1 - a / b * y;// 更新y
             return res;
         }

     }

 }

　　结果：