第一节. .Net Core环境的安装和常用指令

一. 环境介绍和安装

1. 环境介绍

　.Net FrameWork框架：BCL(基础类库 system.dll)、CLR(运行时 仅支持：Windows)、FCL（一些框架，比如：MVC、WPF）

　.Net Core框架包括：BCL(基础类库)、CLR(运行时 分别有：Windows、MacOS、Linux的)、FCL（一些框架，比如：MVC）

　.Net Core Runtime == CLR

.Net Core SDK == CLR + 开发工具包(集成到VS里)

注：如果是单纯的是服务器为了部署.Net Core开发的项目，那么只需要安装 “.Net Core Runtime”即可；如果是本机电脑，既需要运行，还需要开发.Net Core的项目，那么就需要安装 .Net Core SDK。

2. 如何安装

(1). 可以下载支持不同系统的SDK和Runtime，进入官网：https://dotnet.microsoft.com/download，如下图：

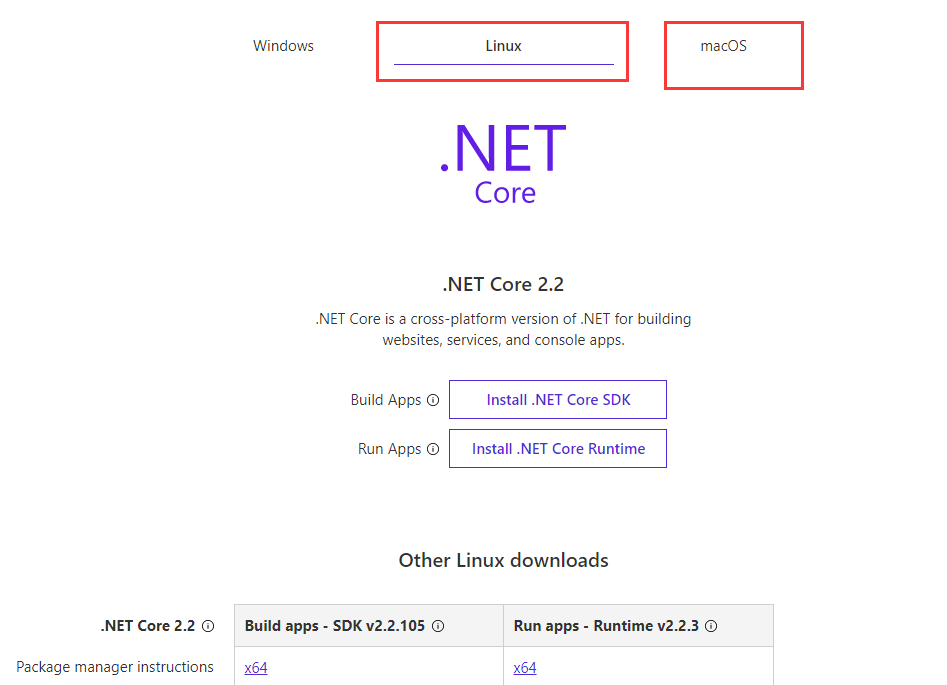
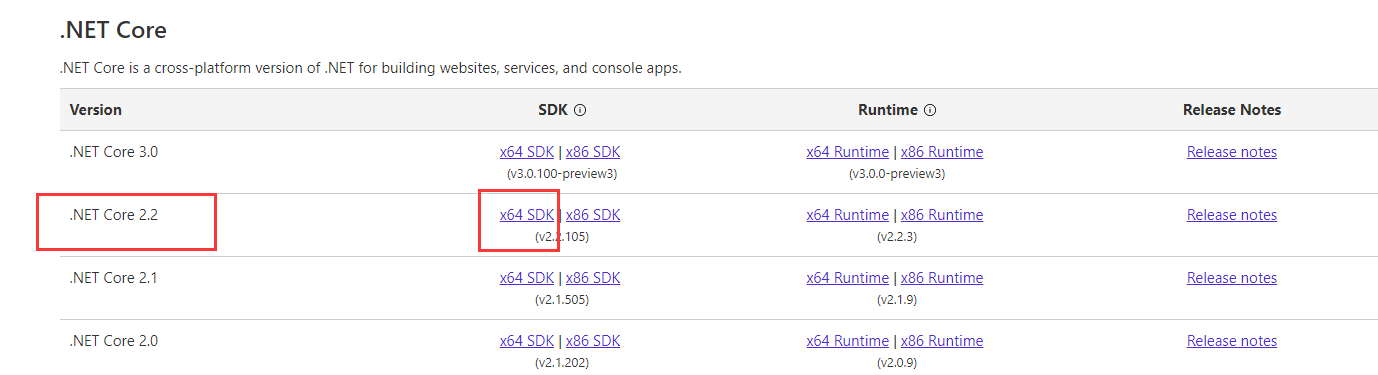
(2). 下载Windows下的.Net Core的SDK，进入微软的官方下载网站：https://dotnet.microsoft.com/download/visual-studio-sdks?utm_source=getdotnetsdk&utm_medium=referral，页面如下：这里以下载 .Net Core 2.2  64位的SDK为例。

(3). 下载下来exe程序，安装即可，安装成功如下图：

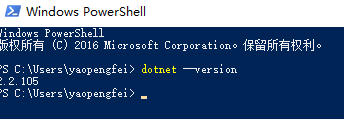
(4). 在命令行中，输入 【dotnet --version】，查看.Net Core的版本，如下图：

二. 常用指令

1. 在cmd命令行中输入【dotnet】，如下图： 

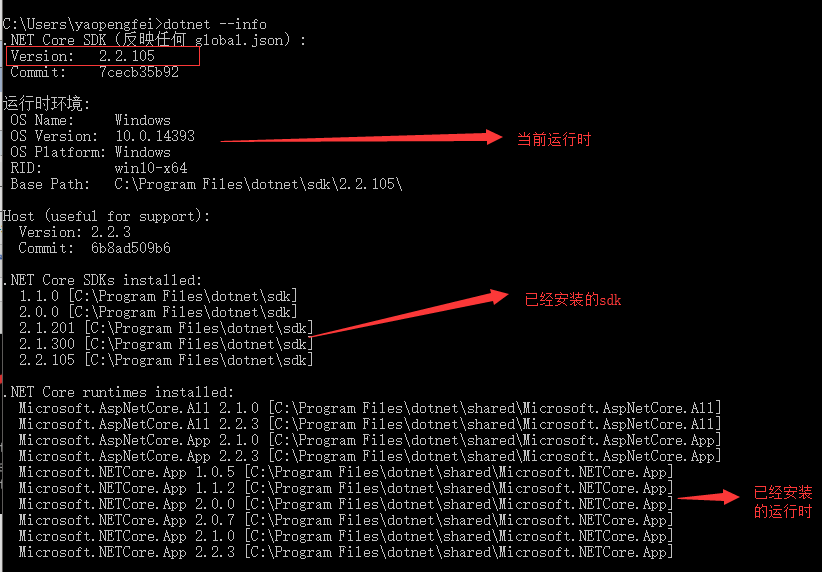
(1). 显示.Net Core的信息  【dotnet --info】，该指令已经包含了下面显示sdk和runtimes和当前版本信息了。

(2). 显示已经安装的SKD的信息 【dotnet --list-sdks】

(3). 显示已经安装的运行时的信息 【dotnet --list--runtimes】

(4). 显示当前.Net的版本 【dotnet --version】

(5). 帮助命令： 【dotnet -h】，如下图，引出很多新的命令，如new、run，如果想看某个指令的详细用法，eg： 【dotnet new --help】查看new指令的相关用法

2. 在cmd命令中输入【dotnet new --help】或者【dotnet new -h】

 小案例：

　　①：在桌面上新建一个名为“myMvc”的文件夹。

　　②：在该文件夹里新建一个mvc项目。

　　③：对该项目进行编译。

　　④：对该项目进行运行。

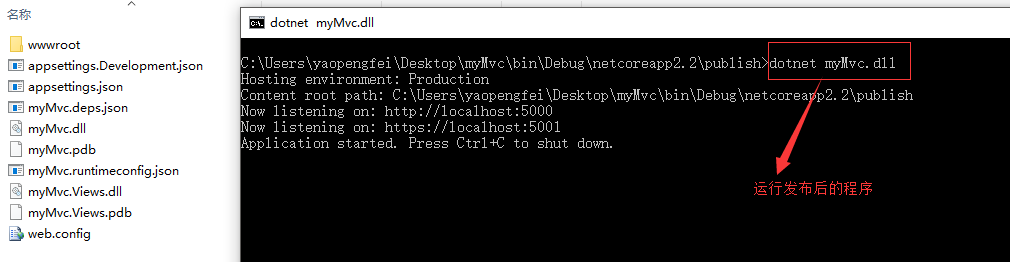
　　⑤：对该项目进行发布。

进入发布包路径，通过dotnet xx.dll运行即可。

!

• 作       者 : Yaopengfei(姚鹏飞)
• 博客地址 : http://www.cnblogs.com/yaopengfei/
• 声     明1 : 本人才疏学浅，用郭德纲的话说“我是一个小学生”，如有错误，欢迎讨论，请勿谩骂^_^。
• 声     明2 : 原创博客请在转载时保留原文链接或在文章开头加上本人博客地址，否则保留追究法律责任的权利。