隐马尔科夫模型（HMM）学习笔记二

　　这里接着学习笔记一中的问题2，说实话问题2中的Baum-Welch算法编程时矩阵转换有点烧脑，开始编写一直不对（编程还不熟练hh），后面在纸上仔细推了一遍，由特例慢慢改写才运行成功，所以代码里面好多处都有print。

　　笔记一中对于问题1（概率计算问题）采用了前向或后向算法，根据前向和后向算法可以得到一些后面要用到的概率与期望值。

一、问题2 学习问题已知观测序列，估计模型参数，使得在该模型下观测序列概率最大

　　隐马尔可夫模型的学习，根据训练数据除包括观测序列O外是否包括了对应的状态序列 I 分为监督学习和非监督学习。如果包括了状态序列 I ，则可以直接采用极大似然估计来估计隐马尔可夫模型的初始状态概率Pi，状态转移概率A和观测概率B（一般统计频数）。但是一般没有对应的状态序列 I ，如果人工标注训练数据的话代价太高，所以大多时候采用非监督学习方法------Baum-Welch算法。　

　　Baum-Welch算法

　　假设给定训练数据只包含S个长度为T的观测序列而没有对应的状态序列，目标是学习隐马尔可夫模型的参数。我们将观测序列数据看作观测数据O，状态序列数据看作不可观测的隐数据I，那么隐马尔可夫模型事实上是一个含有隐变量的概率模型

它的参数学习可以由EM算法实现（EM算法可以参考博客，博主写得通俗易懂）。

　　1、确定完全数据的对数似然函数

　　所有观测数据写成,所有隐数据写成，完全数据是。完全数据的对数似然函数是。

　　2、EM算法的E步：

　　求Q函数

其中，是隐马尔可夫模型参数的当前估计值，是要极大化的隐马尔可夫模型参数。（Q函数的标准定义是：，式子内部其实是条件概率，其中的对应；其与无关，所以省略掉了。）

于是函数可以写成：

式中求和都是对所有训练数据的序列总长度T进行的。这个式子是将代入后（取对数后变成加法，便于求解），将初始概率、转移概率、观测概率这三部分乘积的对数拆分为对数之和，所以有三项。

　　3、EM算法的M步:极大化Q函数求模型参数，由于要极大化的参数在Q函数表达式中单独地出现在3个项中，所以只需对各项分别极大化。

　　第1项可以写成：

注意到满足约束条件利用拉格朗日乘子法，写出拉格朗日函数：

对其求偏导数并令结果为0

得到

这个求导是很简单的，求和项中非i的项对πi求导都是0，logπ的导数是1/π，γ那边求导就剩下πi自己对自己求导，也就是γ。等式两边同时乘以πi就得到了上式。

对i求和得到γ：

代入中得到：

第2项可以写成：

类似第1项，应用具有约束条件的拉格朗日乘子法可以求出

第3项为:

同样用拉格朗日乘子法，约束条件是。注意，只有在对时对的偏导数才不为0,以表示。求得

　　Baum-Welch模型参数估计公式

　　将这三个式子中的各概率分别简写如下：

　　则可将相应的公式写成：

这三个表达式就是Baum-Welch算法（Baum-Welch algorithm)，它是EM算法在隐马尔可夫模型学习中的具体实现，由Baum和Welch提出。

　　算法 (Baum-Welch算法）

　　输入：观测数据

　　输出：隐马尔可夫模型参数。

　　(1)初始化。对,选取，得到模型。

　　(2)递推。对

右端各值按观测和模型计算。

　　(3)终止。得到模型参数。

　　分析：先根据前向算法得出alpha，根据后向算法得到beta，之后再根据本文最开始的公式计算gamma和sigamma矩阵，这里注意gamma是N*N维的，而sigamma是T-1*N*N维的，最后执行Baum-Welch算法。代码里面有相应的注释，这里我也卡了好久，可以先自己到纸上推一下。

def Baum_Welch(pi, A, B, obs_seq, error=0.005):

    switch = 0  # 判断是否停止迭代

    if not switch:

        N = A.shape[0]  # 可能的状态个数

        M = B.shape[1]  # 可能的观测结果个数

        T = len(obs_seq)  # 观测序列长度

        newB = np.zeros((N, M)) # 初始化观测概率

        alpha = forward_compute(pi, A, B, obs_seq)[1]   # 前向算法得到的alpha矩阵  N*T维

        print('alpha:', alpha)

        beta = backword_compute(pi, A, B, obs_seq)[1]   # 后向算法得到的beta矩阵  N*T维

        print('beta:', beta)

        gamma = np.zeros((N, T))  # gamma_t_i 表示t时刻在状态q_i的概率 N*N维

        sigamma = np.zeros((T-1, N, N))  # sigamma_t_i_j t时刻处于q_i,t+1时刻处于q_j的概率  (T-1)*N*N维

        for t in range(T-1):

            gamma[:, t] = (alpha[:, t]*beta[:, t]) / (alpha[:, t].dot(beta[:, t]))  # 求出gamma矩阵

            denom = np.dot(np.dot(alpha[:,t].T, A) * B[:,obs_seq[t+1]].T, beta[:,t+1])  # sigmma矩阵分母

            for i in range(N):

                molecule = alpha[i, t]* A[i,:] * B[:,obs_seq[t+1]]*beta[:,t+1]  # 分子

                sigamma[t,i,:] = molecule / denom   # 求sigamma

        gamma[:, T-1] = (alpha[:, T-1]*beta[:, T-1]) / (alpha[:, T-1].dot(beta[:, T-1]))  # 由于sigamma直到T-1,所以gamma最后要添加一列

        print('gamma:', gamma)

        print('sigamma:', sigamma)

        # print('-----------')

        # print(np.sum(sigamma, axis=0))

        # print('*********')

        # print(np.sum(gamma[:,:T-1], axis=1))

        # print(np.sum(gamma[:,:T-1], axis=1).reshape(N, -1))

        #更新

        newA = np.sum(sigamma, axis=0)/(np.sum(gamma[:,:T-1], axis=1).reshape(N, -1))

        # print(newA)

        # print(obs_seq==0)

        # print(np.sum(gamma, axis=1)

        for m in range(M):

            newB[:,m] = np.sum(gamma.T[obs_seq==m], axis=0)/(np.sum(gamma, axis=1))

        # print(newB)

        newpi = gamma[:, 0] 

        # 检查是否满足要求

        if np.max(abs(pi - newpi)) < error and np.max(abs(A - newA)) < error and np.max(abs(B - newB)) < error:

                switch = 1

        pi, A, B = newpi, newA, newB

    return A, B, pi

　　之后带入相关数据进行测试。

A = np.array([[0.1, 0.3, 0.6],[0.3, 0.5, 0.2], [0.3, 0.5, 0.2]])

B = np.array([[0.5, 0.5],[0.5, 0.5], [0.5,0.5]])

pi = np.array([0.2, 0.4, 0.4])

observations_data = np.array([0, 1, 0, 0, 1])

newA, newB, newpi = Baum_Welch(pi, A, B, observations_data)

print("newA: ", newA)

print("newB: ", newB)

print("newpi: ", newpi)

二、问题3 预测问题已知模型和观测序列，求给定序列最大概率下的状态

　　预测算法有两种：近似算法和维特比算法。

　　1.近似算法

　　基本思想：在每个时刻t选择在该时刻最有可能出现的状态 i^*_t ，从而得到一个状态序列 I^* = (i^*₁, i^*₂, ..., i^*_T)。

　　对于给定隐马尔可夫模型和观测序列O，在 t 时刻处于状态 qi 的概率gamma(i) 为：

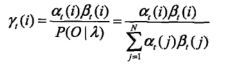
在每一时刻 t 最有可能的状态 i*t 为：

从而得到状态序列 I^* = (i^*₁, i^*₂, ..., i^*_T)。

这个代码很简单，直接对gamma按行求最大值就行。

'''

gamma: [[0.2     0.26    0.248   0.2504  0.44992]

        [0.4     0.46    0.448   0.2992  0.24992]

        [0.4     0.28    0.304   0.4504  0.30016]]

'''

def envolution_state(gamma):

    states = []

    for i in range(gamma.shape[1]):

        max_index = np.where(gamma==np.max(gamma[:,i]))[0][0]

        states.append(max_index)

    return states

print('*********test*********')

gamma = np.array([[0.2 ,0.26,0.248,0.2504,0.44992], [0.4,0.46,0.448,0.2992,0.24992], [0.4,0.28,0.304,0.4504,0.30016]])

print('state:', envolution_state(gamma))

　　2、维特比算法

　　基本思想：利用动态规划求解隐马尔科夫模型预测问题，即用动态规划求解概率最大路径（最优路径），一条路径对应一个状态序列。

　　算法(维特比算法）

　　输入：模型和观测;

　　输出：最优路径。

　　⑴初始化

　　(2)递推。对

　　(3)终止

　　(4)最优路径回溯。对

求得最优路径。

def vetebi(pi, A, B, obs_seq):

    N = A.shape[0]  # 状态个数

    T = len(obs_seq) # 观测序列长度

    deta = np.zeros((N, T))  # 初始化deta矩阵

    fia = np.zeros((N, T), dtype=int)  # 初始化fia矩阵

    path = np.zeros(T, dtype=int)  # 初始化最优路径

    deta[:, 0] = pi*B[:, obs_seq[0]]  # 计算deta_1

    for t in range(1, T):

        matrix = (deta[:, t-1]*A.T)*B[:, obs_seq[t]].reshape(N, -1)  # 计算乘法，deta按列取其中最大的

        deta[:, t] = np.max(matrix, axis=1)  # 给deta赋值

        fia[:, t] = np.argmax(matrix, axis=1)  # 给fia赋值，用于求最优路径

    print(deta)

    print(fia)

    # 最大概率

    P_max = np.max(deta[:, T-1])

    # print(P_max)

    # 求最优路径

    path[T-1] = np.max(fia[:, T-1])

    for t in range(T-2, -1, -1):

        path[t] = fia[:, t+1][path[t+1]]

    # print(path)

    return path+1

　　利用书本上例题进行测试。

# test

A = np.array([[0.5, 0.2, 0.3], [0.3, 0.5, 0.2], [0.2, 0.3, 0.5]])

B = np.array([[0.5, 0.5], [0.4, 0.6], [0.7, 0.3]])

pi = np.array([0.2, 0.4, 0.4])

obs_seq = np.array([0, 1, 0])

path = vetebi(pi, A, B, obs_seq)

print('the best path is :',path)