logistic回归学习

logistic回归是一种分类方法，用于两分类的问题，其基本思想为：

1. 寻找合适的假设函数，即分类函数，用来预测输入数据的结果；
2. 构造损失函数，用来表示预测的输出结果与训练数据中实际类别之间的偏差；
3. 最小化损失函数，从而获得最优的模型参数。

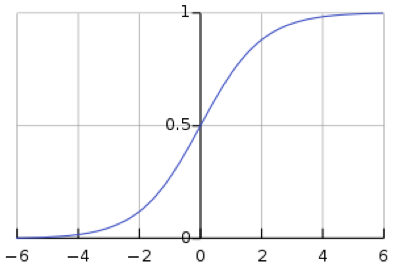
首先来看一下sigmoid函数：

\(g(x)=\frac{1}{1-e^{x}}\)

它的函数图像为：

logistic回归中的假设函数（分类函数）：

\(h_{\theta }(x)=g(\theta ^{T}x)=\frac{1}{1+e^{-\theta ^{T}x}}\)

解释：

\(\theta \) —— 我们在后面要求取的参数；

\(T\) —— 向量的转置，默认的向量都是列向量；

\(\theta ^{T}x\) —— 列向量\(\theta\)先转置，然后与\(x\)进行点乘，比如：

\(\begin{bmatrix}1\\ -1\\ 3\end{bmatrix}^{T}\begin{bmatrix}1\\ 1\\ -1\end{bmatrix} = \begin{bmatrix}1 & -1 & 3\end{bmatrix}\begin{bmatrix}1\\ 1\\ -1\end{bmatrix}=1\times 1+(-1)\times1+3\times(-1) = -3\)

logistic分类有线性边界和非线性边界两种：

线性边界形式为：\(\theta_{0}+\theta_{1}x_{1}+\cdots+\theta_{n}x_{n}=\sum_{i=0}^{n}\theta_{i}x_{i}=\theta^{T}x\)

非线性边界的形式为：\(\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+\theta_{3}x_{1}^{2}+\theta_{4}x_{2}^{2}\)

在概率上计算输入\(x\)结果为1或者0的概率分别为：

\(P(y=1|x;\theta)=h_{\theta}(x)\)

\(P(y=0|x;\theta)=1-h_{\theta}(x)\)

损失函数被定义为：\(J(\theta)=\frac{1}{m}\sum_{m}^{i=1}cost(h_{\theta}(x^{i}), y^{i})\)

其中：

这里\(m\)是所有训练样本的数目；

\(cost(h_{\theta}(x), y)=\left\{\begin{matrix}\ \ \ \ \ -log(h_{\theta}(x)) \ \ \ if\ y=1\\ -log(1-h_{\theta}(x)) \ \ \ if \ y=0\end{matrix}\right.\)

\(cost\)的另一种形式是：\(cost(h_{\theta}(x), y)=-y\times log(h_{\theta}(x))-(1-y)\times log(1-h_{\theta}(x))\)

将\(cost\)代入到\(J(\theta)\)中可以得到损失函数如下：

\(J(\theta)=-\frac{1}{m}[\sum_{m}^{i=1}y^{(i)}logh_{\theta}(x^{(i)})+(1-y^{(i)})log(1-h_{\theta}(x^{(i)}))]\)

梯度法求\(J(\theta)\)的最小值

\(\theta\)的更新过程如下：

\(\theta_{j}:=\theta_{j}-\alpha\frac{\partial }{\partial\theta_{j}}J(\theta),\ \ \ (j=0\cdots n)\)

其中：\(\alpha\)是学习步长。

\(\begin{align*} \frac{\partial }{\partial\theta_{j}}J(\theta) &= -\frac{1}{m}\sum_{m}^{i=1}\left ( y^{(i)}\frac{1}{h_{\theta}(x^{(i)})} \frac{\partial }{\partial\theta_{j}}h_{\theta}(x^{(i)})-(1-y^{(i)})\frac{1}{1-h_{\theta}(x^{(i)})}\frac{\partial }{\partial\theta_{j}}h_{\theta}(x^{(i)})\right )  \\  &=-\frac{1}{m}\sum_{m}^{i=1}\left ( y^{(i)}\frac{1}{g\left ( \theta^{T}x^{(i)} \right )}-\left ( 1-y^{(i)} \right )\frac{1}{1-g\left ( \theta^{T}x^{(i)} \right )} \right )\frac{\partial }{\partial\theta_{j}}g\left ( \theta^{T}x^{(i)} \right ) \\   &= -\frac{1}{m}\sum_{m}^{i=1}\left ( y^{(i)}\frac{1}{g\left ( \theta^{T}x^{(i)} \right )}-\left ( 1-y^{(i)} \right )\frac{1}{1-g\left ( \theta^{T}x^{(i)} \right )} \right ) g\left ( \theta^{T}x^{(i)} \right ) \left ( 1-g\left ( \theta^{T}x^{(i)} \right ) \right ) \frac{\partial }{\partial\theta_{j}}\theta^{T}x^{(i)} \end{align*}\)

\(\begin{align*} \frac{\partial }{\partial\theta_{j}}J(\theta) &= -\frac{1}{m}\sum_{m}^{i=1}\left ( y^{(i)}\left ( 1-g\left ( \theta^{T}x^{(i)} \right ) \right )-\left ( 1-y^{(i)} \right )g\left ( \theta^{T}x^{(i)}\right) \right )x_{j}^{\left (i  \right )} \\ &= -\frac{1}{m}\sum_{m}^{i=1}\left ( y^{(i)} -g\left ( \theta^{T}x^{(i)}\right) \right )x_{j}^{\left (i  \right )} \\ &=-\frac{1}{m}\sum_{m}^{i=1}\left ( y^{(i)} -h_{\theta}\left ( x^{(i)}\right) \right )x_{j}^{\left (i  \right )} \\&=\frac{1}{m}\sum_{m}^{i=1}\left ( h_{\theta}\left ( x^{(i)}\right)-y^{(i)} \right )x_{j}^{\left (i  \right )} \end{align*}\)

把偏导代入更新过程那么可以得到：

\(\theta_{j}:=\theta_{j}-\alpha\frac{1}{m}\sum_{m}^{i=1}\left ( h_{\theta}\left ( x^{(i)}\right)-y^{(i)} \right )x_{j}^{\left (i  \right )}\)

学习步长\(\alpha\)通常是一个常量，然后省去\(\frac{1}{m}\)，可以得到最终的更新过程：

\(\theta_{j}:=\theta_{j}-\alpha\sum_{m}^{i=1}\left ( h_{\theta}\left ( x^{(i)}\right)-y^{(i)} \right )x_{j}^{\left (i  \right )}, \ \ \ \ \left ( j=0\cdots n \right )\)

向量化梯度

训练样本用矩阵来描述就是：

\(X= \begin{bmatrix} x^{(1)}\\ x^{(2)}\\ \cdots \\ x^{(m)}\end{bmatrix}=\begin{bmatrix} x_{0}^{(1)} & x_{1}^{(1)} & \cdots & x_{n}^{(1)}\\ x_{0}^{(2)} & x_{1}^{(2)} & \cdots & x_{n}^{(2)}\\ \cdots & \cdots & \cdots & \cdots \\  x_{0}^{(m)} & x_{1}^{(m)} & \cdots & x_{n}^{(m)} \end{bmatrix}, \ \ Y=\begin{bmatrix} y^{\left ( 1 \right )}\\  y^{\left ( 2 \right )}\\  \cdots \\ y^{\left ( m \right )}\end{bmatrix}\)

参数\(\theta\)的矩阵形式为：

\(\Theta=\begin{bmatrix} \theta^{\left ( 1 \right )}\\  \theta^{\left ( 2 \right )}\\  \cdots \\ \theta^{\left ( m \right )}\end{bmatrix}\)

先计算\(X\cdot \Theta\)，并记结果为\(A\)：

\(A=X\cdot\Theta\)，其实就是矩阵的乘法

再来求取向量版的误差\(E\)：

\(E=h_{\Theta}\left ( X \right )-Y=\begin{bmatrix} g\left ( A^{1} \right )-y^{\left (1  \right )}\\ g\left ( A^{1} \right )-y^{\left (1  \right )}\\  \cdots \\  g\left ( A^{1} \right )-y^{\left (1  \right )}\end{bmatrix} = \begin{bmatrix} e^{(1)}\\ e^{(2)}\\ \cdots \\ e^{(m)}\end{bmatrix}\)

当\(j=0\)时的更新过程为：

\(\begin{align*} \theta_{0}&=\theta_{0}-\alpha\sum_{m}^{i=1}\left ( h_{\theta}\left ( x^{(i)}\right)-y^{(i)} \right )x_{0}^{\left (i  \right )}, \ \ \ \ \left ( j=0\cdots n \right ) \\  &= \theta_{0}-\alpha\sum_{m}^{i=1}e^{\left ( i \right )}x_{0}^{\left ( i \right )} \\ &= \theta_{0}-\alpha \begin{bmatrix} x_{0}^{\left ( 1 \right )} & x_{0}^{\left ( 2 \right )} & \cdots & x_{m}^{\left ( 0 \right )} \end{bmatrix} \cdot E \end{align*}\)

对于\(\theta_{j}\)同理可以得到：

\(\theta_{j} = \theta_{j}-\alpha \begin{bmatrix} x_{j}^{\left ( 1 \right )} & x_{j}^{\left ( 2 \right )} & \cdots & x_{j}^{\left ( m \right )} \end{bmatrix} \cdot E\)

用矩阵来表达就是：

\(\begin{align*}\begin{bmatrix} \theta_{0}\\ \theta_{1}\\ \cdots \\ \theta_{n}\end{bmatrix} &= \begin{bmatrix} \theta_{0}\\ \theta_{1}\\ \cdots \\ \theta_{n}\end{bmatrix} - \alpha \cdot \begin{bmatrix} x_{0}^{\left ( 1 \right )} & x_{0}^{\left ( 2 \right )} & \cdots & x_{0}^{\left (m \right )}\\  x_{1}^{\left ( 1 \right )} & x_{1}^{\left ( 2 \right )} & \cdots & x_{1}^{\left (m \right )}\\ \cdots & \cdots  &  \cdots &  \cdots\\ x_{n}^{\left ( 1 \right )} & x_{n}^{\left ( 2 \right )} & \cdots & x_{n}^{\left (m \right )}\\ \end{bmatrix} \cdot E \\  &= \theta - \alpha \cdot x^{T} \cdot E \end{align*}\)

以上就三个步骤：

1. 求取模型的输出：\(A=X \cdot \Theta\)

2. sigmoid映射之后求误差：\(E=g\left ( A \right )-Y\)

3. 利用推导的公式更新\(\Theta\)，\(\Theta:=\Theta-\alpha \cdot X^{T} \cdot E\)，然后继续回到第一步继续。