洛谷P2698 花盆Flowerpot【单调队列】

题目描述

Farmer John has been having trouble making his plants grow, and needs your help to water them properly. You are given the locations of N raindrops (1 <= N <= 100,000) in the 2D plane, where y represents vertical height of the drop, and x represents its location over a 1D number line:

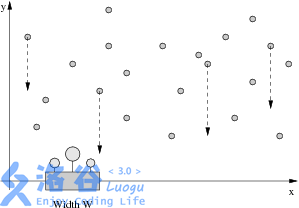
Each drop falls downward (towards the x axis) at a rate of 1 unit per second. You would like to place Farmer John's flowerpot of width W somewhere along the x axis so that the difference in time between the first raindrop to hit the flowerpot and the last raindrop to hit the flowerpot is at least some amount D (so that the flowers in the pot receive plenty of water). A drop of water that lands just on the edge of the flowerpot counts as hitting the flowerpot.

Given the value of D and the locations of the N raindrops, please compute the minimum possible value of W.

老板需要你帮忙浇花。给出N滴水的坐标，y表示水滴的高度，x表示它下落到x轴的位置。

每滴水以每秒1个单位长度的速度下落。你需要把花盆放在x轴上的某个位置，使得从被花盆接着的第1滴水开始，到被花盆接着的最后1滴水结束，之间的时间差至少为D。

我们认为，只要水滴落到x轴上，与花盆的边沿对齐，就认为被接住。给出N滴水的坐标和D的大小，请算出最小的花盆的宽度W。

输入输出格式

输入格式：

第一行2个整数 N 和 D。

第2.. N+1行每行2个整数，表示水滴的坐标(x,y)。

输出格式：

仅一行1个整数，表示最小的花盆的宽度。如果无法构造出足够宽的花盆，使得在D单位的时间接住满足要求的水滴，则输出-1。

输入输出样例

输入样例#1： 复制

4 5
6 3
2 4
4 10
12 15

输出样例#1： 复制

2

说明

【样例解释】

有4滴水， (6,3), (2,4), (4,10), (12,15).水滴必须用至少5秒时间落入花盆。花盆的宽度为2是必须且足够的。把花盆放在x=4..6的位置，它可以接到1和3水滴, 之间的时间差为10-3 = 7满足条件。

【数据范围】

40%的数据：1 ≤ N ≤ 1000，1 ≤ D ≤ 2000；

100%的数据：1 ≤ N ≤ 100000，1 ≤ D ≤ 1000000，0≤x,y≤10^6。

题意：

用一个宽度最小的花盆接雨滴，使得这个区间内的雨滴的纵坐标最大值和最小值之差大于等于d

思路：

一眼思路是用线段树维护区间最大值和最小值，二分答案。当然T了，而且WA，才拿了20分。好菜啊。

讲道理顶多会T，怎么会WA呢我好菜啊哭。

 #include <iostream>
 #include <set>
 #include <cmath>
 #include <stdio.h>
 #include <cstring>
 #include <algorithm>
 #include <vector>
 #include <queue>
 #include <map>
 #include <bits/stdc++.h>
 using namespace std;
 typedef long long LL;
 #define inf 0x7f7f7f7f

 const int maxn = 1e5 + ;
 const int maxd = 1e6 + ;
 int n, d, mmx, mmin;
 int height[maxd];
 int tree_max[maxd << ], tree_min[maxd << ];

 void pushup(int rt)
 {
     tree_max[rt] = max(tree_max[rt << ], tree_max[rt <<  | ]);
     tree_min[rt] = min(tree_min[rt << ], tree_min[rt <<  | ]);
 }

 void build(int rt, int l, int r)
 {
     if(l == r){
         if(height[l] == -){
             tree_max[rt] = -inf;
             tree_min[rt] = inf;
         }
         else{
             tree_max[rt] = tree_min[rt] = height[l];
         }
         return;
     }
     int mid = (l + r) / ;
     build(rt << , l, mid);
     build(rt <<  | , mid + , r);
     pushup(rt);
 }

 int query_max(int L, int R, int l, int r, int rt)
 {
     if(L <= l && R >= r){
         return tree_max[rt];
     }
     int mid = (l + r) / ;
     int res = -inf;
     if(L <= mid){
         res = max(res, query_max(L, R, l, mid, rt << ));
     }
     if(R > mid){
         res = max(res, query_max(L, R, mid + , r, rt <<  | ));
     }
     return res;
 }

 int query_min(int L, int R, int l, int r, int rt)
 {
     if(L <= l && R >= r){
         return tree_min[rt];
     }
     int mid = (l + r) / ;
     int res = inf;
     if(L <= mid){
         res = min(res, query_min(L, R, l, mid, rt << ));
     }
     if(R > mid){
         res = min(res, query_min(L, R, mid + , r, rt <<  | ));
     }
     return res;
 }

 bool check(int len)
 {
     for(int i = mmin; i <= mmx; i++){
         //cout<<query_max(i, i + len, 1, mmx, 1)<<endl;
         //cout<<query_min(i, i + len, 1, mmx, 1)<<endl;
         if(query_max(i, i + len, , mmx, ) - query_min(i, i + len, , mmx, ) >= d)return true;
     }
     return false;
 }

 int main()
 {
     scanf("%d%d", &n, &d);
     mmx = -inf;
     mmin = inf;
     memset(tree_max, -inf, sizeof(tree_max));
     memset(tree_min, inf, sizeof(tree_min));
     memset(height, -, sizeof(height));
     for(int i = ; i < n; i++){
         int x, y;
         scanf("%d%d", &x, &y);
         height[x] = y;
         mmx = max(mmx, x);
         mmin = min(mmin, x);
     }

     build(, , mmx);

     int ans = -, st = mmin, ed = mmx;
     while(st <= ed){
         int mid = (st + ed) / ;
         if(check(mid)){
             ed = mid - ;
             ans = mid;
         }
         else{
             st = mid + ;
         }
     }

     printf("%d\n", ans);
     return ;
 }

好吧既然是单调队列专题，就去学习一下单调队列吧。

其实刚开始想到了如果加入了一个雨滴之后，他和队头的高度差小于前面的，并且距离差也变大了的话，那这个雨滴肯定是没用的。之后就不会了。

应该要想到的是，当我们加入了一个雨滴之后，这一段的最大值只有可能增大或不变，最小值只有可能减小或者不变。他们都是单调的。

可以用一个单调队列来维护最大最小值，队头元素是最小值，队尾元素是最大值。

先按照横坐标对雨滴排个序，然后一个个加入，当队头和队尾纵坐标之差大于等于d的时候就把队头丢掉。因为之后加入队列的那个元素和队头虽然也会满足大于等于d但是宽度就不是最小的了。

但是这样只是找到了从左到右的一个单调序列，还应该再考虑一下从右到左。其实就相当于纪要考虑从左到右递增的，也要考虑从左到右递减的。

虽然这道题数据有问题，只考虑从左到右也能AC

 #include <iostream>
 #include <set>
 #include <cmath>
 #include <stdio.h>
 #include <cstring>
 #include <algorithm>
 #include <vector>
 #include <queue>
 #include <map>
 #include <bits/stdc++.h>
 using namespace std;
 typedef long long LL;
 #define inf 0x7f7f7f7f

 const int maxn = 1e5 + ;
 const int maxd = 1e6 + ;
 int n, d, mmx, mmin;
 int height[maxd];

 struct node{
     int x, y;
 }drop[maxn], que1[maxn], que2[maxn];

 bool cmp(node a, node b)
 {
     return a.x < b.x;
 }

 int main()
 {
     scanf("%d%d", &n, &d);
     for(int i = ; i < n; i++){
         scanf("%d%d", &drop[i].x, &drop[i].y);
     }
     sort(drop, drop + n, cmp);

     int tail = , head = , ans = inf;
     for(int i = ; i < n; i++){
         while(que1[tail].y >= drop[i].y && head <= tail)tail--;
         que1[++tail] = drop[i];
         //cout<<"head"<<que[head].x<<" tail"<<que[tail].x<<endl;
         while(que1[tail].y - que1[head].y >= d){
             ans = min(ans, que1[tail].x - que1[head].x);
             head++;
         }
     }
     //cout<<ans<<endl;
     tail = ;
     head = ;
     for(int i = n - ; i >= ; i--){
         while(que2[tail].y >= drop[i].y && head <= tail)tail--;
         que2[++tail] = drop[i];
         while(que2[tail].y - que2[head].y >= d){
             ans = min(ans, que2[head].x - que2[tail].x);
             head++;
         }
     }

     if(ans == inf){
         printf("-1\n");
     }
     else{
         printf("%d\n", ans);
     }
     return ;
 }