codeforces 894B - Ralph And His Magic Field - [数学题]
题目链接:https://cn.vjudge.net/problem/CodeForces-894B
Ralph has a magic field which is divided into n × m blocks. That is to say, there are n rows and m columns on the field. Ralph can put an integer in each block. However, the magic field doesn't always work properly. It works only if the product of integers in each row and each column equals to k, where k is either 1 or -1.
Now Ralph wants you to figure out the number of ways to put numbers in each block in such a way that the magic field works properly. Two ways are considered different if and only if there exists at least one block where the numbers in the first way and in the second way are different. You are asked to output the answer modulo 1000000007 = 109 + 7.
Note that there is no range of the numbers to put in the blocks, but we can prove that the answer is not infinity.
Input
The only line contains three integers n, m and k (1 ≤ n, m ≤ 1018, k is either 1 or -1).
Output
Print a single number denoting the answer modulo 1000000007.
Example
1 1 -1
1
1 3 1
1
3 3 -1
16
Note
In the first example the only way is to put -1 into the only block.
In the second example the only way is to put 1 into every block.
题意:
给出一个n*m的方格矩阵,给定k=-1或1,在所有方格里面填上-1或1,使得每行每列的乘积都为k,则算作一种方案,求总共有多少种不同方案。
题解:
①当n+m为奇数,k=-1时,方案数=0;
因为这时,n和m必然为一奇一偶,不妨设n为奇数,m为偶数;
则在每一行上必然要放奇数个-1,那么这样可以知道-1的总个数是偶数(奇数行,每行奇数个-1);
但是,同时每一列上也要放奇数个-1,那么-1的总个数是奇数(偶数列,每列奇数个-1);
互相矛盾,所以不存在这样的方案。
②其他情况下,存在至少一种方案,此时我们设有矩阵A[n][m]:
a[1][1] …………………… a[1][m-1] a[1][m]
……………………………………………………
……………………………………………………
a[n-1][1] ……………… a[n-1][m-1] a[n-1][m]
a[n][1] …………………… a[n][m-1] a[n][m]
此时矩阵A[n-1][m-1]里面可以随意填入1或者-1,则对应的 a[n][1] ~ a[n-1][m] 和 a[1][m] ~ a[n-1][m] 需要取-1或者1来使得行列为k;
例如: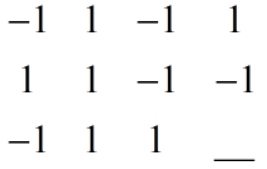 ,因为
,因为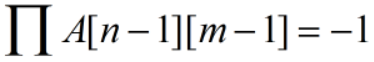 ,所以
,所以 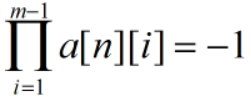 和
和 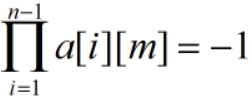 ,所以a[n][m]存在,所以方案存在。
,所以a[n][m]存在,所以方案存在。
因此我们不能难算出方案数为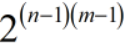 ;
;
AC代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll MOD = ;
ll n,m;int k;
ll fpow(ll a,ll b){//快速幂
ll r=,base=a%MOD;
while(b){
if(b&) r*=base , r%=MOD;
base*=base;
base%=MOD;
b>>=;
}
return r;
}
int main()
{
cin>>n>>m>>k;
if(k==- && (n+m)%==)
{
printf("0\n");
return ;
} ll ans=fpow(,n-);
ans=fpow(ans,m-);
cout<<ans<<endl;
}
PS.显然最大10^18数量级的n和m直接乘起来肯定爆炸longlong,所以分两次快速幂即可。
PS2.此处#include<bits/stdc++.h>的话,因为包含进了pow()函数,这样我们就要给快速幂函数改个名字(比如fpow……),避免错误。
codeforces 894B - Ralph And His Magic Field - [数学题]的更多相关文章
- Codeforces 894B - Ralph And His Magic Field
894B - Ralph And His Magic Field 思路: 当k为1时,如果n和m奇偶性不同,那么没有答案. 可以证明,在其他情况下有答案,且答案为2^(n-1)*(m-1),因为前n- ...
- codeforces #447 894A QAQ 894B Ralph And His Magic Field 894C Marco and GCD Sequence
A.QAQ 题目大意:从给定的字符串中找出QAQ的个数,三个字母的位置可以不连续 思路:暴力求解,先找到A的位置,往前扫,往后扫寻找Q的个数q1,q2,然 后相乘得到q1*q2,这就是这个A能够找到的 ...
- Codeforces 894.B Ralph And His Magic Field
B. Ralph And His Magic Field time limit per test 1 second memory limit per test 256 megabytes input ...
- Codeforces Round #447 (Div. 2) B. Ralph And His Magic Field【数论/组合数学】
B. Ralph And His Magic Field time limit per test 1 second memory limit per test 256 megabytes input ...
- Codeforces Round #447 (Div. 2) B. Ralph And His Magic Field 数学
题目链接 题意:给你三个数n,m,k;让你构造出一个nm的矩阵,矩阵元素只有两个值(1,-1),且满足每行每列的乘积为k,问你多少个矩阵. 解法:首先,如果n,m奇偶不同,且k=-1时,必然无解: 设 ...
- 【Codeforces Round #447 (Div. 2) B】Ralph And His Magic Field
| [链接] 我是链接,点我呀:) [题意] 给你一个n*m矩阵,让你在里面填数字. 使得每一行的数字的乘积都为k; 且每一列的数字的乘积都为k; k只能为1或-1 [题解] 显然每个位置只能填1或- ...
- CF894B Ralph And His Magic Field
题目链接:http://codeforces.com/contest/894/problem/B 题目大意: 往一个 \(n \times m\) 的网格中填数字 \((1 \le n,m \le 1 ...
- codeforces #369div2 B. Chris and Magic Square
题目:在网格某一处填入一个正整数,使得网格每行,每列以及两条主对角线的和都相等 题目链接:http://codeforces.com/contest/711/problem/B 分析:题目不难,找到要 ...
- codeforces 711B B. Chris and Magic Square(水题)
题目链接: B. Chris and Magic Square 题意: 问在那个空位子填哪个数可以使行列对角线的和相等,就先找一行或者一列算出那个数,再验证是否可行就好; AC代码: #include ...
随机推荐
- 定时器Enable Disable控制
问题:定时器如何控制它一会可用一会不可用,根据某个业务需求,比如:一个控制台程序扫描表中某个条件的数据,处理数据,控制台分布式部署,当主机宕机后,从机扫描定时器需要可用,当主机复活后,从机的扫描定时器 ...
- 8 -- 深入使用Spring -- 3...2 ResouceLoader 接口和 ResourceLoaderAware 接口
8.3.2 ResouceLoader 接口和 ResourceLoaderAware 接口 Spring 提供如下两个标志性接口: ⊙ ResourceLoader : 该接口实现类的实例可以获得一 ...
- NetBpm 示例:请假审批(6)
转载注明出处: http://www.cnblogs.com/anbylau2130/p/3877983.html 原文: 请假示例 流程定义包源码下载(注:par包就是zip格式压缩包).原文地址: ...
- Python中的类(中)
上一篇介绍了Python中类相关的一些基本点,本文看看Python中类的继承和__slots__属性. 继承 在Python中,同时支持单继承与多继承,一般语法如下: class SubClassNa ...
- 【PHP】phpstudy vhosts.conf 配置
#Listen 876 <VirtualHost *:876> ServerName localhost DocumentRoot "D:\phpStudy\PHPTutoria ...
- Oracle查询锁表和解锁
1.查询是否锁表 SELECT l.session_id sid, s.serial#, l.locked_mode,l.oracle_username, l.os_user_name,s.machi ...
- RabbitMQ之总结
P:生成者,消息产生者: C:消息消费者: 红:消息队列: java实现 步骤: 创建连接 从连接中创建通道(相当于JDBC中的Statement) 通过channel声明(创建)队列.(如果队列存在 ...
- Ubuntu下Eclipse的安装方法
1. 下载jre,eclipse,cdt 其中jre是java运行环境,eclipse需要先装jre,才可能运行,cdt是在eclipse中运行c\c++程序的插件. 1.1 下载jre 网址是:ja ...
- ajax劫持?
<html<meta http-equiv="Content-Type" content="application/xhtml+xml; charset=ut ...
- Form表单验证神器: BootstrapValidator
前言:做Web开发的我们,表单验证是再常见不过的需求了.友好的错误提示能增加用户体验.博主搜索bootstrap表单验证,搜到的结果大部分都是文中的主题:bootstrapvalidator.今天就来 ...
