HDU 3507 - Print Article - [斜率DP]

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=3507

Zero has an old printer that doesn't work well sometimes. As it is antique, he still like to use it to print articles. But it is too old to work for a long time and it will certainly wear and tear, so Zero use a cost to evaluate this degree. 
One day Zero want to print an article which has N words, and each word i has a cost Ci to be printed. Also, Zero know that print k words in one line will cost

M is a const number. 
Now Zero want to know the minimum cost in order to arrange the article perfectly. 

Input

There are many test cases. For each test case, There are two numbers N and M in the first line (0 ≤ n ≤ 500000, 0 ≤ M ≤ 1000). Then, there are N numbers in the next 2 to N + 1 lines. Input are terminated by EOF.

Output

A single number, meaning the mininum cost to print the article.

Sample Input

5 5
5
9
5
7
5

Sample Output

230

题意：

假设一篇文章有N个词，每个词有c[i]代表花费；

现在打印文章，打印一行需要花费 M + ( ∑c[i] )²，求怎么打印整篇文章花费最少，为多少。

题解：

假设dp[i]代表输出前i个词的最小费用，那么就有状态转移方程：

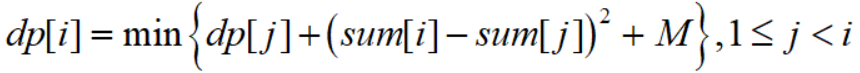
sum[i]代表前i个词的c[i]之和；

状态转移方程的意思也很明显，就是枚举选出第i个单词所在的那一行上打印多少个单词最优；

那么如果直接求解的话，O(n²)的时间复杂度对于n=500000的规模是超时的，所以就要使用斜率优化：

那么当我们计算dp[i]时，假设有 1 <= k < j < i，如果有：

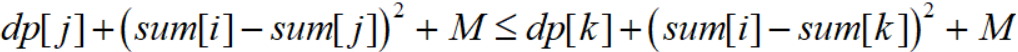
就可以说j点比k点更优。

对上式进行变形可得：

我们设

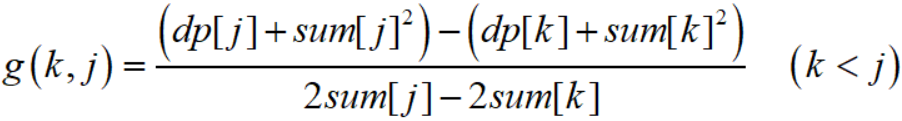
那么就有：（在计算dp[i]时）j点比k点优  ↔  g(k,j) ≤ sum[i]；……………………(1)

　　　　　　　　　　　　　 j点比k点差  ↔  g(k,j) > sum[i]；……………………(2)

（这就像，g(k,j)代表k点与j点的连线斜率，这个斜率小于某个阈值就j更优，否则就k更优）

就不难得到：

①在计算dp[i]时，若有1≤a<b<c<i，只要满足g(a,b) ≥ g(b,c)，则b点必然被淘汰.　　（注意此处的g(a,b) ≥ g(b,c)是必须是要取到等号的）

证明：若g(b,c) ≤ sum[i]，由(1)得c点优于b点，选择c点；

　　　若g(b,c) > sum[i]，则g(a,b) ≥ g(b,c) > sum[i]，由(2)得a点比b点更优，选择a点；

　　　最终，怎么样都选不到b点，故b点必然淘汰。

②若在计算dp[i]时，k点被淘汰，则计算dp[i+1]时，k点必然也被淘汰.

证明：当k点被淘汰，即必然有一点j比k更优，则g(k,j) ≤ sum[i]，由于c[i] > 0，则g(k,j) ≤ sum[i] < sum[i+1]，即计算dp[i+1]时，j依然比k更优，k依然淘汰。

因此我们可以考虑维护一个斜率的队列来优化整个DP过程：

1、求解dp[i]：

　　假设队列中的头部依次存在元素a,b，且g(a,b) ≤ sum[i]，则b点比a点优，于是a淘汰出队；

　　重复上述操作，直到队列元素个数小于2或者g(a,b) > sum[i]。

　　最后dp[i]=getDP(Q[head])。

2、入队点i：

　　假设队列中的尾部依次存在元素a,b，那么当点c要入队的时候，如果g(a,b) > g(b,c)，那么就将b点删除；

　　重复上述操作，直到队列元素个数小于2，或者找到x,y能满足g(x,y) ≤ g(y,c)，将d点加入在该位置中。

AC代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn=;

int n,m,sum[maxn];
int dp[maxn];
int q[maxn],head,tail; //数组模拟队列

int getDP(int i,int j){return dp[j]+(sum[i]-sum[j])*(sum[i]-sum[j])+m;}

int gUp(int k,int j){return (dp[j]+sum[j]*sum[j])-(dp[k]+sum[k]*sum[k]);} //g(k,j)的分子部分
int gDown(int k,int j){return *(sum[j]-sum[k]);} //g(k,j)的分母部分

int main()
{
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        sum[]=;
        for(int i=,tmp;i<=n;i++)
        {
            scanf("%d",&tmp);
            sum[i]=sum[i-]+tmp;
        }

        dp[]=;
        head=tail=;
        q[tail++]=;
        for(int i=;i<=n;i++)
        {
            //计算dp[i]
            while(tail-head>= && gUp(q[head],q[head+])<=sum[i]*gDown(q[head],q[head+]))
                head++;
            dp[i]=getDP(i,q[head]);

            //入队点i
            while(tail-head>= && gUp(q[tail-],q[tail-])*gDown(q[tail-],i)>=gUp(q[tail-],i)*gDown(q[tail-],q[tail-]))
                tail--;
            q[tail++]=i;
        }

        printf("%d\n",dp[n]);
    }
}

有一点需要注意的是，本题中c[i]其实是有可能等于0的，所以不能直接gUp/gDown，而是要把分母gDown乘到其另一边再进行比较。

刚开始头铁，强行用list来模拟本题的队列，写*Q.begin()和*++Q.begin()和*Q.end()和*--Q.end()丑的一B，

强行写完之后，发现因为耗时O(size)的size()方法超时，定义一个_size变量代替之后发现确实还是不如直接数组模拟快，

更严重的是，用list写法并没有简单好看多少，最后还是老老实实数组模拟队列吧……