多项式函数插值：全域多项式插值（一）单项式基插值、拉格朗日插值、牛顿插值 [MATLAB]

　　全域多项式插值指的是在整个插值区域内形成一个多项式函数作为插值函数。关于多项式插值的基本知识，见“计算基本理论”。

　　在单项式基插值和牛顿插值形成的表达式中，求该表达式在某一点处的值使用的Horner嵌套算法啊，见"Horner嵌套算法"。

1. 单项式(Monomial)基插值

1）插值函数基　　单项式基插值采用的函数基是最简单的单项式：$$\phi_j(t)=t^{j-1}, j=1,2,...n;\quad f(t)=p_{n-1}(t)=x_1+x_2t+x_3t^2+...x_nt^{n-1}=\sum\limits_{j=1}^nx_jt^{j-1}$$　　所要求解的系数即为单项式系数 $x_1,x_2,...x_n$ ，在这里仍然采用1,2,...n的下标记号而不采用和单项式指数对应的0,1,2,...,n-1的下标仅仅是出于和前后讨论一致的需要。

2）叠加系数

　　单项式基插值采用单项式函数基，若有m个离散数据点需要插值，设使用n项单项式基底：

$$x_1+t_1x_2+t_1^2x_3+...+t_1^{n-1}x_n=y_1\\ x_1+t_2x_2+t_2^2x_3+...+t_2^{n-1}x_n=y_2\\ ......   ......   ......   ......   ......   ......\\ x_1+t_mx_2+t_m^2x_3+...+t_m^{n-1}x_n=y_m$$　　系数矩阵为一 $m\times n$ 的矩阵($m\leq n$)，范德蒙(Vandermonde)矩阵：

$$\begin{bmatrix}1&t_1&t_1^2&...&t_1^{n-1}\\1&t_2&t_2^2&...&t_2^{n-1}\\...&...&...&...&...\\1&t_n&t_n^2&...&t_n^{n-1}\end{bmatrix} \begin{bmatrix}x_1\\x_2\\...\\x_n\end{bmatrix}=\begin{bmatrix}y_1\\y_2\\...\\y_n\end{bmatrix}$$　　根据计算基本理论中的讨论，多项式插值的函数基一定线性无关，且只要离散数据点两两不同，所构成的矩阵行也一定线性无关，这保证了矩阵一定行满秩。此时当且仅当m=n时，叠加系数有且仅有一组解。因此，n=插值基底的个数=离散数据点的个数=多项式次数+1。

3）问题条件和算法复杂度

　　生成范德蒙矩阵的复杂度大致在 $O(n^2)$ 量级；由于范德蒙矩阵并没有什么好的性质，既没有稀疏性，也没有对称性，因此只能使用标准的稠密矩阵分解（如LU）来解决，复杂度在 $O(n^3)$ 量级。因此，问题的复杂度在 $O(n^3)$ 量级。

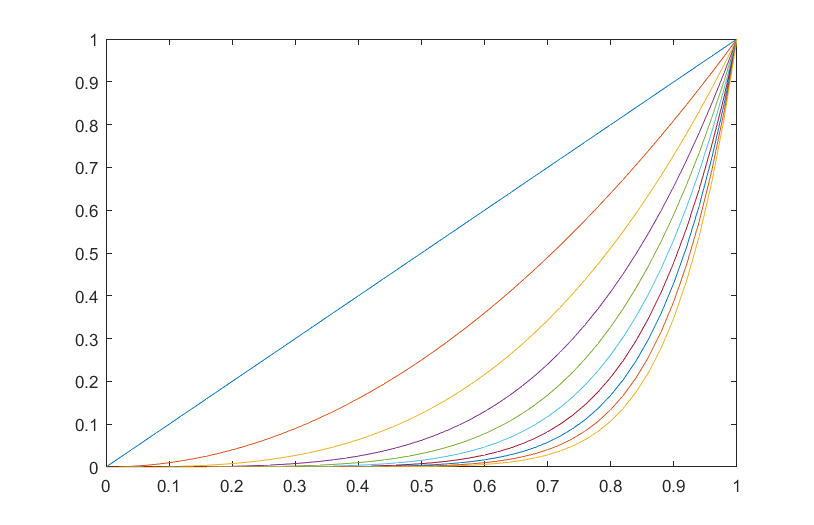
　　范德蒙矩阵存在的问题是，当矩阵的维数越来越高的时候，解线性方程组时问题将越来越病态，条件数越来越大；从另一个角度来说，单项式基底本身趋势相近，次数增大时将越来越趋于平行（见下图）。这将造成随着数据点的增加，确定的叠加系数的不确定度越来越大，因此虽然单项式基很简单，进行插值时却往往不用这一方法。如果仍然采用单项式基底，有时也会进行两种可以改善以上问题的操作：平移(shifting)和缩放(scaling)，即将 $((t-c)/d)^{j-1}$ 作为基底。常见的平移和缩放将所有数据点通过线性变换转移到区间[-1,1]中，即：$c=(t_1+t_n)/2,d=(t_n-t_1)/2$ 。

4）算法实现 

　　使用MATLAB实现单项式插值代码如下：

function [ polyfunc, vecx, condition ] = MonoPI( vect, vecy, shift, scale )
%    计算单项式型插值多项式系数
%    输入四个参数：插值点行向量vect，插值点函数值行向量vecy，平移shift，压限scale；
%    输出两个参数：插值多项式各项系数行向量vecx，矩阵条件数condition；

% 设置缺省值：若只输入两个参数，则不平移不缩放
if nargin==2
    shift = 0; scale = 1;
end

% 求解系数
vecsize = size(vect, 2);
basis = (vect - shift * ones(1, vecsize))/scale;    % 确定基底在各个数据点的取值向量basis
Mat = vander(basis); condition = cond(Mat);    % 用vander命令生成basis的范德蒙矩阵并求条件数
[L, U] = lu(Mat); vecx = (U\(L\vecy.')).'; vecx = fliplr(vecx);    % 标准lu分解解矩阵方程

% 生成句柄函数polyfunc
syms t;
monomial = (t - shift)/scale; vecsize = size(vecx, 2); funeval = vecx(vecsize);
for i = vecsize:-1:2    % 生成函数的算法采用Horner算法提高效率
    funeval = vecx(i - 1) + monomial*funeval;
end
polyfunc = matlabFunction(funeval, 'Vars', t);

end

　　比如对于点：$(-2,-27),(0,-1),(1,0)$ 它具有唯一的二次插值多项式：$p_2(t)=-1+5t-4t^2$ 。调用以上代码：

% 命令行输入
[polyfunc, vecx, condition] = MonoPI(vect, vecy)
% 命令行输出
polyfunc =
  包含以下值的 function_handle:
    @(t)-t.*(t.*4.0-5.0)-1.0
vecx =
    -1     5    -4
condition =
    6.0809

　　和预期完全一致。

2. 拉格朗日(Lagrange)插值

1）插值函数基

　　拉格朗日插值采用的是一种设计巧妙的多项式基，每个基底都是n-1次多项式，而每个基底函数当且仅当在第i个数据点处取1，在其余数据点均为零。这个多项式基是这样设计的：

$$l_j(t)=\frac{(t-t_1)(t-t_2)...(t-t_{j-1})(t-t_{j+1})...(t-t_n)}{(t_j-t_1)(t_j-t_2)...(t_j-t_{j-1})(t_j-t_{j+1})...(t_j-t_n)}=\frac{\prod\limits_{k=1,k\neq j}^n(t-t_k)}{\prod\limits_{k=1, k\neq j}^n(t_j-t_k)}$$　　因此就有：

$$l_j(t_i)=\delta_{ij}, i,j=1,2,...n $$　　其中，$\delta$ 为克罗内克(Kronecker)记号，当两个下标相等时为1，否则为零；也可以将 $\delta_{ij}$ 理解为一个二阶张量，即单位矩阵。只要将各个$t_i$ 带入定义式，上式是很容易验证的。这意味着拉格朗日插值的叠加系数的求解将会产生很好的性质，即：

2）叠加系数

　　需要求解的插值函数即：$f(t)=\sum\limits_{k=1}^nx_kl_k(t)$ ，而又已知：

$$l_1(t_1)x_1+l_2(t_1)x_2+...+l_n(t_1)x_n=y_1$$

$$l_1(t_2)x_1+l_2(t_2)x_2+...+l_n(t_2)x_n=y_2$$

$$... ... ... ... ...$$

$$l_1(t_n)x_1+l_2(t_n)x_2+...+l_n(t_n)x_n=y_n$$　　写成矩阵形式就是：

$$\begin{bmatrix}l_1(t_1)&l_2(t_1)&...&l_n(t_1)\\l_1(t_2)&l_2(t_2)&...&l_n(t_2)\\...&...&...&...\\l_1(t_n)&l_2(t_n)&...&l_n(t_n)\end{bmatrix} \begin{bmatrix}x_1\\x_2\\...\\x_n\end{bmatrix}=\begin{bmatrix}1&0&..&0\\0&1&..&0\\..&..&..&..\\0&0&..&1\end{bmatrix} \begin{bmatrix}x_1\\x_2\\...\\x_n\end{bmatrix}=I\boldsymbol{x}=\begin{bmatrix}x_1\\x_2\\...\\x_n\end{bmatrix}=\begin{bmatrix}y_1\\y_2\\...\\y_n\end{bmatrix}$$

　　其矩阵即单位矩阵，因此直接得出 $x_i=y_i$ ，$f(t)=p_{n-1}(t)=y_1l_1(t)+y_2l_2(t)+...+y_nl_n(t)=\sum\limits_{k=1}^ny_kl_k(t)$

3）问题条件和算法复杂度

　　拉格朗日插值生成的系数矩阵为单位矩阵，完全不存在条件病态的问题，只需要将各个数据点的取值作为系数即可。同样地，求解系数也将不存在任何复杂度。

　　但是，作为代价的是，函数求值开销较大。Horner嵌套算法可以用于单项式和牛顿插值表达式的求值，将总运算量大致控制在n次浮点数加法和n次浮点数乘法，但该算法不适用于拉格朗日插值的表达式。拉格朗日插值的求值的复杂度至少也要3n次浮点乘（除）法和2n次浮点加法以上，这还是在所有的系数（将插值系数和基底的分母合并以后的系数）都已经处理完成之后，而处理系数本身可能就需要 $n^2$ 级别的复杂度。此外，拉格朗日插值表达式也不利于求微分和积分；和牛顿插值相比，当新增数据点时不得不将所有的基底都改写，很不方便。总而言之，拉格朗日插值属于非常容易构造的一种插值，很适用于在理论上讨论某些问题，但在数值计算上仍具有很多劣势。

4）算法实现

　　实现拉格朗日多项式插值一种途径的MATLAB代码如下。此处的输出为多项式函数句柄。这些函数（句柄）只需要在函数名后面加括号变量即可调用，即polyfun(3)这样的形式。

function [ polyfun ] = LagrangePI( vect, vecy )
%   生成Lagrange插值多项式
%   输入两个参数：插值点行向量vect，函数行向量vecy；输出一个参数：插值多项式函数句柄polyfun
vecsize = size(vect, 2);
syms t f term;
f = 0;
for i = 1:vecsize
    term = vecy(i);
    for j = 1:vecsize
        if (j ~= i)
            term = term*(t - vect(j))/(vect(i) - vect(j));
        end
    end
    f = f + term;
end
polyfun = matlabFunction(f);
end

　　但是，由于多项式形式的函数表达式带入后为符号型变量，这意味着每一项的系数都经历了单独计算，每一项的分子也需要单独计算，这将使得拉格朗日插值表达式的函数求值(function evaluation)的复杂度达到 $O(n^2)$ 量级；如果想要使得每次求值能够控制在 $O(n)$ 量级，就必须实现计算出除了含有未知量的函数基分子以外的全部系数，同时在求值时也需要一些技巧。按照如下的书写方法可以实现这一目的：

function [ coefficients ] = newLagrangePI( vect, vecy )
%   生成Lagrange插值多项式的系数（计算分母）
%   输入两个参数：插值点行向量vect，函数行向量vecy；
%   输出一个参数：插值多项式的系数行向量coefficients；
vecsize = size(vect, 2);
coefficients = zeros(1, vecsize);
for i = 1:vecsize
    tmp = vecy(i);    % 取得基底函数对应的系数y_i
    for j = 1:vecsize    % 将其除以函数基底的分母
        if (j~=i)
            tmp = tmp/(vect(i) - vect(j));
        end
    end
    coefficients(i) = tmp;
end
end

　　除了求系数的函数还需要一个特别的求值函数：

function [ funeval ] = evaLagrangePI( coefficients, vect, vecy, t )
%   Lagrange插值多项式估值
%   输入四个参数：Lagrange插值的完整系数行向量coefficients，插值点行向量vect，函数行向量vecy，求值点t；
%   输出一个参数：函数在t处取值funeval
vecsize = size(vect, 2);
[found, index] = ismember(t, vect);
if found    % 如果求值点是原数据点，则直接返回原始信息中数据点的函数值
    funeval = vecy(index);
else    % 否则，先计算全部(t-t_i)的乘积
    funeval = 0; product = 1;
    for i = 1:vecsize
        product = product*(t - vect(i));
    end
    for i = 1:vecsize    % 然后，计算每一项的值，乘以该项的系数并且除以该项分子不存在的那项(t-t_i)
        funeval = funeval + coefficients(i)*product/(t - vect(i));
    end
end
end

　　同样是对于三点 $(-2,-27),(0,-1),(1,0)$ ，调用Lagrange插值方法：

vect = [-2, 0, 1]; vecy = [-27, -1, 0];
% 命令行输入
coefficients = newLagrangePI(vect, vecy)
% 命令行输出
coefficients =
   -4.5000    0.5000         0

% 命令行输入
val = evaLagrangePI(coefficients, vect, vecy, -2)
% 命令行输出
val =
   -27

% 命令行输入
val = evaLagrangePI(coefficients, vect, vecy, 0.5)
% 命令行输出
val =
    0.5000

　　所有的输出均和实际的多项式插值 $f(t)=p_2(t)=-1+5t-4t^2$ 吻合。

3. 牛顿(Newton)插值

1）插值函数基底

　　单项式基底非常简洁，缺点是求解方程组所用的是稠密的范德蒙矩阵，可能非常病态，复杂度也很高；拉格朗日基底比较精巧复杂，因为求解的系数矩阵是单位矩阵，求解很简单很准确，缺点是生成表达式和函数求值复杂度很高。牛顿插值方法在二者之间提供了一个折衷选项：基底不如拉格朗日的函数基那么复杂，而求解又比单项式基底大大简化，这来源于牛顿插值选取的基底：$$\pi_j(t)=\prod\limits_{k=1}^{j-1}(t-t_k)=(t-t_1)(t-t_2)...(t-t_{j-1}), j=1,...,n$$　　相对于拉格朗日基底的特殊性（$l_j(t_i)=\delta_{ij}$），牛顿插值基底具有一个弱一点的性质：$$\pi_j(t_i)=0,\forall i<j$$　　求出的多项式形如：$f(t)=p_{n-1}(t)=\sum\limits_{j=1}^nx_j\pi_j(t)=x_1+x_2(t-t_1)+...+x_n(t-t_1)(t-t_2)...(t-t_{n-1})$

2）叠加系数

$$\pi_1(t_1)x_1+\pi_2(t_1)x_2+...+\pi_n(t_1)x_n=y_1$$

$$\pi_1(t_2)x_1+\pi_2(t_2)x_2+...+\pi_n(t_2)x_n=y_2$$

$$............$$

$$\pi_1(t_n)x_1+\pi_2(t_n)x_2+...+\pi_n(t_n)x_n=y_n$$　　写成矩阵形式：

$$\begin{bmatrix}\pi_1(t_1)&\pi_2(t_1)&...&\pi_n(t_1)\\ \pi_1(t_2)&\pi_2(t_2)&...&\pi_n(t_2)\\...&...&...&...\\ \pi_1(t_n)&\pi_2(t_n)&...&\pi_n(t_n)\end{bmatrix} \begin{bmatrix}x_1\\x_2\\...\\x_n\end{bmatrix}=\begin{bmatrix}1&0&...&0\\1&t_2-t_1&...&0\\...&...&...&...\\1&t_n-t_1&...&(t_n-t_1)..(t_n-t_{n-1})\end{bmatrix}=\begin{bmatrix}y_1\\y_2\\...\\y_n\end{bmatrix}$$　　也就是说，牛顿插值的系数求解矩阵为一个下三角矩阵。

3）算法性质和算法复杂度

　　我们知道对于下三角矩阵，利用向前代入法可以比较便利地解出，其时间复杂度为 $O(n^2)$ 。再来看生成这个下三角矩阵，复杂度也是 $O(n^2)$ 的运算量。因此求解插值系数的总复杂度即 $O(n^2)$ 量级，比稠密矩阵的求解少一个量级。当然，求解牛顿插值系数不一定需要显示地生成矩阵，然后采用矩阵分解的标准套路；牛顿插值有好几种生成系数的方法可供选择，包括差商方法等，采用递归或者迭代都可以获得良好的效果，还能避免上溢出。

　　此外，牛顿插值的表达式在求值时适用Horner嵌套算法（太棒了！），这将把求值的复杂度控制在 $O(n)$ 的量级内，如果带上系数比拉格朗日插值表达式的求值要更高效。

牛顿插值方法有如下优越的性质：

3.1 当增加数据点时，可以仅仅通过添加一项函数基和增加一个系数，生成新的牛顿插值多项式。这其实是可以理解的，因为当新增点 $(t_{n+1},y_{n+1})$ 时，下三角系数矩阵所有的元素都没有发生任何变化，仅仅需要新增一列和一行即可，而在该矩阵右侧新增的一列全为零。这意味着所有的系数 $x_1,x_2,...x_n$ 不仅满足原线性方程组，也因此必定是新线性方程组解的部分。而基底部分也只是新增了一个基，所以新的插值多项式仅仅是老的插值多项式加一项而已，即 $f(t)^*=p_n(t)=p_{n-1}(t)+x_{n+1}\pi_{n+1}(t)$ 。对于新的这一项 $x_{n+1}\pi_{n+1}(t)$ 它的系数究竟如何取，只需要将新增的数据点带入即可求得：$$f(t_{n+1})^*=p_{n-1}(t_{n+1})+x_{n+1}\pi_{n+1}(t_{n+1})=y_{n+1}\quad \Rightarrow \quad x_{n+1}=\frac{y_{n+1}-p_{n-1}(t_{n+1})}{\pi_{n+1}(t_{n+1})}$$　　生成新系数的复杂度大致需要一次函数求值和一次基底求值，大致为 $O(n)$ 复杂度。如果迭代地使用这一公式，就可以生成全部牛顿插值多项式系数，复杂度 $O(n^2)$ ，和矩阵解法也大致是持平的。

3.2 差商法也可以实现生成牛顿插值多项式的系数。其中，差商 $f[]$ 的定义为：

$$f[t_1, t_2,...t_k]=\frac{f[t_2, t_3, ... t_{k}-f[t_1, t_2,...t_{k-1}]}{t_k-t_1}$$　　而牛顿多项式的系数则取自：$$x_j=f[t_1, t_2... t_j]$$　　对于这个可以有证明：

---

$$f[t_1]=y_1, x_1=y_1=f[t_1];\quad f[t_1, t_2]=\frac{f[t_2]-f[t_1]}{t_2-t_1}=\frac{y_2-y_1}{t_2-t_1},x_2=\frac{y_2-y_1}{t_2-t_1}=f[t_1, t_2]
$$
若$x_j=f[t_1, t_2, ...t_j]=\frac{f[t_2, t_3,...t_j]-f[t_1, t_2,...t_{j-1}]}{t_j-t_1}$ 对于任意 $j\leq k-1$ 成立，当 $j=k$ 时：

​ 考虑对于点 $(t_1, y_1), (t_2,y_2),...(t_{k-1},y_{k-1})$ 的 Newton 插值多项式 $p_1(t)$ ；对于点 $(t_2, y_2),(t_3, y_3),...$$(t_k, y_k)$ 的 Newton 插值多项式 $p_2(t)$ ，并且已知分差插值系数对任意 $j\leq k-1$ 均成立，因而有：
$$
p_1(t)=\sum\limits_{j=1}^{k-1}a_j\pi_j(t), \quad p_2(t)=\sum\limits_{j=2}^{k}b_j\pi_j(t),\qquad a_j=f[t_1,...t_{j}],b_j=f[t_2,...t_j]
$$
由 $p_1(t)$ 过点 $(t_1, y_1)$ 到 $(t_{k-1},y_{k-1})$ ，$p_2(t)$ 过点 $(t_2,y_2)$ 到 $(t_k,y_k)$ ，构造插值多项式：
$$
p(t)=\frac{t_k-t}{t_k-t_1}p_1(t)+\frac{t-t_1}{t_k-t_1}p_2(t)
$$
就有该多项式通过点 $(t_1, y_1)$ 到 $(t_k,y_k)$ ，因此即为所求的 Newton 插值多项式。带入 $p_1(t),p_2(t)$ 表达式，并比较等式两端最高次项系数即得：
$$
p(t)=\sum\limits_{j=1}^kx_j\pi_j(t)=\frac{t_k-t}{t_k-t_1}\sum\limits_{j=1}^{k-1}a_j\pi_j(t)+\frac{t-t_1}{t_k-t_1}\sum\limits_{j=2}^{k}b_j\pi_j'(t)\\
x_k=\frac{-1}{t_k-t_1}a_{k-1}+\frac{1}{t_k-t_1}b_k=\frac{f[t_2,...t_k]-f[t_1,...t_{k-1}]}{t_k-t_1}=f[t_1, ...t_k]\qquad \square
$$

---

这个证明我摘录自奥斯陆大学数学系的 Michael S. Floater 在 Newton Interpolation 讲义里面写的证明。

4）算法实现

　　根据3.1，可以通过新增节点的方法迭代地生成插值系数。利用这种思路的实现代码如下：

function [ vecx_new, vect_new ] = newNPI( vect, vecx, newPoint )
%	Newton插值算法新增节点函数；
%   输入三个参数：原插值点行向量vect，原插值系数行向量vecx，新增节点newPoint；
%   输入两个参数：新系数行向量vecx_new，新插值点行向量vect_new；
vecsize = size(vecx, 2);
vecx_new = zeros(1, vecsize + 1); vecx_new(1:vecsize) = vecx;
vect_new = zeros(1, vecsize + 1); vect_new(1:vecsize) = vect; vect_new(vecsize + 1) = newPoint(1);
p_new = HornerNPI(vect, vecx, newPoint(1)); w_new = 1;
for i = 1:vecsize
    w_new = w_new * (newPoint(1) - vect(i));
end
vecx_new(vecsize + 1) = (newPoint(2) - p_new) / w_new;
end

　　新增节点函数newNPI可以单独使用；同时也可以反复调用生成牛顿插值系数，如下：

function [ polyfun, vecx ] = newNewtonPI( cvect, cvecy )
%    使用新增节点函数逐渐更新产生Newton插值多项式系数；
%    输入两个参数：插值点行向量cvect，插值系数行向量cvecx；
%    输出两个参数：多项式函数句柄polyfun，系数行向量vecx；

%    迭代生成系数行向量
vect = cvect(1); vecx = cvecy(1);
vecsize = size(cvect, 2);
for i=2:vecsize
    [vecx, vect] = newNPI(vect, vecx, [cvect(i), cvecy(i)]);
end

%    采用Horner嵌套算法生成多项式函数句柄
syms f t; f = vecx(vecsize);
for i = vecsize-1:-1:1
    f = vecx(i) + (t - cvect(i)) * f;
end
polyfun = matlabFunction(f);
end

　　另一种方法是采用差商。以下是实现的代码。和之前的说法不同的是，本代码使用的并非递归，而是正向的类似函数值缓存的算法。

function [ polyfun, vecx ] = recNewtonPI( vect, vecy )
%    使用差商产生Newton插值多项式系数；
%    输入两个参数：插值点行向量vect，函数取值cvecy；
%    输出两个参数：多项式函数polyfun，系数行向量vecx；
vecsize = size(vect, 2);
Div = diag(vecy);

% 差商生成系数行向量vecx
for k = 1:vecsize-1
    for i = 1:vecsize-k
        Div(i, i+k) = (Div(i+1, i+k) - Div(i, i+k-1))/(vect(i+k) - vect(i));
    end
end
vecx = Div(1, :);

% 生成多项式函数polyfun
syms f t; f = vecx(vecsize);
for i = vecsize-1:-1:1
    f = vecx(i) + (t - vect(i)) * f;
end
polyfun = matlabFunction(f);
end

　　但不论如何，产生的结果完全一致。用同样的例子：

vect=[-2, 0, 1]; vecy=[-27, -1, 0];

% 命令行输入1，调用新增节点方法
[polyfun, vecx] = newNewtonPI(vect, vecy)

% 命令行输入2，调用差商方法
[polyfun, vecx] = recNewtonPI(vect, vecy)

% 命令行输出1/2，完全相同
polyfun =
  包含以下值的 function_handle:
    @(t)-(t.*4.0-1.3e1).*(t+2.0)-2.7e1
vecx =
   -27    13    -4

　　容易检验，该多项式函数正是原数据点的多项式插值函数。