Luogu 4281 [AHOI2008]紧急集合 / 聚会

BZOJ 1832

写起来很放松的题。

首先发现三个点在树上一共只有$3$种形态，大概长这样：

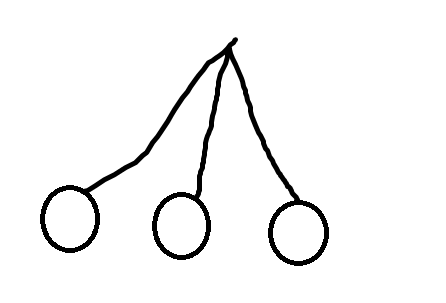
这种情况下显然走到三个点的$lca$最优。

这种情况下走到中间那个点最优。

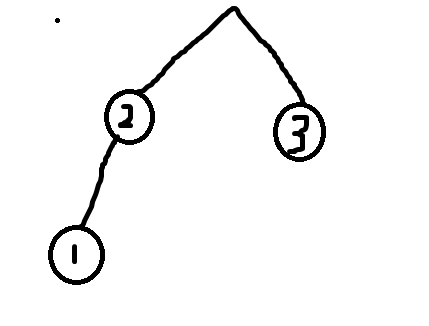
这种情况下走到$2$最优。

有趣的事情来了：我们发现树上的三个点，会有三个$lca$，而当两个$lca$相同时，另外一个$lca$就成了最优解。

考虑一下怎么计算路程，只要分别算算三个图就会发现最后路程的式子也是统一的，（假设点为$x, y, z$）就是$dep_x + dep_y + dep_z - dep_{lca(x, y)} - dep_{lca(y, z)} - dep_{lca(x, z)}$。

时间复杂度$O(nlogn)$。

感觉倍增挺卡的，但是$2 * n = 1e6$完全不敢$rmq$啊$233$，链剖应该是比较优秀的做法吧。

Code：

#include <cstdio>
#include <cstring>
using namespace std;

const int N = 5e5 + ;
const int Lg = ;

int n, qn, tot = , head[N], dep[N], fa[N][Lg];

struct Edge {
    int to, nxt;
} e[N << ];

inline void add(int from, int to) {
    e[++tot].to = to;
    e[tot].nxt = head[from];
    head[from] = tot;
}

inline void swap(int &x, int &y) {
    int t = x; x = y; y = t;
}

inline void read(int &X) {
    X = ; char ch = ; int op = ;
    for(; ch > ''|| ch < ''; ch = getchar())
        if(ch == '-') op = -;
    for(; ch >= '' && ch <= ''; ch = getchar())
        X = (X << ) + (X << ) + ch - ;
    X *= op;
}

void dfs(int x, int fat, int depth) {
    fa[x][] = fat, dep[x] = depth;
    for(int i = ; i <= ; i++)
        fa[x][i] = fa[fa[x][i - ]][i - ];
    for(int i = head[x]; i; i = e[i].nxt) {
        int y = e[i].to;
        if(y == fat) continue;
        dfs(y, x, depth + );
    }
}

inline int getLca(int x, int y) {
    if(dep[x] < dep[y]) swap(x, y);
    for(int i = ; i >= ; i--)
        if(dep[fa[x][i]] >= dep[y])
            x = fa[x][i];
    if(x == y) return x;
    for(int i = ; i >= ; i--)
        if(fa[x][i] != fa[y][i])
            x = fa[x][i], y = fa[y][i];
    return fa[x][];
}

int main()  {
    read(n), read(qn);
    for(int x, y, i = ; i < n; i++) {
        read(x), read(y);
        add(x, y), add(y, x);
    }
    dfs(, , );

    for(int x, y, z; qn--; ) {
        read(x), read(y), read(z);
        int xy = getLca(x, y), yz = getLca(y, z), xz = getLca(x, z), res;
        if(xy == yz) res = xz;
        else if(xy == xz) res = yz;
        else if(yz == xz) res = xy;
        printf("%d %d\n", res, dep[x] + dep[y] + dep[z] - dep[xy] - dep[yz] - dep[xz]);
    }

    return ;
}