P4219 [BJOI2014]大融合 LCT维护子树大小

\(\color{#0066ff}{ 题目描述 }\)

小强要在\(N\)个孤立的星球上建立起一套通信系统。这套通信系统就是连接\(N\)个点的一个树。 这个树的边是一条一条添加上去的。在某个时刻，一条边的负载就是它所在的当前能够 联通的树上路过它的简单路径的数量。

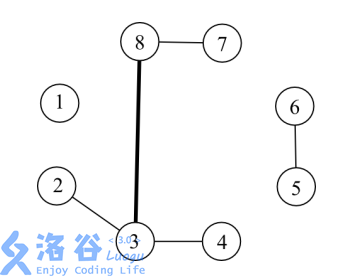
例如，在上图中，现在一共有了\(5\)条边。其中，\((3,8)\)这条边的负载是\(6\)，因 为有六条简单路径\(2-3-8\)，\(2-3-8-7\)，\(3-8\)，\(3-8-7\)，\(4-3-8\)，\(4-3-8-7\)路过了\((3,8)\)。

现在，你的任务就是随着边的添加，动态的回答小强对于某些边的负载的 询问。

\(\color{#0066ff}{输入格式}\)

第一行包含两个整数 \(N, Q\),表示星球的数量和操作的数量。星球从 \(1\) 开始编号。

接下来的 \(Q\) 行，每行是如下两种格式之一：

• A x y 表示在 \(x\)和 \(y\) 之间连一条边。保证之前 \(x\) 和 \(y\)是不联通的。
• Q x y表示询问 \((x,y)\) 这条边上的负载。保证 \(x\) 和 \(y\) 之间有一条边。

\(\color{#0066ff}{输出格式}\)

对每个查询操作，输出被查询的边的负载。

\(\color{#0066ff}{输入样例}\)

8 6
A 2 3
A 3 4
A 3 8
A 8 7
A 6 5
Q 3 8

\(\color{#0066ff}{输出样例}\)

6

\(\color{#0066ff}{数据范围与提示}\)

对于所有数据，\(1≤N,Q≤10^5\)

\(\color{#0066ff}{ 题解 }\)

众所周知，LCT是维护树链的强力数据结构

对于维护一个子树的信息，是不太好维护的

但是动态的连边删边又不得不用LCT

其实，LCT维护一个子树信息并没有那么难

显然本题要维护的是子树siz

我们记tot为子树大小，siz为虚子树大小之和（LCT虚实边）

我们考虑LCT的哪些函数会影响这些东西

首先，upd肯定是要改的，即

void upd() {
	tot = siz + 1;
	if(ch[0]) tot += ch[0]->tot;
	if(ch[1]) tot += ch[1]->tot;
}

注意，左右孩子实际上是splay维护的一条链上的两个点

tot初始为自己的虚子树的和+自己大小1

如果有实儿子，统计总共的大小

接下来rot和splay，显然不会改变边的虚实，所以直接维护即可

然后是access，它会改变很多边的虚实，所以会产生影响

也好维护，让x的siz减掉即将变成实边的虚边的贡献，加上即将变为虚边的实边的贡献即可

makeroot， findroot都没有影响qwq

link，有影响， 因为连了一条虚边，只需加一下贡献即可，加完后upd一下

注意link的不光要makeroot(x)，还要把y弄到根上去，这样y就没有祖先了，再加就不会影响了

#include<bits/stdc++.h>
#define LL long long
LL in() {
	char ch; LL x = 0, f = 1;
	while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
	return x * f;
}
const int maxn = 1e5 + 100;
struct LCT {
protected:
	struct node {
		node *ch[2], *fa;
		int siz, rev, tot;
		node(int siz = 0, int rev = 0, int tot = 1): siz(siz), rev(rev), tot(tot) { ch[0] = ch[1] = fa = NULL; }
		void trn() { std::swap(ch[0], ch[1]), rev ^= 1; }
		void dwn() {
			if(!rev) return;
			if(ch[0]) ch[0]->trn();
			if(ch[1]) ch[1]->trn();
			rev = 0;
		}
		void upd() {
			tot = siz + 1;
			if(ch[0]) tot += ch[0]->tot;
			if(ch[1]) tot += ch[1]->tot;
		}
		bool isr() { return fa->ch[1] == this; }
		bool ntr() { return fa && (fa->ch[0] == this || fa->ch[1] == this); }
	}pool[maxn];
	void rot(node *x) {
		node *y = x->fa, *z = y->fa;
		bool k = x->isr(); node *w = x->ch[!k];
		if(y->ntr()) z->ch[y->isr()] = x;
		(x->ch[!k] = y)->ch[k] = w;
		(y->fa = x)->fa = z;
		if(w) w->fa = y;
		y->upd(), x->upd();
	}
	void splay(node *o) {
		static node *st[maxn];
		int top;
		st[top = 1] = o;
		while(st[top]->ntr()) st[top + 1] = st[top]->fa, top++;
		while(top) st[top--]->dwn();
		while(o->ntr()) {
			if(o->fa->ntr()) rot(o->isr() ^ o->fa->isr()? o : o->fa);
			rot(o);
		}
	}
	void access(node *x) {
		for(node *y = NULL; x; x = (y = x)->fa) {
			splay(x);
			if(x->ch[1]) x->siz += x->ch[1]->tot;
			x->ch[1] = y;
			if(y) x->siz -= y->tot;
			x->upd();
		}
	}
	void makeroot(node *o) { access(o), splay(o), o->trn(); }
public:
	void link(int l, int r) {
		node *x = pool + l, *y = pool + r;
		makeroot(x), access(y), splay(y);
		(x->fa = y)->siz += x->tot;
		y->upd();
	}
	int query(int l, int r) {
		node *x = pool + l, *y = pool + r;
		makeroot(x), access(y), splay(y);
		return (x->siz + 1) * (y->siz + 1);
	}
}s;
int n, m;
char getch() {
	char ch;
	while(!isalpha(ch = getchar()));
	return ch;
}
int main() {
	n = in(), m = in();
	for(int i = 1; i <= m; i++) {
		if(getch() == 'A') s.link(in(), in());
		else printf("%d\n", s.query(in(), in()));
	}
	return 0;
}