CF24D Broken robot 后效性DP

这题咕了好久.....

---

设$f[i][j]$表示从$(i,j)$到最后一行的期望步数；

则有

$ f[i][1]=\frac{1}{3}(f[i][1]+f[i][2]+f[i+1][1])+1$

$ f[i][m]=\frac{1}{3}(f[i][m]+f[i][m-1]+f[i+1][m])+1$

$ f[i][j]=\frac{1}{4}(f[i][j]+f[i][j-1]+f[i][j+1]+f[i+1][j])+1$

所以他有后效性（于是我们疯狂迭代）

然而要高斯消元。。。。

具体的来说，就是把每行的每个转移都写在系数矩阵里，对这一行进行高斯消元；增广矩阵要写已知量；

化简上面的式子：

$\frac{2}{3}*f[i][1]-\frac{1}{3}*f[i][2]=\frac{1}{3}*f[i+1][1]+1 $

$\frac{2}{3}*f[i][m]-\frac{1}{3}*f[i][m-1]=\frac{1}{3}*f[i+1][m]+1$

$\frac{3}{4}*f[i][j]-\frac{1}{4}*f[i][j-1]-\frac{1}{4}*f[i][j+1]=\frac{1}{4}*f[i+1][j]+1$

注意，高斯消元消的是某一行，每个位置的值。

又注意到上面的有分数不美观，实际写的时候可以化简（方程两边同乘1个数）。

还有，高斯消元的过程需要简化

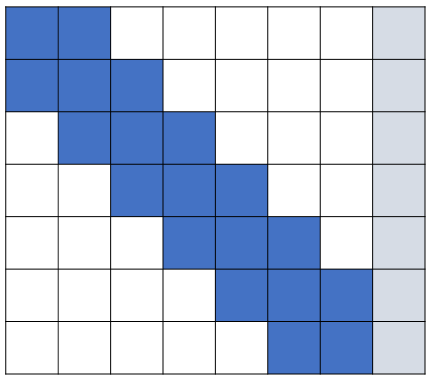
深蓝代表系数矩阵中有数的位置，浅灰蓝色为增广矩阵。

先消成这个样子：

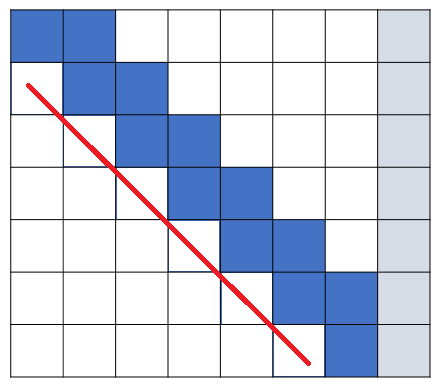
然后从最后一行向上代入

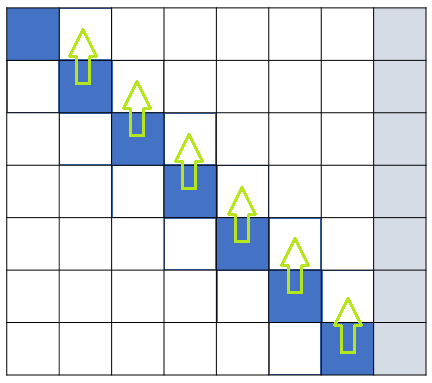
#include<cstdio>
#include<iostream>
#define R register int
#define db double
using namespace std;
inline int g() {
    R ret=,fix=; register char ch; while(!isdigit(ch=getchar())) fix=ch=='-'?-:fix;
    do ret=ret*+(ch^); while(isdigit(ch=getchar())); return ret*fix;
}
int n,m,x,y;
db f[],a[][];
inline void init() {
    a[][]=,a[][]=-,a[][m+]=+f[];
    a[m][m]=,a[m][m-]=-,a[m][m+]=+f[m];
    for(R i=;i<m;++i) a[i][i]=,a[i][i-]=a[i][i+]=-,a[i][m+]=f[i]+;
}
inline void Gauss() {
    for(R i=;i<=m;++i) { if(i<m) a[i][i+]/=a[i][i];
        a[i][m+]/=a[i][i],a[i][i]=;
        a[i+][i+]-=a[i][i+]*a[i+][i];
        a[i+][m+]-=a[i][m+]*a[i+][i],a[i+][i]=;
    } for(R i=m-;i;--i) a[i][m+]-=a[i][i+]*a[i+][m+];
    for(R i=;i<=m;++i) f[i]=a[i][m+];
}
signed main() {
    n=g(),m=g(),x=g(),y=g();
    if(m==) printf("%.10lf\n",(db)*(n-x));
    else { for(R i=n-;i>=x;--i) {
            init(); Gauss();
        } printf("%.10lf\n",f[y]);
    }
} 

---

2019.05.24