算法金 | 再见，PCA 主成分分析！

​大侠幸会，在下全网同名[算法金] 0 基础转 AI 上岸，多个算法赛 Top [日更万日，让更多人享受智能乐趣]

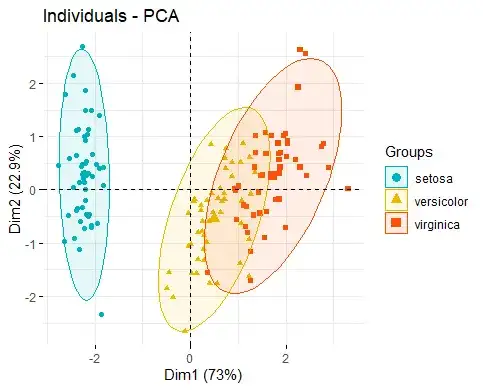
1. 概念：数据降维的数学方法

定义

• 主成分分析（PCA）是一种统计方法，通过正交变换将一组可能相关的变量转换为一组线性不相关的变量，这组新的变量称为主成分。
• 大白话，PCA能够从数据中提取出最重要的特征，通过减少变量的数量来简化模型，同时保留原始数据集中的大部分信息。

特点

• PCA是最广泛使用的数据降维技术之一，能够有效地揭示数据的内部结构，减少分析问题的复杂度。

应用领域

• 图像处理：图像压缩和特征提取。
• 金融数据分析：风险管理、股票市场分析。
• 生物信息学：基因数据分析、疾病预测。
• 社会科学研究：问卷数据分析、人口研究。

2 核心原理：方差最大化

• 方差最大化：
• PCA通过找到数据方差最大的方向来确定主成分，然后找到次大方向，且这些方向必须是相互正交的。
• 这样做的目的是保证降维后的数据能够保留最多的原始数据信息。

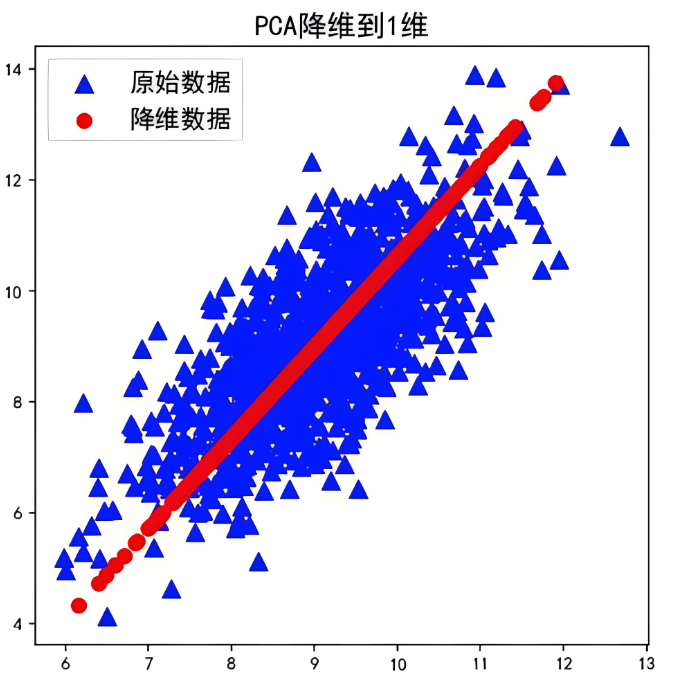
• 计算步骤：

1. 数据标准化：使得每个特征的平均值为0，方差为1。
2. 计算协方差矩阵：反映变量之间的相关性。
3. 计算协方差矩阵的特征值和特征向量：特征向量决定了PCA的方向，特征值决定了方向的重要性。
4. 选择主成分：根据特征值的大小，选择最重要的几个特征向量，构成新的特征空间。

3 优缺点分析

• 优点：
• 降维效果显著：能够有效地减少数据的维度，同时尽可能地保留原始数据的信息。
• 揭示数据结构：有助于发现数据中的模式和结构，便于进一步分析。
• 无需标签数据：PCA是一种无监督学习算法，不需要数据标签。
• 缺点：
• 线性限制：PCA只能捕捉到数据的线性关系和结构，对于非线性结构无能为力。
• 方差并非信息量的唯一衡量：有时候数据的重要性并不仅仅体现在方差上，PCA可能会忽略掉一些重要信息。
• 对异常值敏感：异常值可能会对PCA的结果产生较大影响。

4 PCA 实战

介绍一个用于主成分分析的 Python 库

PCA的核心是构建在sklearn功能之上，以便在与其他包结合时实现最大的兼容性。

除了常规的PCA外，它还可以执行SparsePCA和TruncatedSVD。

其他功能包括：

• 使用Biplot绘制载荷图
• 确定解释的方差
• 提取性能最佳的特征
• 使用载荷绘制的散点图
• 使用Hotelling T2和/或SPE/Dmodx进行异常值检测

pip install pca

from pca import pca  # 导入PCA模块
import numpy as np
import pandas as pd
# Dataset
from sklearn.datasets import load_iris  # 导入鸢尾花数据集
# 从鸢尾花数据集中创建DataFrame对象
X = pd.DataFrame(data=load_iris().data, columns=load_iris().feature_names, index=load_iris().target)
# 初始化PCA模型，指定主成分数量为3，并进行数据标准化
model = pca(n_components=3, normalize=True)
# 拟合并转换数据
out = model.fit_transform(X)
# 创建只包含方向的图
fig, ax = model.biplot(textlabel=True, legend=False, figsize=(10, 6))

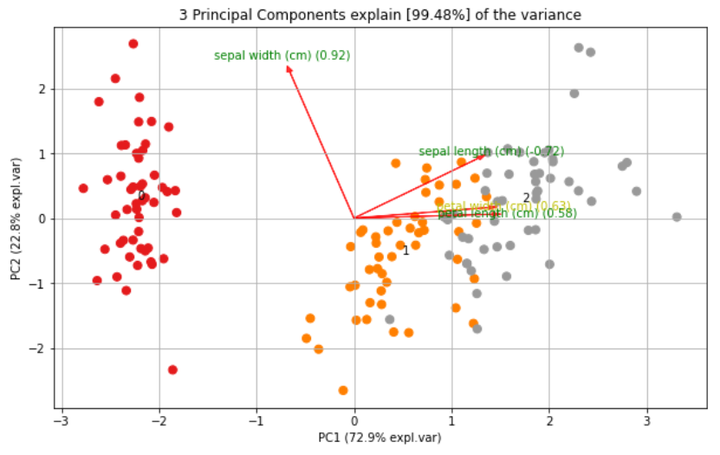
下面我们使用 sklearn 里面的 PCA 工具，在一组人脸数据上直观感受下，

# 导入必要的库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_olivetti_faces
from sklearn.decomposition import PCA
# 加载Olivetti人脸数据集
faces_data = fetch_olivetti_faces()
X = faces_data.data
# 可视化原始图像和对应的主成分
n_images = 4  # 每行显示的图像数量
n_rows = 4    # 总共的行数
fig, axes = plt.subplots(n_rows, 2*n_images, figsize=(16, 10), subplot_kw={'xticks':[], 'yticks':[]})
# 使用PCA降维
n_components = 50  # 设置PCA保留的主成分数量
pca = PCA(n_components=n_components, whiten=True, random_state=42)
X_pca = pca.fit_transform(X)
for r in range(n_rows):
    for i in range(n_images):
        index = r * n_images + i
        axes[r, 2*i].imshow(X[index].reshape(64, 64), cmap='gray')
        axes[r, 2*i].set_title(f'大侠 {index+1} 图像', fontproperties='SimHei')  # 手动设置字体
        axes[r, 2*i+1].imshow(pca.inverse_transform(X_pca[index]).reshape(64, 64), cmap='bone')
        axes[r, 2*i+1].set_title(f'大侠 {index+1} 主成分', fontproperties='SimHei')  # 手动设置字体
plt.tight_layout()
plt.show()

我们保留了前 50 个主成分

通过可视化对比图直观感受下，信息保留了多多少，损失了多少

通过对比图可以看到，某一张人脸的基本信息都保留了下来

如果保留 前 100 个主成分，那就更接近原始图片了

你也可以试下，保留 1 个主成分会怎样？通过保留的信息你还认得出来哪过大侠是哪过吗

[ 算法金，碎碎念 ]

• 最近 【不上班】 这个词频繁出现在朋友圈，貌似很火
• 不上班，站着把钱赚了，大概率不可能的
• 不上班，躺着把钱赚了（别想歪了），更是绝大概率不可能的
• 有些圈子，天然就是靠博眼球来筛选用户，真的很可怕
• 想到了一句话【当大家都有病时，你就不觉得这是病了】
• 在这种圈子呆久了，大概率会沦陷的，别以外自己不会，咱都是普通人
• 大部分人都是普通人，普通人通常都不信概率，而概率恰恰是反映常态 分布的
• 悲剧，卒~

全网同名，日更万日，让更多人享受智能乐趣

烦请大侠多多 分享、在看、点赞，助力算法金又猛又持久、很黄很 BL 的日更下去；我们一起，让更多人享受智能乐趣

同时邀请大侠 关注、星标 算法金，围观日更万日，助你功力大增、笑傲江湖