8.16考试总结(NOIP模拟41)[你相信引力吗·marshland·party?·半夜]
美丽的不是这个世界,而是看世界的你的眼神。
T1 你相信引力吗
解题思路
好像只有我一个人没有看出来这个题是单调栈(现在一看区间问题就是双指针,线段树)
维护一个单调递减的栈。
我们把最大值放到左端点,这样可以使一个弧不在一起的情况更加好处理。
对于当前扫到的点,一定可以和栈里小于等于这个数的点连边,还可以和大于这个数的第一个点连边。
对于相等的数,维护一下个数就好了。
然后对于最后扫完之后栈里剩下的元素,都一定是可以和最大值连边的,直接计算就好了
code
#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define f() cout<<"Pass"<<endl
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=5e6+10;
int n,id,ans,s[N<<1],sum[N];
struct Stack
{
int all,num[N];
bool empty(){return all==0;}
int top(){return num[all];}
void push(int x){num[++all]=x;}
void pop(){all--;}
};
Stack sta;
signed main()
{
n=read();
for(int i=1;i<=n;i++) s[i+n]=s[i]=read()+1;
for(int i=1;i<=n;i++) if(s[i]>s[id]) id=i;
for(int i=id;i<=id+n-1;i++)
{
while(!sta.empty()&&sta.top()<s[i]){ans++;sta.pop();}
ans+=(sta.top()>s[i])?1:sum[sta.all]+(s[id]!=s[i]);
sum[sta.all+1]=(sta.top()==s[i])?sum[sta.all]+1:1;
sta.push(s[i]);
}
while(sta.all>2&&sta.num[2]!=sta.top()) ans++,sta.pop();
printf("%lld",ans);
return 0;
}
T2 marshland
解题思路
果然网络流题目最大的特点就是看不出来是网络流。
本题就是最大费用可行流,把每个有危险的点拆成两个。
建图的话有四列点:
没有危险值,并且横坐标是奇数的
有危险值的入点
有危险值的出点
没有危险值,并且横坐标是偶数的
边的容量都是 1 ,除了有危险值的点自己和自己之间费用是 自身危险值 之外,其它的全部是 0 。
建图原因:因为要保证每一次只放置一个石头,因此容量为 1 。
由于 L 形状的石头放在没有危险值的部分一定是相邻的两行,一奇一偶,因此没危险值的分为两列建边。
不一定要放置 m 个,所以每跑一次就更新一次答案就好了。
code
#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define f() cout<<"Pass"<<endl
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=5e3+10,M=5e5+10;
int n,m,K,fro,t,ans,sum,dis[N],flow[N],pre[N],las[N],s[60][60],mincost;
int tot=1,head[N],nxt[M<<1],ver[M<<1],edge[M<<1],val[M<<1];
int d1[6]={0,1,0,0,-1};
int d2[6]={0,0,-1,1,0};
bool vis[N];
struct Queue
{
int l,r,num[M];
void clear(){l=1;r=0;}
void push(int x){num[++r]=x;}
void pop(){l++;}
int front(){return num[l];}
bool empty(){return l>r;}
};
Queue q;
void add_edge(int x,int y,int ed,int va)
{
ver[++tot]=y;
edge[tot]=ed;
val[tot]=va;
nxt[tot]=head[x];
head[x]=tot;
}
void add(int x,int y,int va)
{
add_edge(x,y,1,va);
add_edge(y,x,0,-va);
}
bool SPFA()
{
memset(dis,-0x3f,sizeof(dis));
memset(flow,0x3f,sizeof(flow));
q.clear();
q.push(fro);
dis[fro]=0; vis[fro]=true;
pre[t]=-1;
while(!q.empty())
{
int x=q.front();
vis[x]=false; q.pop();
for(int i=head[x];i;i=nxt[i])
{
int to=ver[i];
if(edge[i]>0&&dis[to]<dis[x]+val[i])
{
dis[to]=dis[x]+val[i];
flow[to]=min(flow[x],edge[i]);
pre[to]=x; las[to]=i;
if(!vis[to]) q.push(to),vis[to]=true;
}
}
}
return pre[t]!=-1;
}
void MCMF()
{
int all=1;
while(all<=m&&SPFA())
{
int x=t; all++;
mincost+=flow[t]*dis[t];
ans=max(ans,mincost);
while(x!=fro)
{
edge[las[x]]-=flow[t];
edge[las[x]^1]+=flow[t];
x=pre[x];
}
}
}
signed main()
{
n=read(); m=read(); K=read();
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
s[i][j]=read();
sum+=s[i][j];
}
for(int i=1,x,y;i<=K;i++)
{
x=read(); y=read();
s[x][y]=-1;
}
fro=2*n*n+1; t=2*n*n+2;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if((i+j)&1)
{
if(s[i][j]==-1) continue;
add((i-1)*n+j,n*n+(i-1)*n+j,s[i][j]);
for(int k=1;k<=4;k++)
{
int x=i+d1[k],y=j+d2[k];
if(x<=0||y<=0||x>n||y>n) continue;
if(s[x][y]==-1) continue;
if(x&1) add((x-1)*n+y,(i-1)*n+j,0);
else add(n*n+(i-1)*n+j,n*n+(x-1)*n+y,0);
}
}
else
{
if(s[i][j]==-1) continue;
if(i&1) add(fro,(i-1)*n+j,0);
else add(n*n+(i-1)*n+j,t,0);
}
MCMF();
printf("%lld",sum-ans);
return 0;
}
T3 party?
解题思路
暴力跳的话有 86 pts的巨额分数。(TLE的点是链)
主要是一个 Hall定理。
对于一个二分图 \(X\),\(Y\),并且\(|X|=|Y|\),设点集 \(S\) 向另一侧的连边并集为 \(M(S)\) ,那么对于 \(X\) 的任何子集都有 \(|S|\le|M(S)|\),这是满足二分图存在完美匹配的充要条件。
不难发现其实人就是 X,Y 就是特产,并且一定满足上述条件。
因此对于每一个询问我们只需要枚举人们的各种组合方案,然后对于答案取个 min 。
接下来考虑如何快速求出每个人所可以携带的特产。
不难发现其实每个城市的连边就构成了一棵类似于树的结构。
因此可以用树剖+线段树维护一个 bitset 。
code
86pts暴力
#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define f() cout<<"Pass"<<endl
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=3e5+10,M=5e4+10,INF=1e18;
int n,m,qus,p[N],s[N],res[6];
bitset<1010> bit[10],all;
bool flag1,flag2;
struct Ques
{
int c,dat[6];
}q[M];
bool check(int x,int cnt,int ov)
{
for(int i=1;i<=cnt;i++)
if(res[i]<x)
ov-=x-res[i];
return ov>=0;
}
signed main()
{
n=read(); m=read(); qus=read();
if(!qus) return 0;
for(int i=2;i<=n;i++)
{
p[i]=read();
if(p[i]!=i-1) flag2=true;
}
for(int i=1;i<=n;i++)
s[i]=read();
for(int i=1;i<=qus;i++)
{
q[i].c=read();
if(q[i].c!=2) flag1=true;
for(int j=1;j<=q[i].c;j++)
q[i].dat[j]=read();
}
for(int i=1;i<=qus;i++)
{
int cnt=q[i].c,minn=INF,ans=m;
for(int j=1;j<=cnt;j++)
bit[j].reset();
for(int j=1;j<=cnt;j++)
minn=min(minn,q[i].dat[j]);
while(1)
{
for(int j=1;j<=cnt;j++)
while(q[i].dat[j]>minn)
{
bit[j][s[q[i].dat[j]]]=true;
q[i].dat[j]=p[q[i].dat[j]];
}
int pre=minn;
for(int j=1;j<=cnt;j++)
minn=min(minn,q[i].dat[j]);
if(pre==minn) break;
}
for(int j=1;j<=cnt;j++)
while(q[i].dat[j]>minn)
{
bit[j][s[q[i].dat[j]]]=true;
q[i].dat[j]=p[q[i].dat[j]];
}
for(int j=1;j<=cnt;j++)
bit[j][s[q[i].dat[j]]]=true;
for(int sta=1;sta<(1<<cnt);sta++)
{
int sum=0; all.reset();
for(int j=1;j<=cnt;j++)
if((sta>>j-1)&1)
all|=bit[j],sum++;
ans=min(ans,(int)all.count()/sum);
}
printf("%lld\n",ans*cnt);
}
return 0;
}
正解
#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define f() cout<<"Pass"<<endl
#define ls x<<1
#define rs x<<1|1
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=3e5+10,M=1e3+10,INF=1e18;
int n,m,q,cnt,pos[6],s[N];
int tim,dfn[N],id[N],siz[N],fa[N],topp[N],son[N],dep[N];
int tot=1,head[N],ver[N<<1],nxt[N<<1];
bitset<M> tre[N<<2],pre[N],all,bit[6];
void add_edge(int x,int y)
{
ver[++tot]=y;
nxt[tot]=head[x];
head[x]=tot;
}
void dfs1(int x)
{
siz[x]=1;
for(int i=head[x];i;i=nxt[i])
{
int to=ver[i];
dep[to]=dep[x]+1;
fa[to]=x;
dfs1(to);
siz[x]+=siz[to];
if(siz[to]>siz[son[x]])
son[x]=to;
}
}
void dfs2(int x,int tp)
{
dfn[x]=++tim;
id[tim]=x;
topp[x]=tp;
if(son[x]) dfs2(son[x],tp);
for(int i=head[x];i;i=nxt[i])
if(!dfn[ver[i]])
dfs2(ver[i],ver[i]);
}
int LCA(int x,int y)
{
if(!x||!y) return 0;
while(topp[x]^topp[y])
{
if(dep[topp[x]]<dep[topp[y]])
swap(x,y);
x=fa[topp[x]];
}
if(dep[x]>dep[y])
swap(x,y);
return x;
}
void dfs3(int x)
{
if(topp[x]==x) pre[x][s[x]]=true;
else pre[x]=pre[fa[x]],pre[x][s[x]]=true;
for(int i=head[x];i;i=nxt[i])
dfs3(ver[i]);
}
void push_up(int x)
{
tre[x]=tre[ls]|tre[rs];
}
void build(int x,int l,int r)
{
if(l==r)
{
tre[x][s[id[l]]]=true;
return ;
}
int mid=(l+r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
push_up(x);
}
bitset<M> query(int x,int l,int r,int L,int R)
{
if(L<=l&&r<=R) return tre[x];
int mid=(l+r)>>1;
bitset<M> temp; temp.reset();
if(L<=mid) temp=query(ls,l,mid,L,R);
if(R>mid) temp|=query(rs,mid+1,r,L,R);
return temp;
}
bitset<M> query(int x,int y)
{
bitset<M> temp; temp.reset();
while(topp[x]^topp[y])
{
temp|=pre[x];
x=fa[topp[x]];
}
temp|=query(1,1,tim,dfn[y],dfn[x]);
return temp;
}
signed main()
{
n=read(); m=read(); q=read();
for(int i=2,x;i<=n;i++)
x=read(),add_edge(x,i);
for(int i=1;i<=n;i++)
s[i]=read();
dfs1(1); dfs2(1,1);
dfs3(1); build(1,1,tim);
while(q--)
{
cnt=read();
for(int i=1;i<=cnt;i++)
pos[i]=read();
int lca=pos[1],ans=m;
for(int i=1;i<=cnt;i++)
lca=LCA(lca,pos[i]);
for(int i=1;i<=cnt;i++)
bit[i]=query(pos[i],lca);
for(int sta=1;sta<(1<<cnt);sta++)
{
int sum=0; all.reset();
for(int i=1;i<=cnt;i++)
if((sta>>i-1)&1)
all|=bit[i],sum++;
ans=min(ans,(int)all.count()/sum);
}
printf("%lld\n",ans*cnt);
}
return 0;
}
T4 半夜
解题思路
记 DP 数组\(f_{i,j,k}=\text{LCS}(S[i,j],T[1,k])\)
不难发现有如下性质:
\(f_{i-1,j,k}>f_{i-1,j-1,k}\Rightarrow f_{i,j,k}>f_{i,j-1,k}\)
\(f_{i,j,k}>f_{i,j,k-1}\Rightarrow f_{i-1,j,k}>f_{i-1,j,k-1}\)
那么就必然存在分界点 \(p_{k,j}\) 和 \(q_{k,j}\) 满足:
\]
设 \(F=f_{i,j-1,k-1}\)
就可以发现如下关系。
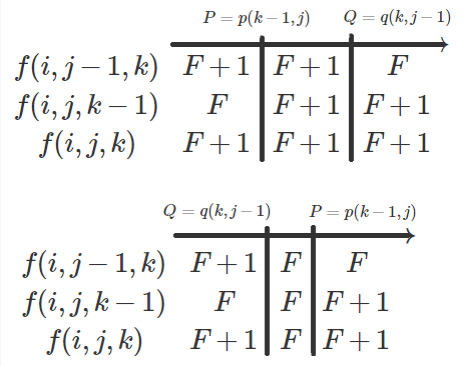
然后,我们就可以进而推出 p 与 q 。。。
code
#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define f() cout<<"Pass"<<endl
using namespace std;
const int N=2e3+10;
int n,ans,p[N][N<<1],q[N][N<<1];
char ch1[N],ch2[N<<1];
signed main()
{
scanf("%lld%s%s",&n,ch1+1,ch2+1);
for(int i=1;i<=n;i++)
ch2[i+n]=ch2[i];
for(int i=1;i<=2*n;i++)
p[0][i]=i;
for(int i=1;i<=n;i++)
for(int j=1;j<=2*n;j++)
{
p[i][j]=p[i-1][j]; q[i][j]=q[i][j-1];
if(ch1[i]==ch2[j]||p[i][j]<=q[i][j]) swap(p[i][j],q[i][j]);
}
for(int i=1,sum;i<=n;i++)
{
sum=0;
for(int j=i;j<i+n;j++)
sum+=(i>p[n][j]);
ans=max(ans,sum);
}
printf("%lld",ans);
return 0;
}
8.16考试总结(NOIP模拟41)[你相信引力吗·marshland·party?·半夜]的更多相关文章
- 2021.8.16考试总结[NOIP模拟41]
T1 你相信引力吗 肯定是单调栈维护.但存在重复值,还是个环,不好搞. 发现取区间时不会越过最大值,因此以最大值为断点将环断为序列.在栈里维护当前栈中有多少个与当前元素相等的元素,小分类讨论一下. 最 ...
- [考试总结]noip模拟41
发现长时间鸽博客会导致 rp--,所以今天来补一补 这个题目其实不是很毒瘤,然而是非常毒瘤... 题目不说请就是非常非常的烦人 首先 \(T1\) 就整整有两个歧义的地方,也就是说我们一共有 \(4\ ...
- 6.17考试总结(NOIP模拟8)[星际旅行·砍树·超级树·求和]
6.17考试总结(NOIP模拟8) 背景 考得不咋样,有一个非常遗憾的地方:最后一题少取膜了,\(100pts->40pts\),改了这么多年的错还是头一回看见以下的情景... T1星际旅行 前 ...
- 5.23考试总结(NOIP模拟2)
5.23考试总结(NOIP模拟2) 洛谷题单 看第一题第一眼,不好打呀;看第一题样例又一眼,诶,我直接一手小阶乘走人 然后就急忙去干T2T3了 后来考完一看,只有\(T1\)骗到了\(15pts\)[ ...
- 5.22考试总结(NOIP模拟1)
5.22考试总结(NOIP模拟1) 改题记录 T1 序列 题解 暴力思路很好想,分数也很好想\(QAQ\) (反正我只拿了5pts) 正解的话: 先用欧拉筛把1-n的素数筛出来 void get_Pr ...
- 2021.9.17考试总结[NOIP模拟55]
有的考试表面上自称NOIP模拟,背地里却是绍兴一中NOI模拟 吓得我直接文件打错 T1 Skip 设状态$f_i$为最后一次选$i$在$i$时的最优解.有$f_i=max_{j<i}[f_j+a ...
- [考试总结]noip模拟23
因为考试过多,所以学校的博客就暂时咕掉了,放到家里来写 不过话说,vscode的markdown编辑器还是真的很好用 先把 \(noip\) 模拟 \(23\) 的总结写了吧.. 俗话说:" ...
- 2021.7.15考试总结[NOIP模拟16]
ZJ模拟D2就是NB.. T1 Star Way To Heaven 谁能想到这竟是个最小生成树呢?(T1挂分100的高人JYF就在我身边 把上边界和下边界看成一个点和星星跑最小生成树,从上边界开始跑 ...
- Noip模拟41 2021.8.16
T1 你相信引力吗 对于区间的大小关系问题,往往使用单调栈来解决 这道题的优弧和劣弧很烦,考虑将其等价的转化 由于所有的合法情况绕过的弧都不会经过最高的冰锥, 又因为环可以任意亲定起点,这样可以直接把 ...
- 7.15考试总结(NOIP模拟16)[Star Way To Heaven·God Knows·Lost My Music]
败者死于绝望,胜者死于渴望. 前言 一看这个题就来者不善,对于第一题第一眼以为是一个大模拟,没想到是最小生成树. 对于第二题,先是看到了状压可以搞到的 20pts 然后对着暴力一顿猛调后来发现是题面理 ...
随机推荐
- 重新整理数据结构与算法(c#)—— 算法套路分治算法[二十五]
前言 有一个汉罗塔的游戏如下: 汉诺塔:汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具. 大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘. 大梵天 ...
- 深度解读《深度探索C++对象模型》之默认构造函数
接下来我将持续更新"深度解读<深度探索C++对象模型>"系列,敬请期待,欢迎关注!也可以关注公众号:iShare爱分享,主动获得推文. 提到默认构造函数,很多文章和书籍 ...
- 初探Mysql架构和InnoDB存储引擎
前言 mysql相信大家都不陌生了,分享之前我们先思考几个面试题: 1.undo log和redo log了解过吗?它们的作⽤分别是什么? 2.redo log是如何保证事务不丢失的? 3.mysql ...
- Worker 进行多线程任务开发
概念介绍 在 OpenHarmony 中,UI 线程负责处理 UI 事件和用户交互,而 Worker 线程用于处理耗时操作,以提高应用程序的响应速度和用户体验. Worker 线程是与主线程并行的独立 ...
- spring-jdbc5新特性,一个配置文件解决临时修改数据库的问题
import java.sql.SQLException; import java.util.List; import java.util.Map; import javax.sql.DataSour ...
- (二)asyncio的简单使用,python异步高效处理数据,asyncio.get_event_loop(),loop.run_until_complete(main()),loop.close()
Asyncio 是一个基于事件循环的异步I/O框架,它提供了高效的协程实现,能够轻松地编写高并发的Python程序.Asyncio 在 Python 3.4 中首次引入,它的核心是事件循环(Event ...
- 力扣633(java&python)-平方数之和(中等)
题目: 给定一个非负整数 c ,你要判断是否存在两个整数 a 和 b,使得 a2 + b2 = c . 示例 1: 输入:c = 5输出:true解释:1 * 1 + 2 * 2 = 5示例 2: 输 ...
- 直播回顾:准确性提升到 5 秒级,ssar 独创的 load5s 指标有多硬核?| 龙蜥技术
简介: 你还在为分析机器负载高而苦恼?这款 ssar 工具独创 load5s 指标精准定位超硬核. 编者按:本文整理自龙蜥SIG技术周会,作者闻茂泉,阿里云计算平台事业部SRE运维专家,是龙蜥社区跟 ...
- 聊聊 dotnet 7 对 bool 与字符串互转的底层性能优化
本文也叫 跟着 Stephen Toub 大佬学性能优化系列.大家都知道在 .NET 7 有众多的性能优化,其中就包括了对布尔和字符串互转的性能优化.在对布尔和字符串的转换的性能优化上,有着非常巧妙的 ...
- dotnet 读 WPF 源代码笔记 WriteableBitmap 的渲染和更新是如何实现
在 WPF 框架提供方便进行像素读写的 WriteableBitmap 类,本文来告诉大家在咱写下像素到 WriteableBitmap 渲染,底层的逻辑 之前我使用 WriteableBitmap ...
