ST 表

ST 表

定义

ST 表是用于解决 可重复贡献问题 的数据结构，通俗来说，一般可以解决区间查询问题。

区间最值和 \(gcd\)

我们以最大值为例，然后可以再推广到最小值和区间 \(gcd\)

首先你应该知道的是，ST表是利用倍增思想来缩短时间的。而倍增就体现在他数组的定义中：对于$f[i][j]$，指的是在序列的第i项，向后$2^j$个元素所包含序列间的最大值。

对于$i=1$，我们可以画出这么一个图，其下标即为$j$：

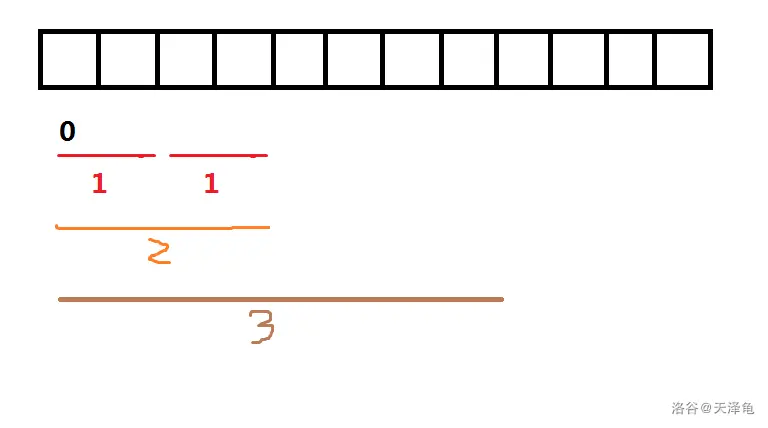
那么对于当前$i$转移其实很明显了，我们可以直接考虑将两个小区间的答案合并，即为这个大区间的值；如图中$f[1][2]$即可由$max(f[1][1],f[3][1])$转移来。

$$f[i][j]=max(f[i][j-1],f[i+2^{j-1}][j-1])$$

其中$2^{j-1}$也可写为$(1<<(j-1))$，这里位运算会更方便也会更快。

这个式子告诉我们，$ST$ 表类似于区间 $dp$，是由两个小区间合并上来的。所以应该先枚举区间长度l（这里即为$j$），再枚举$i$.

1. 然后一个问题应运而生了：我们这个转移方程有没有边界呢？

不妨来看一下$i=6$的图：

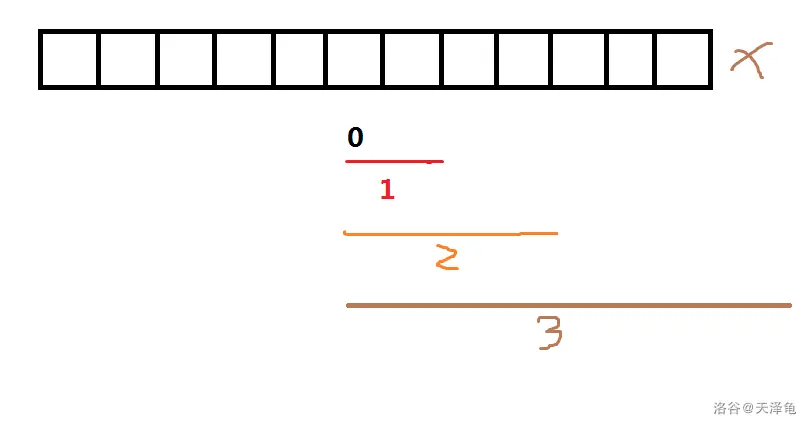
可以看出在$i=6$时，$j=3$的范围是$[6,13(6+2^3)]$，已经超出了我们数据的范畴。所以当$j=3$时，$i$只能取到$[1,5(12-2^3+1)]$

由上例再根据转移方程，不难看出当$j$确定时，$i$的范围受限在$[1,n-2^j+1]$。

我们现在来求红色标记区间$[L,R]$的最值。如果要最大化利用ST表，仍应该考虑类似处理ST表的方法，将该区间分成 两个ST表可直接维护的小区间，然后二者求最值即可。

• 那对于起始点，我们找一段ST表在该区间内可覆盖的，最大的子区间，由数学语言可描述为：

  $(L+2^k-1<=R) \Leftrightarrow (k<=lg[R-L+1])$ 那我们直接取等,令$j=k$即可~

于是对于起始点点在ST表里的取值即为：$f[L][k]$

• 对于终止点，我们反向找一个与起始点要求相同的子区间，由于对称性，此时k仍为起始点求得的$k=lg[R-L+1]$

但是我们应该如何确定该子区间的起点呢？由于子区间长度为$2^k$，设起点在$D$处，则满足：

$(D+2^k-1=R) \Leftrightarrow (D=R-2^k+1)$

于是对于终止点在ST表里的取值即为：$f[D][k]$，可证明这样一定可以覆盖整个区间。

综上，对于区间$[L,R]$求其最值，不难发现答案即为：

$$\max(f[L][k],f[R-(1<<k)+1][k])$$

同理，求 \(min\) 和 \(gcd\) 的过程和以上过程是一样的，在这里附上 P3865 的代码

模板题代码

给定一个长度为 \(N\) 的数列，和 $ M $ 次询问，求出每一次询问的区间内数字的最大值。

第一行包含两个整数 \(N,M\)，分别表示数列的长度和询问的个数。

第二行包含 \(N\) 个整数（记为 \(a_i\)），依次表示数列的第 \(i\) 项。

接下来 \(M\) 行，每行包含两个整数 \(l_i,r_i\)，表示查询的区间为 \([l_i,r_i]\)。

输出包含 \(M\) 行，每行一个整数，依次表示每一次询问的结果。

#include <bits/stdc++.h>
#define rint register int
#define endl '\n'
using namespace std;
const int N = 1e6 + 5;
const int M = 2e1 + 1;
int n, m;
int gcd_[N][M];
int maxx[N][M];
int minn[N][M];
int gcd(int a, int b)
{
	if (!b) return a;
	return gcd(b, a % b);
}
int query_gcd(int l, int r, int *a)
{
	int k = log2(r - l + 1);
	return gcd(a[l * M + k], a[(r - (1 << k) + 1) * M + k]);
}
int query_max(int l, int r, int *a)
{
    int k = log2(r - l + 1);
    return max(a[l * M + k], a[(r - (1 << k) + 1) * M + k]);
}
int query_min(int l, int r, int *a)
{
	int k = log2(r - l + 1);
	return min(a[l * M + k], a[(r - (1 << k) + 1) * M + k]);
}
signed main()
{
    cin >> n >> m;
    for (rint i = 1; i <= n; i++)
    {
    	int k;
    	cin >> k;
    	maxx[i][0] = k;
        minn[i][0] = k;
        gcd_[i][0] = k;
	}
    for (rint j = 1; j <= M; j++)
    {
        for (rint i = 1; i + (1 << j) - 1 <= n; i++)
		{
            int k = i + (1 << (j - 1));
			maxx[i][j] = max(maxx[i][j - 1], maxx[k][j - 1]);
			minn[i][j] = min(minn[i][j - 1], minn[k][j - 1]);
			gcd_[i][j] = gcd(gcd_[i][j - 1], gcd_[k][j - 1]);
		}
	}
    for (rint i = 1; i <= m; i++)
    {
        int l, r;
        cin >> l >> r;
        cout << query_max(l, r, (int *)maxx) << endl;
        //cout << query_min(l, r, (int *)minn) << endl;
        //cout << query_gcd(l, r, (int *)gcd_) << endl;
    }
    return 0;
}

[NOI2010] 超级钢琴

有 $n$ 个音符，编号为 $1$ 至 $n$ 。第 $i$ 个音符的美妙度为 $A_i$ 。

我们要找到 $k$ 段超级和弦组成的乐曲，每段连续的音符的个数 $x$ 满足 $L\leq x\leq R$ ，求乐曲美妙度的最大值。

首先，对于一段区间在左端点固定的情况下它的取值范围为 $sum[i + k]-sum[i - 1]\sim sum[i + k]-sum[i-1]$ 之间，$k\subseteq [l, r]$.所以，我们只需让前面一项最大即可。

ST 表维护一个前缀最大值，让后，每次取出使区间和最大的端点，再用前缀和计算区间和。这里用优先队列可以做到这点，同时用类似 ST 表的方法维护一个区间和最大的端点。

再考虑，由于不能出现两个相同的区间，所以取完一个区间后，设 $now$ 为选择的节点，它会分裂成两个区间。即 $l\sim now - 1$ 和 $now + 1\sim r$。判断是否合法之后加入优先队列，取 $k$ 次，就是最大值。

#include <bits/stdc++.h>
#define rint register int
#define int long long
#define endl '\n'
using namespace std;
const int N = 5e5 + 5;
const int M = 2e1 + 1;
int n, m, L, R;
int a[N], s[N];
int f[N][M];
int ans;
struct node
{
    int l, r, p, q;
    //p 是左端点, l 和 r 是右端点的范围, q 是当前解的右端点的位置
    bool operator < (const node &x) const
	{
        return s[x.q] - s[x.p] > s[q] - s[p];
    }
};
priority_queue<node> q;
int max(int a, int b)
{
	return a > b ? a : b;
}
int min(int x, int y)
{
    return s[x] < s[y] ? x : y;
}
int query_min(int l, int r, int *a)
{
    int k = log2(r - l + 1);
    return min(a[l * M + k], a[(r - (1 << k) + 1) * M + k]);
}
signed main()
{
    cin >> n >> m >> L >>R;
    for (rint i = 1; i <= n; i++)
    {
        cin >> a[i];
	}
    for (rint i = 1; i <= n; i++)
	{
        s[i] = s[i - 1] + a[i];
        f[i][0] = i;
    }
    for (rint j = 1; j <= M; j++)
    {
        for (rint i = 0; i + (1 << j) - 1 <= n; i++)
		//如果你在前面找最小值, ST 表要从 0 开始初始化
		{
            int k = i + (1 << (j - 1));
			f[i][j] = min(f[i][j - 1], f[k][j - 1]);
		}
	}
    for (rint i = L; i <= n; i++)
	{
        int r = i - L;
		int l = max(0, i - R);
        q.push({l, r, query_min(l, r, (int *)f), i});
    }
    for (rint i = 1; i <= m; i++)
	{
        node k = q.top();
        q.pop();
        ans += s[k.q] - s[k.p];
        int l = k.l;
		int r = k.p - 1;
        if (l <= r)
		{
			q.push({l, r, query_min(l, r, (int *)f), k.q});
		}
        l = k.p + 1;
		r = k.r;
        if (l <= r)
		{
			q.push({l, r, query_min(l, r, (int *)f), k.q});
		}
    }
    cout << ans << endl;
    return 0;
}