霍夫曼（最优二叉树）和Java达到

一、定义

一些定义：

• 节点之间的路径长度：在从节点树中的一个节点也经历分公司，这构成的两个节点之间的路径分支的数目后这就是所谓的路径长度
• 的路径长度：从树的根节点到树中每一结点的路径长度之和。

  在结点数目同样的二叉树中，全然二叉树的路径长度最短。

• 结点的权：在一些应用中，赋予树中结点的一个有某种意义的实数。
• 结点的带权路径长度：结点到树根之间的路径长度与该结点上权的乘积。
• 树的带权路径长度(Weighted Path Length of Tree：WPL)：定义为树中全部叶子结点的带权路径长度之和

如以下的二叉树，叶子节点的权值分别为5、6、2、4、7，的带权路径长度计算：

• 最优二叉树：从已给出的目标带权结点(单独的结点) 经过一种方式的组合形成一棵树.使树的权值最小.。最优二叉树是带权路径长度最短的二叉树。依据结点的个数，权值的不同，最优二叉树的形状也各不同样。它们的共同点是：带权值的结点都是叶子结点。

  权值越小的结点，其到根结点的路径越长。

如，给定4个叶子结点a，b，c和d，分别带权7。5。2和4。

构造例如以下图所看到的的三棵二叉树(还有很多棵)，它们的带权路径长度分别为：

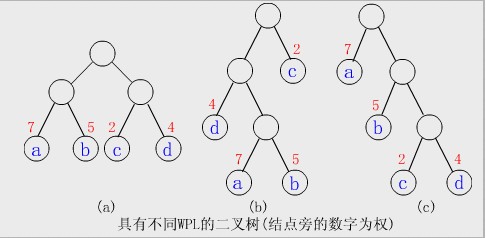
(a)WPL=7*2+5*2+2*2+4*2=36

        (b)WPL=7*3+5*3+2*1+4*2=46

        (c)WPL=7*1+5*2+2*3+4*3=35

当中(c)树的WPL最小。能够验证，它就是哈夫曼树。

注意：

    ① 叶子上的权值均同样时，全然二叉树一定是最优二叉树。否则全然二叉树不一定是最优二叉树。

    ② 最优二叉树中，权越大的叶子离根越近。

    ③ 最优二叉树的形态不唯一。WPL最小。

二、构造哈夫曼树

1） 依据给定的n个权值｛w1。 w2， w3， w4......wn｝构成n棵二叉树的森林 F=｛T1 ， T2 ， T3.....Tn｝。当中每棵二叉树仅仅有一个权值为wi 的根节点，其左右子树都为空；

2） 在森林F中选择两棵根节点的权值最小的二叉树，作为一棵新的二叉树的左右子树，且令新的二叉树的根节点的权值为其左右子树的权值和；

3）从F中删除被选中的那两棵子树。而且把构成的新的二叉树加到F森林中；

4）反复2 。3 操作，直到森林仅仅含有一棵二叉树为止。此时得到的这棵二叉树就是哈夫曼树。

构造步骤例如以下图：

三、Java实现

对指定节点创建哈夫曼树：

package com.liuhao.DataStructures;

import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.List;
import java.util.Queue;

public class HuffmanTree {

	public static class Node<E> {
		E data;
		double weight;
		Node leftChild;
		Node rightChild;

		public Node(E data, double weight) {
			super();
			this.data = data;
			this.weight = weight;
		}

		public String toString() {
			return "Node[data=" + data + ", weight=" + weight + "]";
		}
	}

	public static void main(String[] args) {
		List<Node> nodes = new ArrayList<Node>();

		nodes.add(new Node("A", 40.0));
		nodes.add(new Node("B", 8.0));
		nodes.add(new Node("C", 10.0));
		nodes.add(new Node("D", 30.0));
		nodes.add(new Node("E", 10.0));
		nodes.add(new Node("F", 2.0));

		Node root = HuffmanTree.createTree(nodes);

		System.out.println(breadthFirst(root));

	}

	/**
	 * 构造哈夫曼树
	 *
	 * @param nodes
	 *            节点集合
	 * @return 构造出来的哈夫曼树的根节点
	 */
	private static Node createTree(List<Node> nodes) {
		// 仅仅要nodes数组中还有2个以上的节点
		while (nodes.size() > 1) {
			quickSort(nodes);
			//获取权值最小的两个节点
			Node left = nodes.get(nodes.size()-1);
			Node right = nodes.get(nodes.size()-2);

			//生成新节点，新节点的权值为两个子节点的权值之和
			Node parent = new Node(null, left.weight + right.weight);

			//让新节点作为两个权值最小节点的父节点
			parent.leftChild = left;
			parent.rightChild = right;

			//删除权值最小的两个节点
			nodes.remove(nodes.size()-1);
			nodes.remove(nodes.size()-1);

			//将新节点增加到集合中
			nodes.add(parent);
		}

		return nodes.get(0);
	}

	/**
	 * 将指定集合中的i和j索引处的元素交换
	 *
	 * @param nodes
	 * @param i
	 * @param j
	 */
	private static void swap(List<Node> nodes, int i, int j) {
		Node tmp;
		tmp = nodes.get(i);
		nodes.set(i, nodes.get(j));
		nodes.set(j, tmp);
	}

	/**
	 * 实现高速排序算法，用于对节点进行排序
	 *
	 * @param nodes
	 * @param start
	 * @param end
	 */
	private static void subSort(List<Node> nodes, int start, int end) {
		if (start < end) {
			// 以第一个元素作为分界值
			Node base = nodes.get(start);
			// i从左边搜索，搜索大于分界值的元素的索引
			int i = start;
			// j从右边開始搜索，搜索小于分界值的元素的索引
			int j = end + 1;
			while (true) {
				// 找到大于分界值的元素的索引，或者i已经到了end处
				while (i < end && nodes.get(++i).weight >= base.weight)
					;
				// 找到小于分界值的元素的索引。或者j已经到了start处
				while (j > start && nodes.get(--j).weight <= base.weight)
					;

				if (i < j) {
					swap(nodes, i, j);
				} else {
					break;
				}
			}

			swap(nodes, start, j);

			//递归左边子序列
			subSort(nodes, start, j - 1);
			//递归右边子序列
			subSort(nodes, j + 1, end);
		}
	}

	public static void quickSort(List<Node> nodes){
		subSort(nodes, 0, nodes.size()-1);
	}

	//广度优先遍历
	public static List<Node> breadthFirst(Node root){
		Queue<Node> queue = new ArrayDeque<Node>();
		List<Node> list = new ArrayList<Node>();

		if(root!=null){
			//将根元素增加“队列”
			queue.offer(root);
		}

		while(!queue.isEmpty()){
			//将该队列的“队尾”元素增加到list中
			list.add(queue.peek());
			Node p = queue.poll();

			//假设左子节点不为null，将它增加到队列
			if(p.leftChild != null){
				queue.offer(p.leftChild);
			}

			//假设右子节点不为null。将它增加到队列
			if(p.rightChild != null){
				queue.offer(p.rightChild);
			}
		}

		return list;
	}
}

以上代码中的关键步骤包含：

（1）对list集合中全部节点进行排序；

（2）找出list集合中权值最小的两个节点。

（3）以权值最小的两个节点作为子节点创建新节点；

（4）从list集合中删除权值最小的两个节点，将新节点加入到list集合中

程序採用循环不断地运行上面的步骤，直到list集合中仅仅剩下一个节点，最后剩下的这个节点就是哈夫曼树的根节点

四、哈夫曼编码

依据哈夫曼树能够解决报文编码的问题。如果须要把一个字符串，如“abcdabcaba”进行编码，将它转换为唯一的二进制码。可是要求转换出来的二进制码的长度最小。

如果每一个字符在字符串中出现频率为W。其编码长度为L，编码字符n个，则编码后二进制码的总长度为W₁L₁+W₂L₂+…+W_nL_n。这恰好是哈夫曼树的处理原则。

因此能够採用哈夫曼树的构造原理进行二进制编码，从而使得电文长度最短。

对于“abcdabcaba”。共同拥有a、b、c、d4个字符。出现次数分别为4、3、2、1,相当于它们的权值，将a、b、c、d以出现次数为权值构造哈夫曼树，得到下左图的结果。

从哈夫曼树根节点開始，对左子树分配代码“0”，对右子树分配“1”，一直到达叶子节点。

然后，将从树根沿着每条路径到达叶子节点的代码排列起来，便得到每一个叶子节点的哈夫曼编码。例如以下右图。

从图中能够看出，a、b、c、d相应的编码分别为0、10、110、111，然后将字符串“abcdabcaba”转换为相应的二进制码就是0101101110101100100，只有长度19。这是最短的二进制编码。也被称为Huffman编码。

版权声明：本文博主原创文章，博客，未经同意不得转载。