Chapter 2 简单DC-DC变换器稳态分析小结

Chapter 2 简单DC-DC变换器稳态分析小结

1 本章重点

1.1 小纹波近似

所谓小纹波近似就是DC-DC变换器的稳态分析中，假定开关频率次的纹波相对于直流分量而言非常小，可以将其忽略进行各直流分量的计算。

例：Buck变换器输出电压包含直流分量\(V\)以及开关频率纹波\(v_{ripple}(t)\)

\[v(t) = V+v_{ripple}(t) \tag{1}
\]

应用小纹波近似后

\[v(t) \approx V \tag{2}
\]

1.2 电感伏秒平衡

首先我们知道电感的电压电流关系式为

\[v_{L}(t) = L \frac{d_{i}(t)}{dt} \tag{3}
\]

对上式左右分别在一个开关周期内进行积分

\[\int _{0} ^{T_{s}} v_{L}(t)dt =L \int _{0} ^{T_{s}} d_{i}(t) \tag{4}
\]

由于变换器稳态工作时，电感电流一个周期内变化量为0，即

\[\int _{0} ^{T_{s}} v_{L} (t) dt =0 \tag{5}
\]

1.3 电容电荷平衡

同样的，电容电压电流关系为

\[i_{C}(t) = C \frac{d u_{C}(t)}{dt} \tag{6}
\]

上式左右分别在一个周期内积分

\[\int _{0}^{T_{s}} i_{C}(t) dt =C \int _{0} ^{T_{s}} d u_{C}{t} \tag{7}
\]

同理，变换器稳态工作时，电容电压在一个周期内变化量也为0，即

\[\int _{0} ^{T_{s}} i_{C}(t)dt =0 \tag{8}
\]

1.4 电容定义式

分析电容状态时，还可能用到电容定义式

\[C= \frac{ \Delta Q}{\Delta V} \tag{9}
\]

上式中，\(\Delta Q\)为电荷量变化量，\(\Delta V\)为电容电压变化量

2 分析方法

对于Buck，Boost，Buck-Boost以及Cuk电路中均只有一个开关管，这里可以按照开关管工作状态将整个电路分为开关管导通与开关管关断两个状态。

对于整个电路分析，根据前节的几个电感及电容相关原理，以稳态下电感电压及电容电流一个周期内变化值为0作为分析切入点，列写相应的伏秒平衡，电容电荷平衡等式。

然后求解相应的电流，输出电压以及电感电流纹波，电容电压纹波等参数。

3 Buck电路分析

如图1所示为Buck变换器示意图，此后对CCM状态下电路进行分析。

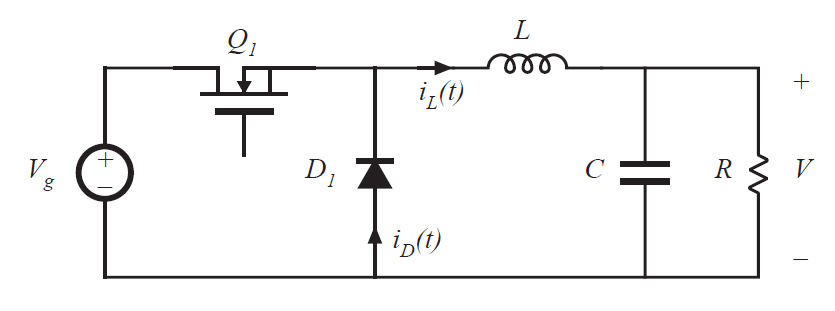
图1 Buck电路示意图

根据开关管的导通状态，分为导通和关断两个阶段对电路进行分析：

这里设电感电流直流量为\(I\)，输出电压直流量为\(V\)。

\(Q_{1}\)导通时(\(0<t<D T_{s}\))：

电感电压(左正右负)

\[v_{L} = V_{g}-V \tag{10}
\]

电容电流(向下为正)

\[i_{C} = I-\frac{V}{R} \tag{11}
\]

\(Q_{1}\)关断时(\(DT_{s}<t<T_{s}\))：

电感电压(左正右负)

\[v_{L} =-V \tag{12}
\]

电容电流(向下为正)

\[i_{C} = -\frac{V}{R} \tag{13}
\]

将式(10)-(13)分别代入伏秒平衡及电荷平衡公式有：

\[\int _{0} ^{T_{s}} v_{L} (t) dt =(V_{g}-V)DT_{s}-V(1-D)T_{s}=0 \\\int _{0} ^{T_{s}} i_{C}(t)dt =(I- \frac{V}{R} )DT_{s} -\frac{V}{R}(1-D)T_{s} = 0 \tag{14}
\]

根据式(14)，可以求解出Buck变换器输出电压直流分量以及电感电流的直流分量值

\[V=DV_{g} \\I=\frac{ DV_{g}}{R}\tag{15}
\]

此外，为了设计电感及电容，还要计算电感电流纹波及电容电压纹波。

电感电流纹波\(\Delta i_{L}\)计算原理可以根据稳态时电感电流在一个周期内变化量为0计算，即开关管导通或关断间隔内，电感电流的变化量相等。以开关管导通为例：根据式(3)可以有

\[V_{g}-V =L \frac{ 2 \Delta i_{L}}{DT_{s}} \tag{16}
\]

则电感电流纹波\(\Delta i_{L}\)为

\[\Delta i_{L} =\frac{V_{g}-V}{2L} DT_{s} = \frac{(1-D)V_{g}DT_{s}}{2L} \tag{17}
\]

对于电容电压纹波\(\Delta v\)，通过电荷平衡进行计算。假定电容\(C\)非常大，那么电感\(L\)上的纹波不会流经负载\(R\)，全部从电容\(C\)流过，也就是电容流过的电流为电感实际电流\(i_{L}\)减去直流分量\(I\)后的纹波电流，如图2所示。电容电压也就是在输出电压的直流分量\(V\)上有\(\Delta v\)的波动。

图2 电容电流及电压波形

其中，当电容电流为正时，电容充电，电压升高，且一个开关周期内，电容电压升高与下降幅值相同。根据图2可以知道，电流阴影部分对应的积分值即为电容在该时段内的电荷变化量。根据电流变化的对称性我们还可以知道该段时间长度为\(T_{s}/2\)。计算其面积为：

\[q = \frac{1}{2} \frac{T_{S}}{2} \Delta i_{L} \tag{18}
\]

再根据式(9)，可以得到电容电压纹波值为：

\[\Delta v = \frac{\Delta i_{L} T_{s}}{8C} \tag{19}
\]

将式(17)代入式(19)，得到

\[\Delta v = \frac{D(1-D) V_{g} {T_{s}}^2}{16LC} \tag{20}
\]

为了验证上述分析的正确性，我们根据下表的参数进行仿真：

变量	值
\(V_{g} /V\)	100
\(T_{s} /s\)	0.0002
\(D\)	0.5
\(L/mH\)	5
\(C/ \mu F\)	100
\(R/ \Omega\)	10

表1 Buck变换器参数表

根据式(15),(17)以及(20)，计算相应输出电压，电感电流，电感电流纹波以及电容电压纹波大小

\[V = D V_{g} =0.5*100=50V \\I = \frac{ DV_{g}}{R} = \frac{ 0.5*100}{10}=5 A \\\Delta i_{L} = \frac{(1-D)V_{g}DT_{s}}{2L} = \frac{0.5*100*0.5*0.0002}{2*0.005}=0.5A \\\Delta v = \frac{D(1-D) V_{g} {T_{s}}^2}{16LC} = \frac{0.5*0.5*100*0.002*0.002}{16*0.005*0.0001} = 0.125V \tag{21}
\]

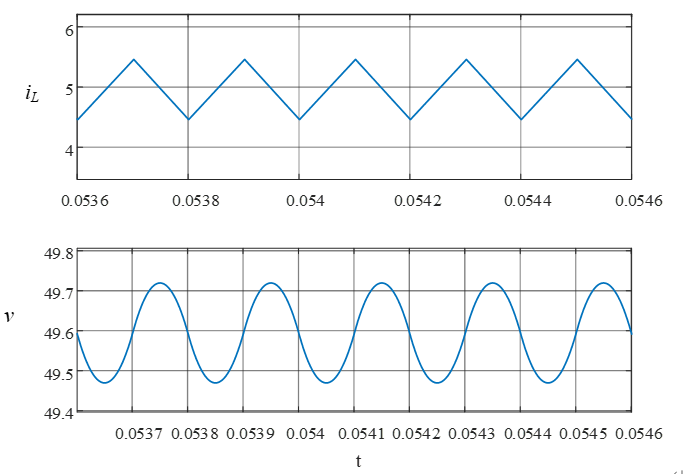
图3 Buck变换器电感电流及输出电压波形图

图中所示为Buck变换器的电感电流波形与输出电压波形，与计算结果相吻合，可以证明计算结果的正确性。

4 Boost电路分析

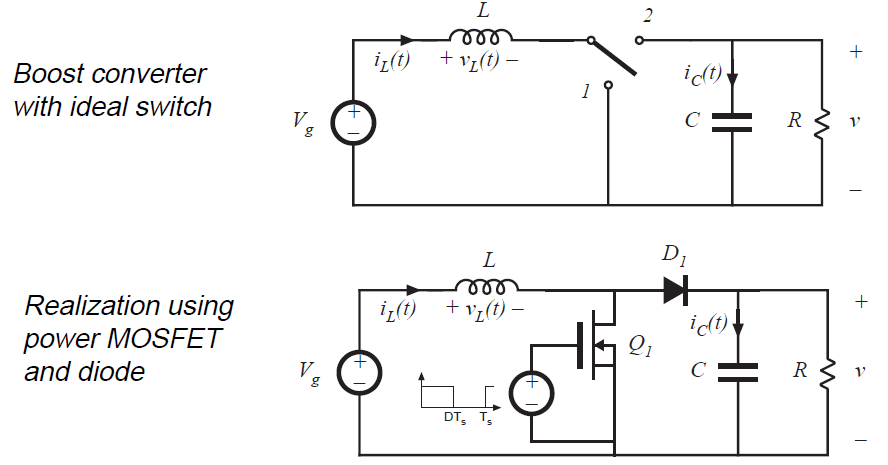
图4 Boost电路示意图

如图4所示为Boost电路示意图，

同理，这里设电感电流直流量为\(I\)，输出电压直流量为\(V\)。

\(Q_{1}\)导通时(\(0<t<D T_{s}\))：

电感电压(左正右负)

\[v_{L} = V_{g} \tag{22}
\]

电容电流(向下为正)

\[i_{C} = -\frac{V}{R} \tag{23}
\]

\(Q_{1}\)关断时(\(DT_{s}<t<T_{s}\))：

电感电压(左正右负)

\[v_{L} =V_{g}-V \tag{24}
\]

电容电流(向下为正)

\[i_{C} = I-\frac{V}{R} \tag{25}
\]

将式(22)-(25)分别代入伏秒平衡及电荷平衡公式有：

\[\int _{0} ^{T_{s}} v_{L} (t) dt =V_{g}DT_{s}+(V_{g}-V)(1-D)T_{s}=0 \\\int _{0} ^{T_{s}} i_{C}(t)dt =(- \frac{V}{R} )DT_{s} +(I-\frac{V}{R})(1-D)T_{s} = 0 \tag{26}
\]

根据式(14)，可以求解出Boost变换器输出电压直流分量以及电感电流的直流分量值

\[V=\frac{V_{g}}{1-D} \\I=\frac{ V_{g}}{(1-D)^2 R}\tag{27}
\]

同理，开关管导通时，电感电流纹波\(\Delta i_{L}\)可以计算为

\[V_{g} = L \frac{2 \Delta i_{L}}{D T_{s}} \tag{28}
\]

则

\[\Delta i_{L} = \frac{V_{g} D T_{s}}{2L} \tag{29}
\]

而电容电压纹波可以根据电荷平衡，利用导通时的电容电流

\[- \frac{V}{R}= C \frac{-2 \Delta v}{D T_{s}} \tag{30}
\]

电容电压纹波为

\[\Delta v = \frac{V}{2RC} D T_{s}=\frac{V_{g}}{2(1-D)RC} D T_{s} \tag{31}
\]

实际上这里Boost电路输出滤波电容纹波计算方式与Buck电路输出滤波电容计算不同，是由于Buck电路输出滤波电路中电感\(L\)与电容\(C\)形成了二极点，小纹波近似失效，所以二者计算方式不同。

Boost电路参数设置同表1，计算相应的电感电流，输出电压，电感电流纹波以及电容电压纹波

\[V = \frac{V_{g}}{1-D} =\frac{100}{1-0.5}=200V \\I = \frac{ V_{g}}{(1-D)^2 R} = \frac{ 100}{(1-0.5)^2 10}=40 A \\\Delta i_{L} = \frac{V_{g}DT_{s}}{2L} = \frac{100*0.5*0.0002}{2*0.005}=1A \\\Delta v = \frac{V_{g}DT_{s}}{2(1-D)RC} = \frac{100*0.5*0.0002}{2*0.5*10*0.0001}=10V \tag{32}
\]

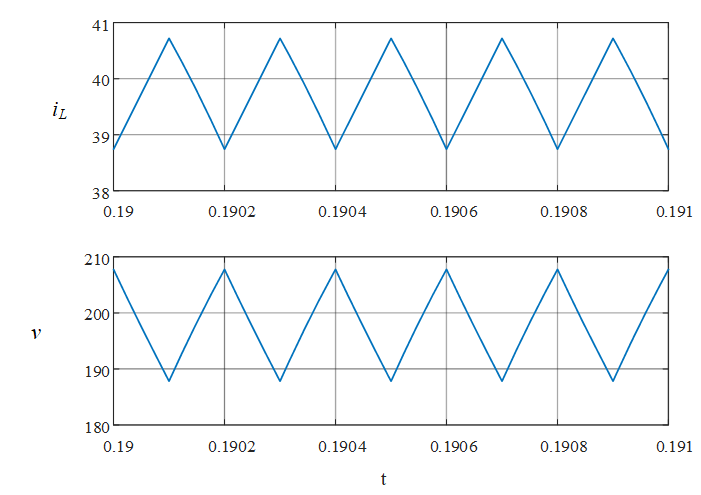
图4 变换器电感电流及输出电压波形图