前缀和线性基HDU6579

Operation

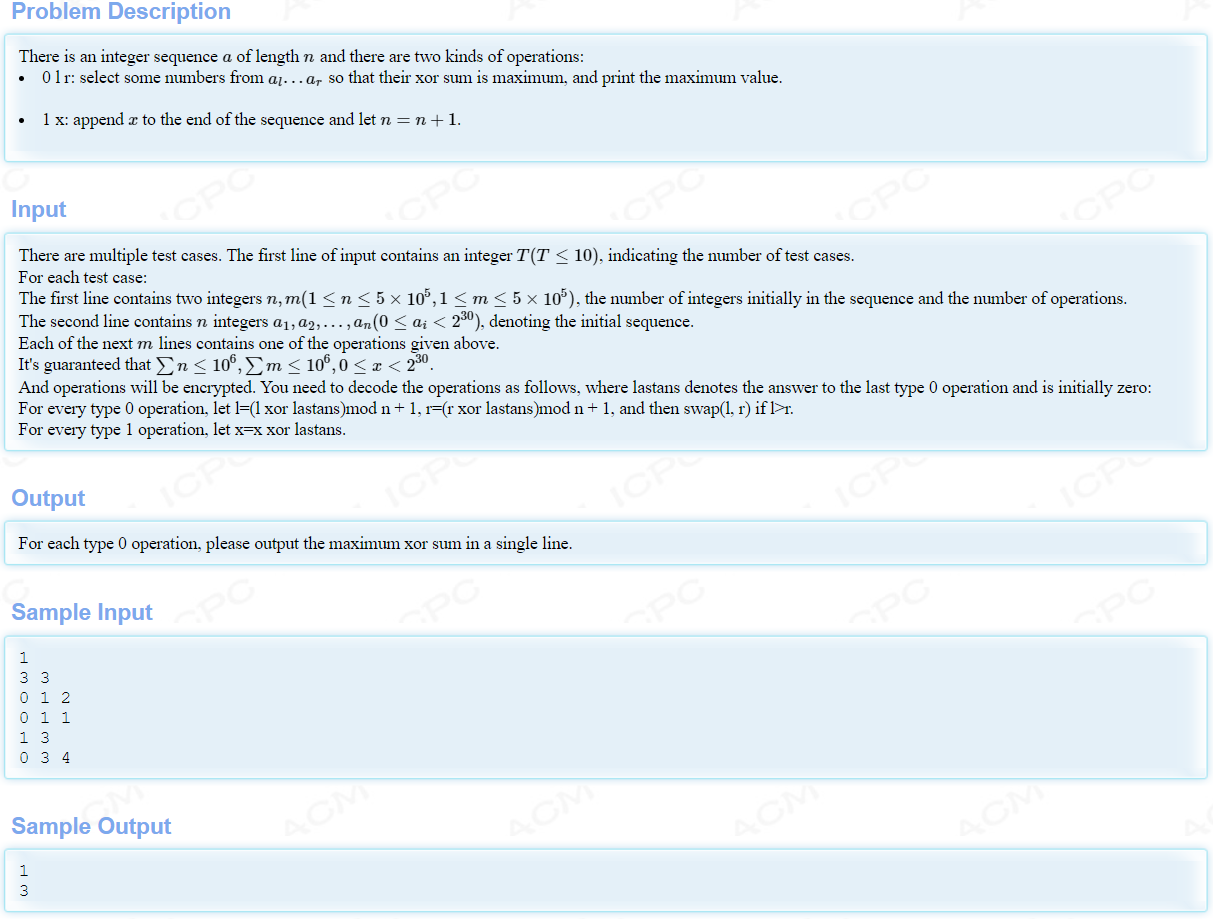
题解：看到区间最大异或和，首先想到的是线性基；

线性基可以处理的操作是：

• 在数列末尾插入一个数
• 查询全局的子集异或最大值

由于线性基的长度很短，因此我们可以将数列所有前缀的线性基保存下来。1到x的线性基可以由1到x-1的线性基通过插入a[x]来求得，这样，我们就可以查询前缀区间的子集异或最大值。现在问题的关键在于，查询区间 [L, R] 时，如何避免 [1, L-1] 的干扰。

考虑线性基的插入过程，如果线性基当前位上已经有值，我们就不能把待插入的值放入这一位，因此线性基上每一位的数，都是对应位上在原数列最左侧的数字。现在我们改变策略，使得线性基上每一位的数，都变成对应位上在原数列最右侧的数字。实现这个策略的方法是：我们额外保存线性基上每一位数在原数列中的位置，插入的时候，如果对应位上的数在原数列中更靠左，就用待插入的数和它交换。基于这种策略，我们在查询区间 [L, R] 时，可以在区间 [1, R] 对应的线性基中查询，对于线性基上每一位的数，如果它在原数组中出现的位置比 L 更靠右，就考虑它对答案的贡献，否则直接跳过这一位。

这个做法的正确性也很显然，通过改变策略，使线性基上每一位数变成对应位上在原数列最右侧的数字，可以看成线性基插入数字的顺序变反，完全不影响线性基的性质。同时，将线性基上所有在原数组中的位置比 x 更靠左的数字删除，可以视为区间 [1, L-1] 的数字还没有被插入线性基。

复杂度：O((n + m) logx)，n为初始数列长度，m为操作次数，x为值域大小。

大佬的博客讲解：here

AC_Code:

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 using namespace std;
 typedef long long ll;
 #define endl '\n'
 const int maxn = ;
 const int maxm = 5e5+;
 const int inf = 0x3f3f3f3f;

 int cnt;//当前已插入的数的个数
 int a[maxm][maxn];//保存所有前缀区间的线性基
 int b[maxm][maxn];//保存线性基上的数字在原数组上的对应位置
 int n,m;

 void LB(int x){
     int cur=++cnt;//表示待插入的数字在原数组上的位置
     for(int i=;i>=;i--){
         a[cnt][i]=a[cnt-][i];
         b[cnt][i]=b[cnt-][i];
     }
     for(int i=;i>=;i--){
         if( !(x>>i) ) continue;
         if( !a[cnt][i] ){
             a[cnt][i]=x;
             b[cnt][i]=cur;
             break;
         }
         else{
             if( cur>b[cnt][i] ){    //如果待插入的数字在原数组上更靠右,则用线性基上的数与其交换
                 swap(a[cnt][i],x);
                 swap(b[cnt][i],cur);    //位置也要交换
             }
             x^=a[cnt][i];
         }
     }
 }

 int query(int l,int r){
     l=l%cnt+; r=r%cnt+;   //注意这里是%cnt,不是%n
     if( l>r ) swap(l,r);
     int ret=;
     for(int i=;i>=;i--){
         if( b[r][i]>=l ){   //如果在原数组中的位置比l更靠右,那么就产生贡献,此处b[r][i]就已经限制了右区间
             ret=max(ret,ret^a[r][i]);   //线性基贪心求最大值的基本操作
         }
     }
     return ret;
 }

 int main()
 {
     int t; scanf("%d",&t);
     while( t-- ){
         cnt=;
         scanf("%d%d",&n,&m);
         for(int i=;i<n;i++){
             int a;
             scanf("%d",&a);
             LB(a);
         }
         int lastans=, opt, x, y;   //lastans用于处理强制在线
         for(int i=;i<m;i++){
             scanf("%d%d",&opt,&x);
             if( opt== ){
                 scanf("%d",&y);
                 x=x^lastans;
                 y=y^lastans;
                 lastans = query(x, y);
                 printf("%d\n",lastans);
             }
             else{
                 LB(x^lastans);
             }
         }
     }
     return ;
 }