Leetcode-二分

69. x的平方根 https://leetcode-cn.com/problems/sqrtx/

实现 int sqrt(int x) 函数。

计算并返回 x 的平方根，其中 x 是非负整数。

由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

解：

二分，不断枚举可能的结果，判断其平方和x的关系。这题二分的过程中考虑直接用浮点型来处理，比用整型处理更通用。

class Solution:
    def mySqrt(self, x: int) -> int:
        if x <= 1:
            return x

        low, high = 0., float(x)
        while abs(high - low) > 1e-5:
            mid = (high + low)/2
            y = mid*mid

            if y == float(x):
                return int(mid)
            elif y < float(x):
                low = mid  # 因为是浮点型，直接mid赋给low就行
            else:
                high = mid
        return int(high)

　　

牛顿迭代法，以直线代替曲线，用一阶泰勒展式（即在当前点的切线）代替原曲线，求直线与 x 轴的交点，重复这个过程直到收敛。

如果要求2的平方根，令f(x)=x² -2，如下图。

from https://leetcode-cn.com/problems/sqrtx/solution/niu-dun-die-dai-fa-by-loafer/

如何通俗易懂地讲解牛顿迭代法求开方？数值分析？ - 马同学的回答 - 知乎 https://www.zhihu.com/question/20690553/answer/146104283

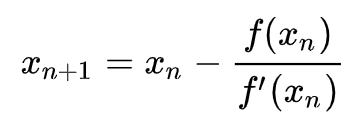
所以要求给定的 X 的平方根，x_n+1 = x_n -  (x_n² - X) / 2x_n ，迭代到满足逼近精度即可。考虑到这题要求向下取整。

class Solution:
    def mySqrt(self, x: int) -> int:
        if x <= 1:
            return x
        cur = x
        while True:
            pre = cur
            cur = (cur + x / cur) / 2
            if abs(cur - pre) < 1e-5:
                return int(cur)

　

367. 有效的完全平方数 https://leetcode-cn.com/problems/valid-perfect-square/

给定一个正整数 num，编写一个函数，如果 num 是一个完全平方数，则返回 True，否则返回 False。

说明：不要使用任何内置的库函数，如  sqrt。

解：

先按浮点型计算一下给定数的平方根，再取整后平方一下和num比较，相等的话即为完全平方数。

class Solution:
    def isPerfectSquare(self, num: int) -> bool:
        if num <= 1:
            return True
        low, high = 0., float(num)
        while abs(high - low) > 1e-5:
            mid = (high + low)/2
            y = mid*mid

            if y == float(num):
                return True
            elif y < float(num):
                low = mid
            else:
                high = mid

        return True if int(high) ** 2 == num else False

class Solution:
    def isPerfectSquare(self, num: int) -> bool:
        if num <= 1:
            return True
        cur = num
        while True:
            pre = cur
            cur = (cur +  num/cur) /2
            if abs(cur-pre) < 1e-5:
                return True if int(cur) ** 2 == num else False

　　

直接按整数二分，找不到整数平方根就不是完全平方数。

class Solution:
    def isPerfectSquare(self, num: int) -> bool:
        if num <= 1:
            return True
        low, high = 0, num
        while low <= high:
            mid = low + (high - low)//2
            y = mid ** 2
            if y < num:
                low = mid + 1
            elif y > num:
                high = mid - 1
            else:
                return True
        return False