poj2478 Farey Sequence (欧拉函数)

Farey Sequence

题意：给定一个数n，求在[1,n]这个范围内两两互质的数的个数。（转化为给定一个数n，比n小且与n互质的数的个数）

知识点：

欧拉函数：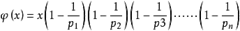

普通求法：

int Euler(int n)
{
    int ans=n;
    for(int i=0;i<cnt&&prime[i]<=n;i++)
    {
        if(n%prime[i]==0)
        {
            ans=ans-ans/prime[i];
            while(n%prime[i]==0)
                n/=prime[i];
        }
    }
    if(n==1)
        return ans;
    if(n>1)
        return ans-ans/n;

}

筛选法：（基于素数筛，跟着代码模拟一遍就懂）

void Init()
{

     for(int i=1;i<N;i++)
       euler[i]=i;
     for(int i=2;i<N;i++)                 //i=1时，euler[1] 不变
        if(euler[i]==i)
           for(int j=i;j<N;j+=i)
              euler[j]=euler[j]/i*(i-1);
}

题解：筛选法求欧拉函数

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=1e6+5;

int euler[N];

void Init()
{
     euler[1]=1;
     for(int i=2;i<N;i++)
       euler[i]=i;
     for(int i=2;i<N;i++)
        if(euler[i]==i)
           for(int j=i;j<N;j+=i)
              euler[j]=euler[j]/i*(i-1);
}

int main()
{
    Init();
    int n;
    while(cin>>n&&n)
    {
        long long ans=0;
        for(int i=2;i<=n;i++)
            ans+=euler[i];
        cout<<ans<<endl;
    }
}