Baby-step giant-step算法

写在前面：

　　学习笔记，方便复习，学习资料来自网络，注明出处

我们都在努力奔跑，我们都是追梦人

结论

　　In group theory, a branch of mathematics, the baby-step giant-step is a meet-in-the-middle algorithm for computing the discrete logarithm

　　The algorithm is based on a space–time tradeoff. It is a fairly simple modification of trial multiplication, the naive method of finding discrete logarithms

——Wikipedia

译：

　　在群论中，作为数学的一个分支，BSGS算法是计算离散对数的一种中间交集算法

　　该算法时间复杂度/空间复杂度相权衡。是对试乘法的一个相当简单的修改，这是一种求离散对数的幼稚方法

实现

• 裸的Baby-step giant-step算法

　　首先，要知道什么是[◹]离散对数

　　BSGS算法的输入输出：

　　　　输入：一个n阶的模群G，群元素β

　　　　输出：一个整数x，满足α^x ≡ β (G中)

　　实际上是[◹]拓展欧几里得算法的应用③

　　已知正整数a，b，素数p，保证给出的a，p互素，求一个整数x使满足a^x ≡ b (MOD p)

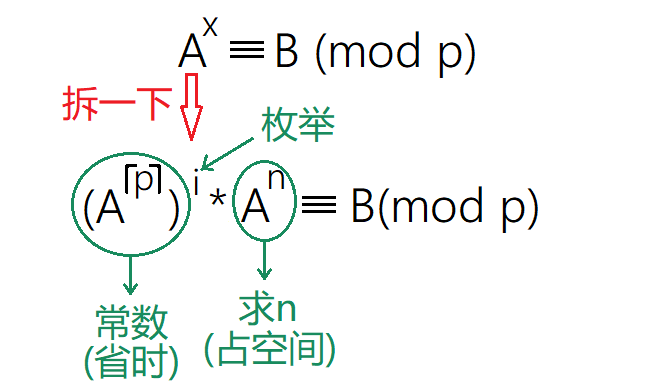
　　希望求得x，把x拆一下，拆成⌈p⌉*i+n

　　其中：

　　　　0<=i<⌈p⌉

　　　　0<=n<⌈p⌉

　　(A^⌈p⌉)ⁱ*Aⁿ ≡ B (mod p)

　　这里使用[◹]拓展欧几里得算法的应用②

　　因为p是质数，且a，p互素，保证了解的存在，自然能求出来一个解

　　如果需要多解，从小到大枚举i，那么得到的x也就从小到大

　　至于Aⁿ，知道了Aⁿ等于几，怎么知道n是几呢？

　　有一个很聪(diu)明(ren)的方法，事先把Aⁿ与n存到hash表(或者map)里(占一定时间)，查一下就好了

　　

　　当然，如果没有特别说明a，p互素，需要考虑不互素的情况，a是p的倍数或者a==0时(a%p==0)：

　　　　①b==1，则当a！=0时，除了零以外任何数的0次方都等于1，若a==0，无解

　　　　②b==0，则x可以取0以外任意正整数