Redis 集合统计（HyperLogLog）

统计功能是一类极为常见的需求，比如下面这个场景：

为了决定某个功能是否在下个迭代版本中保留，产品会要求统计页面在上新前后的 UV 作为决策依据。

简单来说就是统计一天内，某个页面的访问用户量，如果相同的用户再次访问，也只算记为一次访问。

下面我们将从这个场景出发，讨论如何选择的合适的 Redis 数据结构实现统计功能。

Redis与统计

聚合统计

要完成这个统计任务，最直观的方式是使用一个SET保存页面在某天的访问用户 ID，然后通过对集合求差SDIFF和求交SINTER完成统计：

# 2020-01-01 当日的 UV
SADD page:uv:20200101 "Alice" "Bob" "Tom" "Jerry"

# 2020-01-02 当日的 UV
SADD page:uv:20200102 "Alice" "Bob" "Jerry" "Nancy"

# 2020-01-02 新增用户
SDIFFSTORE page:new:20200102 page:uv:20200102 page:uv:20200101

# 2020-01-02 新增用户数量
SCARD page:new:20200102

# 2020-01-02 留存用户
SINTERSTORE page:rem:20200102 page:uv:20200102 page:uv:20200101

# 2020-01-02 留存用户数量
SCARD page:rem:20200102

优点：

• 操作直观易理解，可以复用现有的数据集合
• 保留了用户的访问细节，可以做更细粒度的统计

缺点：

• 内存开销大，假设每个用户ID长度均小于 44 字节（使用 embstr 编码），记录 1 亿用户也至少需要 6G 的内存
• SUNION、SINTER、SDIFF计算复杂度高，大数据量情况下会导致 Redis 实例阻塞，可选的优化方式有：
  • 从集群中选择一个从库专门负责聚合计算
  • 把数据读取到客户端，在客户端来完成聚合统计

二值统计

当用户 ID 是连续的整数时，可以使用BITMAP实现二值统计：

# 2020-01-01 当日的 UV
SETBIT page:uv:20200101 0 1 # "Alice"
SETBIT page:uv:20200101 1 1 # "Bob"
SETBIT page:uv:20200101 2 1 # "Tom"
SETBIT page:uv:20200101 3 1 # "Jerry"

# 2020-01-02 当日的 UV
SETBIT page:uv:20200102 0 1 # "Alice"
SETBIT page:uv:20200102 1 1 # "Bob"
SETBIT page:uv:20200102 3 1 # "Jerry"
SETBIT page:uv:20200102 4 1 # "Nancy"

# 2020-01-02 新增用户
BITOP NOT page:not:20200101 page:uv:20200101
BITOP AND page:new:20200102 page:uv:20200102 page:not:20200101 

# 2020-01-02 新增用户数量
BITCOUNT page:new:20200102

# 2020-01-02 留存用户
BITOP AND page:rem:20200102 page:uv:20200102 page:uv:20200101

# 2020-01-02 留存用户数量
BITCOUNT page:new:20200102

优点：

• 内存开销低，记录 1 亿个用户只需要 12MB 内存
• 统计速度快，计算机对比特位的异或运算十分高效

缺点：

• 对数据类型有要求，只能处理整数集合

基数统计

前面两种方式都能提供准确的统计结果，但是也存在以下问题：

• 当统计集合变大时，所需的存储内存也会线性增长
• 当集合变大时，判断其是否包含新加入元素的成本变大

考虑下面这一场景：

产品可能只关心 UV 增量，此时我们最终要的结果是访问用户集合的数量，并不关心访问集合里面包含哪些访问用户

只统计一个集合中不重复的元素个数，而并不关心集合元素内容的统计方式，我们将其称为基数计数cardinality counting

针对这一特定的统计场景，Redis 提供了HyperLogLog类型支持基数统计：

# 2020-01-01 当日的 UV
PFADD page:uv:20200101 "Alice" "Bob" "Tom" "Jerry"
PFCOUNT page:uv:20200101

# 2020-01-02 当日的 UV
PFADD page:uv:20200102 "Alice" "Bob" "Tom" "Jerry" "Nancy"
PFCOUNT page:uv:20200102

# 2020-01-01 与 2020-01-02 的 UV 总和
PFMERGE page:uv:union page:uv:20200101 page:uv:20200102
PFCOUNT page:uv:union

优点：

HyperLogLog计算基数所需的空间是固定的。只需要 12KB 内存就可以计算接近 \(2^{64}\) 个元素的基数。

缺点：

HyperLogLog的统计是基于概率完成的，其统计结果是有一定误差。不适用于精确统计的场景。

HyperLogLog 解析

概率估计

HyperLogLog是一种基于概率的统计方式，该如何理解？

我们来做一个实验：不停地抛一个均匀的双面硬币，直到结果是正面为止。

用 0 和 1 分别表示正面与反面，则实验结果可以表示为如下二进制串：

                +-+
第 1 次抛到正面   |1|
                +-+
                +--+
第 2 次抛到正面   |01|
                +--+
                +---+
第 3 次抛到正面   |001|
                +---+
                +---------+
第 k 次抛到正面   |000...001|  (总共 k-1 个 0)
                +---------+

由于每次抛硬币得到正面的概率均为$\frac{1}{2}$，因此实验在第 k 次结束的可能性为 $(\frac{1}{2})^k$（二进制串中首个 1 出现在第 k 位的概率）。

进行 n 实验后，将每次实验抛硬币的次数记为 \(k_1, k_3,\cdots,k_n\)，其中的最大值记为 \(k_{max}\)。

理想情况下有 \(k_{max} = log_2(n)\)，反过来也可以通过 \(k_{max}\) 来估计总的实验次数 \(n = 2^{k_{max}}\)。

处理极端情况

实际进行实验时，极端情况总会出现，比如在第 1 次实验时就连续抛出了 10 次反面。

如果按照前面的公式进行估计，会认为已经进行了 1000 次实验，这显然与事实不符。

为了提高估计的准确性，可以同时使用 m 枚硬币进行 分组实验。

然后计算这 m 组实验的平均值 \(\hat{k}_{max} = \frac{\sum_{i=0}^{m}{k_{max}}}{m}\)，此时能更准确的估计实际的实验次数 \(\hat{n}=2^{\hat{k}_{max}}\)。

基数统计

通过前面的分析，我们可以总结出以下经验：

可以通过二进制串中首个 1 出现的位置 \(k_{max}\) 来估计实际实验发生的次数 \(n\)

HyperLogLog借鉴上述思想来统计集合中不重复元素的个数：

• 使用 hash 函数集合中的每个元素映射为定长二进制串
• 利用 分组统计 的方式提高准确性，将二进制串分到 \(m\) 个不同的桶bucket中分别统计
  • 二进制串的前 \(log_2{m}\) 位用于计算该元素所属的桶
  • 剩余二进制位中，首个 1 出现的比特位记为 \(k\)，每个桶中的只保存最大值 \(k_{max}\)
• 当需要估计集合中包含的元素个数时，使用公式 \(\hat{n}=2^{\hat{k}_{max}}\) 计算即可

下面来看一个例子：

某个HyperLogLog实现，使用8bit 输出的 hash 函数并以 4 个桶进行分组统计

使用该 HLL 统计 Alice，Bob，Tom，Jerry，Nancy 这 5 个用户访问页后的 UV

                 映射为二进制串     分组    计算k
                      |            |       |
                      V            V       V
                 +---------+
hash("Alice") => |01|101000| => bucket=1, k=1
                 +---------+                                           分组统计 k_max
                 +---------+
hash("Bob")   => |11|010010| => bucket=3, k=2           +----------+----------+----------+----------+
                 +---------+                            | bucket_0 | bucket_1 | bucket_2 | bucket_3 |
                 +---------+                     ==>    +----------+----------+----------+----------+
hash("Tom")   => |10|001000| => bucket=2, k=3           | k_max= 1 | k_max= 2 | k_max= 3 | k_max= 2 |
                 +---------+                            +----------+----------+----------+----------+
                 +---------+
hash("Jerry") => |00|111010| => bucket=0, k=1
                 +---------+
                 +---------+
hash("Nancy") => |01|010001| => bucket=1, k=2
                 +---------+

分组计数完成后，用之前的公式估计集合基数为 \(2^{\hat{k}_{max}}= 2^{(\frac{1+2+3+2}{4})} = 4\)。

误差分析

在 Redis 的实现中，对于一个输入的字符串，首先得到 64 位的 hash 值：

• 前 14 位来定位桶的位置（共有16384个桶）
• 后 50 位用作元素对应的二进制串（用于更新首次出现 1 的比特位的最大值 \(k_{max}\)）

由于使用了 64 位输出的 hash 函数，因此可以计数的集合的基数没有实际限制。

HyperLogLog的标准误差计算公式为 \(\frac{1.04}{\sqrt{m}}\)（\(m\) 为分组数量），据此计算 Redis 实现的标准误差为 \(0.81\%\)。

下面这幅图展示了统计误差与基数大小的关系：

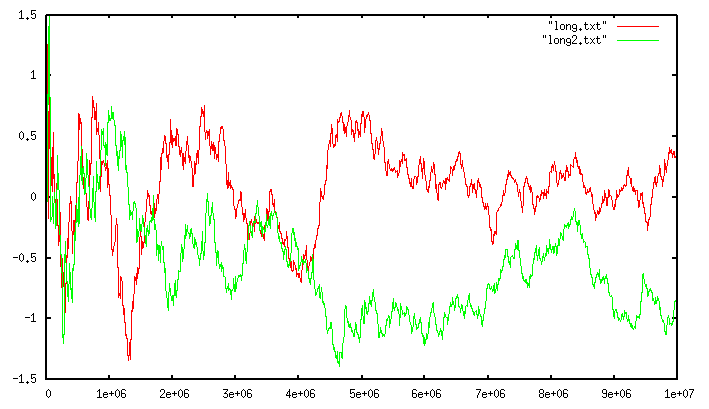
• 红线和绿线分别代表两个不同分布的数据集
• x 轴表示集合实际基数
• y 轴表示相对误差（百分比）

分析该图可以得出以下结论：

• 统计误差与数据本身的分布特征无关
• 集合基数越小，误差越小（小基数时精度高）
• 集合基数越大，误差越大（大基数时省资源）

参考资料

• http://antirez.com/news/75
• https://www.yuque.com/abser/aboutme/nfx0a4