PBR：基于物理的渲染(Physically Based Rendering)+理论相关

一： 关于能量守恒

1. 出射光线的能量永远不能超过入射光线的能量（发光面除外）。如图示我们可以看到，随着粗糙度的上升镜面反射区域的会增加，但是镜面反射的亮度却会下降。如果不管反射轮廓的大小而让每个像素的镜面反射强度(Specular Intensity)都一样的话，那么粗糙的平面就会放射出过多的能量，而这样就违背了能量守恒定律。这也就是为什么正如我们看到的一样，光滑平面的镜面反射更强烈而粗糙平面的反射更昏暗。
2. 当一束光线碰撞到一个表面的时候，它就会分离成一个折射部分和一个反射部分。反射部分就是会直接反射开来而不会进入平面的那部分光线，这就是我们所说的镜面光照。而折射部分就是余下的会进入表面并被吸收的那部分光线，这也就是我们所说的漫反射光照。
3. 通过物理学我们可以得知，光线实际上可以被认为是一束没有耗尽就不停向前运动的能量，而光束是通过碰撞的方式来消耗能量。每一种材料都是由无数微小的粒子所组成，这些粒子都能如下图所示一样与光线发生碰撞。这些粒子在每次的碰撞中都可以吸收光线所携带的一部分或者是全部的能量而后转变成为热量。
4. 一般来说，并非所有能量都会被全部吸收，而光线也会继续沿着（基本上）随机的方向发散，然后再和其他的粒子碰撞直至能量完全耗尽或者再次离开这个表面。而光线脱离物体表面后将会协同构成该表面的（漫反射）颜色。
5. 而有一些被称为次表面散射(Subsurface Scattering)技术的着色器技术将这个问题考虑了进去，它们显著的提升了一些诸如皮肤，大理石或者蜡质这样材质的视觉效果，不过伴随而来的则是性能下降代价。
6. 反射光与折射光之间的这个区别使我们得到了另一条关于能量守恒的经验结论：反射光与折射光它们二者之间是互斥的关系。无论何种光线，其被材质表面所反射的能量将无法再被材质吸收。因此，诸如折射光这样的余下的进入表面之中的能量正好就是我们计算完反射之后余下的能量。

二：关于辐射度量学

1. 辐射度量学是一种用来度量电磁场辐射（包括可见光）的手段。有很多种辐射度量(radiometric quantities)可以用来测量曲面或者某个方向上的光。
2. 立体角： 立体角用ω表示，它可以为我们描述投射到单位球体上的一个截面的大小或者面积。投射到这个单位球体上的截面的面积就被称为立体角(Solid Angle)，你可以把立体角想象成为一个带有体积的方向。
   • 
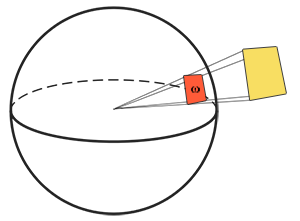
   • 可以把自己想象成为一个站在单位球面的中心的观察者，向着投影的方向看。这个投影轮廓的大小就是立体角。
3. 基本概念：
   • 辐射能量： radiant energy.用Q表示：Q = hv，其中 h 为普朗克常数 6.62620×10−34J · s，v表示频率
   • 辐射通量： radiant flux,用Φ表示：表⽰光源每秒钟发射的功率（dΦ/dt），其单位为⽡特 W。
     • 光是由多种不同波长的能量所集合而成的，而每种波长则与一种特定的（可见的）颜色相关。因此一个光源所放射出来的能量可以被视作这个光源包含的所有各种波长的一个函数。
     • 波长介于390nm到700nm（纳米）的光被认为是处于可见光光谱中，也就是说它们是人眼可见的波长。
     • 辐射通量将会计算这个由不同波长构成的函数的总面积。直接将这种对不同波长的计量作为参数输入计算机图形有一些不切实际，因此我们通常不直接使用波长的强度而是使用三原色编码，也就是RGB（或者按通常的称呼：光色）来作为辐射通量表示的简化。这套编码确实会带来一些信息上的损失，但是这对于视觉效果上的影响基本可以忽略。
   • 辐射强度： radiant intensity,用I表示；I 也是⼀个与距离⽆关的量.
     • 在不同的⽅向上具有不同辐射强度。
     • 辐射强度(Radiant Intensity)表示的是在单位球面上，一个光源向每单位立体角所投送的辐射通量。
     • 举例来说，假设一个全向光源向所有方向均匀的辐射能量，辐射强度就能帮我们计算出它在一个单位面积（立体角）内的能量大小：
     • 
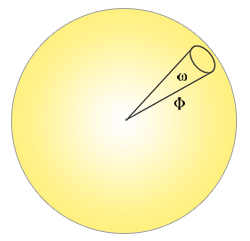
     • 计算辐射强度的公式如下所示：\(I = \frac{d\Phi}{d\omega}\)。其中I表示辐射通量Φ除以立体角ω。
   • 辐射亮度：（也叫辐射率） radiance,用L表示；表⽰的是某个点在某个⽅向上的亮度，在计算机图形学中它是⼀束光的亮度，
     • 是光照⽅程最终要计算量。且L 的值不随距离发射点距离的变化⽽变化。
     • 一个拥有辐射强度Φ的光源在单位面积A，单位立体角ω上的辐射出的总能量(辐射率方程)：\(L=\frac{d^2\Phi}{ dA d\omega \cos\theta}\)
     • 
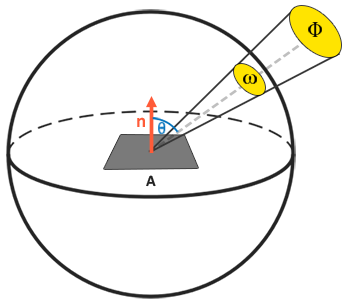
     • 辐射率是辐射度量学上表示一个区域平面上光线总量的物理量，它受到入射(Incident)（或者来射）光线与平面法线间的夹角θ的余弦值cosθ的影响：当直接辐射到平面上的程度越低时，光线就越弱，而当光线完全垂直于平面时强度最高。
     • 其中cosθ就直接对应于光线的方向向量和平面法向量的点积.
     • 辐射率方程很有用，因为它把大部分我们感兴趣的物理量都包含了进去。如果我们把立体角ω和面积A看作是无穷小的，那么我们就能用辐射率来表示单束光线穿过空间中的一个点的通量。
     • 这就使我们可以计算得出作用于单个（片段）点上的单束光线的辐射率，我们实际上把立体角ω转变为方向向量ω然后把面A转换为点p。这样我们就能直接在我们的着色器中使用辐射率来计算单束光线对每个片段的作用了。
   • 辐射照度（辐照度）： irradiance,用E表示；它是点 (ξ, η) 沿各个⽅向对辐射亮度 L 的积分。
     • ⼀个⾯上某点接收来⾃各个⽅向的辐射亮度形成辐射照度。
     • 事实上，当涉及到辐射率时，我们通常关心的是所有投射到点p上的光线的总和，而这个和就称为辐射照度或者辐照度(Irradiance)。

二： 关于反射率方程：

1. \(L_o(p,\omega_o) = \int\limits_{\Omega} f_r(p,\omega_i,\omega_o) L_i(p,\omega_i) n \cdot \omega_i d\omega_i\)
2. 我们知道在渲染方程中L代表通过某个无限小的立体角ωi在某个点上的辐射率，而立体角可以视作是入射方向向量ωi。
3. 注意我们利用光线和平面间的入射角的余弦值cosθ来计算能量，亦即从辐射率公式L转化至反射率公式时的n⋅ωi。
4. 用ωo表示观察方向，也就是出射方向，反射率公式计算了点p在ωo方向上被反射出来的辐射率Lo(p,ωo)的总和。或者换句话说：Lo表示了从ωo方向上观察，光线投射到点p上反射出来的辐照度。
5. 基于反射率公式是围绕所有入射辐射率的总和，也就是辐照度来计算的，所以我们需要计算的就不只是是单一的一个方向上的入射光，而是一个以点p为球心的半球领域Ω内所有方向上的入射光。
6. 一个半球领域(Hemisphere)可以描述为以平面法线n为轴所环绕的半个球体：
7. 为了计算某些面积的值，或者像是在半球领域的问题中计算某一个体积的时候我们会需要用到一种称为积分(Integral)的数学手段，也就是反射率公式中的符号∫，它的运算包含了半球领域Ω内所有入射方向上的dωi 。
8. 积分运算的值等于一个函数曲线的面积，它的计算结果要么是解析解要么就是数值解。由于渲染方程和反射率方程都没有解析解，我们将会用离散的方法来求得这个积分的数值解。
9. 这个问题就转化为，在半球领域Ω中按一定的步长将反射率方程分散求解，然后再按照步长大小将所得到的结果平均化。这种方法被称为黎曼和(Riemann sum) 。

int steps = 100;
float sum = 0.0f;
vec3 P    = ...;
vec3 Wo   = ...;
vec3 N    = ...;
float dW  = 1.0f / steps;
for(int i = 0; i < steps; ++i)
{
    vec3 Wi = getNextIncomingLightDir(i);
    sum += Fr(p, Wi, Wo) * L(p, Wi) * dot(N, Wi) * dW;
}

1. 通过利用dW来对所有离散部分进行缩放，其和最后就等于积分函数的总面积或者总体积。这个用来对每个离散步长进行缩放的dW可以认为就是反射率方程中的dωi 。在数学上，用来计算积分的dωi 表示的是一个连续的符号，而我们使用的dW在代码中和它并没有直接的联系（因为它代表的是黎曼和中的离散步长），这样说是为了可以帮助你理解。
2. 请牢记，使用离散步长得到的是函数总面积的一个近似值。细心的读者可能已经注意到了，我们可以通过增加离散部分的数量来提高黎曼和的准确度(Accuracy)。
3. 反射率方程概括了在半球领域Ω内，碰撞到了点p上的所有入射方向ωi 上的光线的辐射率，并受到fr的约束，然后返回观察方向上反射光的Lo。
4. 正如我们所熟悉的那样，入射光辐射率可以由光源处获得，此外还可以利用一个环境贴图来测算所有入射方向上的辐射率，我们将在未来的IBL教程中讨论这个方法。
5. 现在唯一剩下的未知符号就是fr(也叫做S)了，它被称为BRDF，或者双向反射分布函数(Bidirectional Reflective Distribution Function) ，它的作用是基于表面材质属性来对入射辐射率进行缩放或者加权。

三：关于双向反射分布函数（BRDF）：

1. 函数由2个⽅向组成，具有4个变量，它本质上指明了每个⽅向的⼊射光在各个⽅向上的反射光分布。
2. BRDF，或者说双向反射分布函数，它接受入射（光）方向ωi，出射（观察）方向ωo，平面法线n以及一个用来表示微平面粗糙程度的参数a作为函数的输入参数。BRDF可以近似的求出每束光线对一个给定了材质属性的平面上最终反射出来的光线所作出的贡献程度。
3. 举例来说，如果一个平面拥有完全光滑的表面（比如镜面），那么对于所有的入射光线ωi（除了一束以外）而言BRDF函数都会返回0.0 ，只有一束与出射光线ωo拥有相同（被反射）角度的光线会得到1.0这个返回值。
4. BRDF基于我们之前所探讨过的微平面理论来近似的求得材质的反射与折射属性。对于一个BRDF，为了实现物理学上的可信度，它必须遵守能量守恒定律，也就是说反射光线的总和永远不能超过入射光线的总量。严格上来说，同样采用ωi和ωo作为输入参数的 Blinn-Phong光照模型也被认为是一个BRDF。然而由于Blinn-Phong模型并没有遵循能量守恒定律，因此它不被认为是基于物理的渲染。
5. 现在已经有很好几种BRDF都能近似的得出物体表面对于光的反应，但是几乎所有实时渲染管线使用的都是一种被称为Cook-Torrance BRDF模型。Cook-Torrance BRDF兼有漫反射和镜面反射两个部分：\(f_r = k_d f_{lambert} + k_s f_{cook-torrance}\)
6. 这里的kd是早先提到过的入射光线中被折射部分的能量所占的比率，而ks是被反射部分的比率。BRDF的左侧表示的是漫反射部分，这里用flambert来表示。它被称为Lambertian漫反射，这和我们之前在漫反射着色中使用的常数因子类似，用如下的公式来表示：\(f_{lambert} = \frac{c}{\pi}\)
7. c 表示表面颜色（回想一下漫反射表面纹理）。除以π是为了对漫反射光进行标准化，因为前面含有BRDF的积分方程是受π影响的（我们会在IBL的教程中探讨这个问题的）。
8. 这个Lambertian漫反射和我们之前经常使用的漫反射到底有什么关系：之前我们是用表面法向量与光照方向向量进行点乘，然后再将结果与平面颜色相乘得到漫反射参数。点乘依然还在，但是却不在BRDF之内，而是转变成为了Lo积分末公式末尾处的n⋅ωi 。
9. BRDF的镜面反射部分要稍微更高级一些，它的形式如下所示：\(f_{cook-torrance} = \frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)}\)
10. Cook-Torrance BRDF的镜面反射部分包含三个函数，此外分母部分还有一个标准化因子 。字母D，F与G分别代表着一种类型的函数，各个函数分别用来近似的计算出表面反射特性的一个特定部分。三个函数分别为正态分布函数(Normal Distribution Function)，菲涅尔方程(Fresnel Rquation)和几何函数(Geometry Function).
    
    * 正态分布函数：估算在受到表面粗糙度的影响下，取向方向与中间向量一致的微平面的数量。这是用来估算微平面的主要函数。
    
    * 几何函数：描述了微平面自成阴影的属性。当一个平面相对比较粗糙的时候，平面表面上的微平面有可能挡住其他的微平面从而减少表面所反射的光线。
    
    * 菲涅尔方程：菲涅尔方程描述的是在不同的表面角下表面所反射的光线所占的比率。
11. 以上的每一种函数都是用来估算相应的物理参数的，而且你会发现用来实现相应物理机制的每种函数都有不止一种形式。它们有的非常真实，有的则性能高效。你可以按照自己的需求任意选择自己想要的函数的实现方法。

四： 正态分布函数

五： 几何函数

六： 菲涅尔方程

七： Cook-Torrance反射率方程

1. 随着Cook-Torrance BRDF中所有元素都介绍完毕，我们现在可以将基于物理的BRDF纳入到最终的反射率方程当中去了：\(L_o(p,\omega_o) = \int\limits_{\Omega} (k_d\frac{c}{\pi} + k_s\frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)})L_i(p,\omega_i) n \cdot \omega_i d\omega_i\)
2. 这个方程现在完整的描述了一个基于物理的渲染模型，它现在可以认为就是我们一般意义上理解的基于物理的渲染也就是PBR。