理解图像Garbor和HOG特征的提取方法及实例应用

前言：今天接触到了这两个特征，看了课本和博客后很蒙蔽，没有理解这两个特征，本篇博客的目的是只是参考其他的博客总结这两个特征，如果未来能研究和工作领域是这方面的话再回来自己研学，如有错误也欢迎指出。

Garbor特征

一.Gabor 特征的简介

Gabor 特征是一种可以用来描述图像纹理信息的特征，Gabor 滤波器的频率和方向与人类的视觉系统类似，特别适合于纹理表示与判别。Gabor 特征主要依靠 Gabor 核在频率域上对信号进行加窗，从而能描述信号的局部频率信息。

说到 Gabor 核，不能不提到傅里叶变换。正是靠傅里叶变换，我们才能将信号转换到频率域，才能让Gabor核在频率域去加窗。而在原本的空间域中，一个 Gabor 核实际上就是一个高斯核与正弦波调制的结果。

如下图所示，分别为正弦函数，高斯函数，调和后的函数。通过频率参数和高斯函数参数的选取，Gabor变换可以选取很多纹理特征，但是Gabor是非正交的，不同特征分量之间有冗余。

 

二.Gabor核及其变换

如果从Fourier变换的角度来看，Gobor变换就是窗函数取高斯窗时的短时Fourier变换。

 

 

三.Gabor特征提取

先对图像I(x,y)进行实数形式的Gabor变换，得到处理后的图像，直接提取特征的话，特征维数太高，不利于后续处理。一般对图像分块，例如：分别水平和垂直方向取16等分，将整个图像分成64个16x16大小的子图像块。

然后计算每一块对应的能量。

 

计算之后得到联合空间频率能量矩阵Energy。最后将能量矩阵降维成1x64的行向量，作为原始图像在某一方向和尺度变换后的特征向量。

HOG特征

1.算法基本流程

　　在一幅图像中，方向梯度直方图（Histogram of Oriented Gradient, HOG）能够很好地描述局部目标区域的特征，是一种常用的特征提取方法，HOG+SVM在行人检测中有着优异的效果。在HOG中，对一幅图像进行了如下划分： 
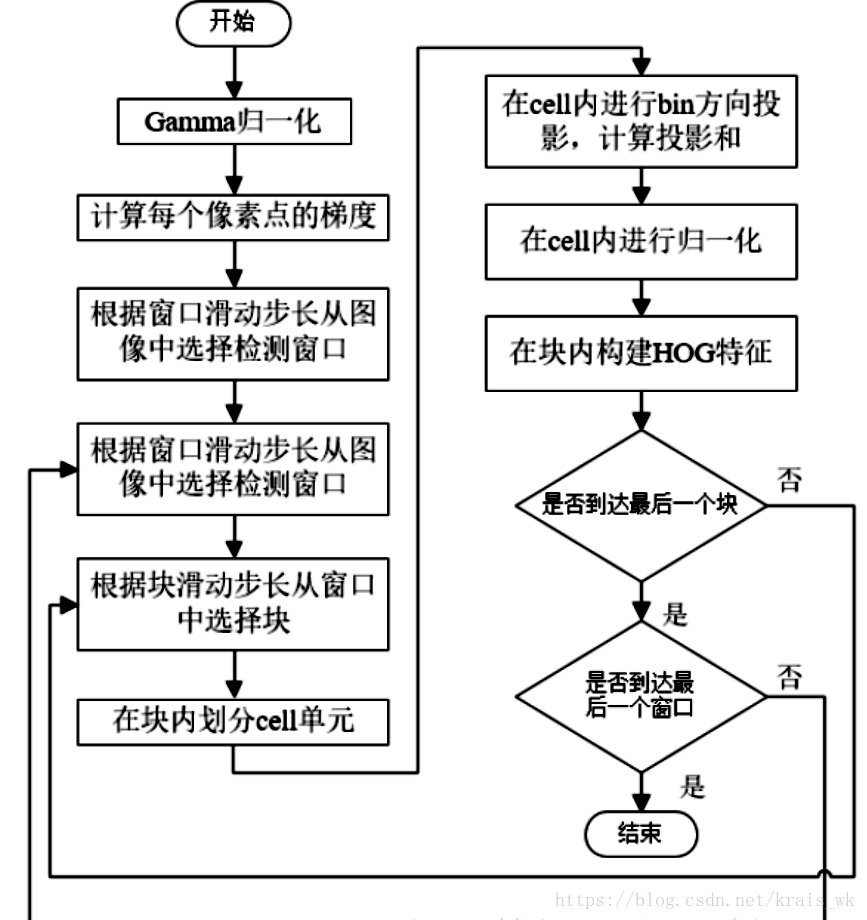
图像(image)->检测窗口(win)->图像块(block)->细胞单元(cells)
流程图如下：  

2.计算图像梯度

　　对数字图像而言，每个像素水平和垂直方向的梯度，可以通过下图的kernels计算：
　　

　　即可写为：
　　

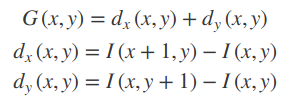
　　每个像素梯度大小和方向可表示为：
　　

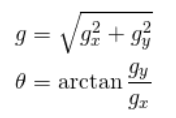
　　其中，I(x,y)是图像在点(x,y)处的像素值。
　　梯度图像移除了不必要的信息，但是高亮了轮廓线。在每一个像素上，梯度都有大小和方向。对于彩色图像，3个通道的梯度都将被计算出来，然而图像素的梯度值为3个通道中最大的梯度值，角度也是最大角度。

 

3.HOG的win ,block ,cell

 

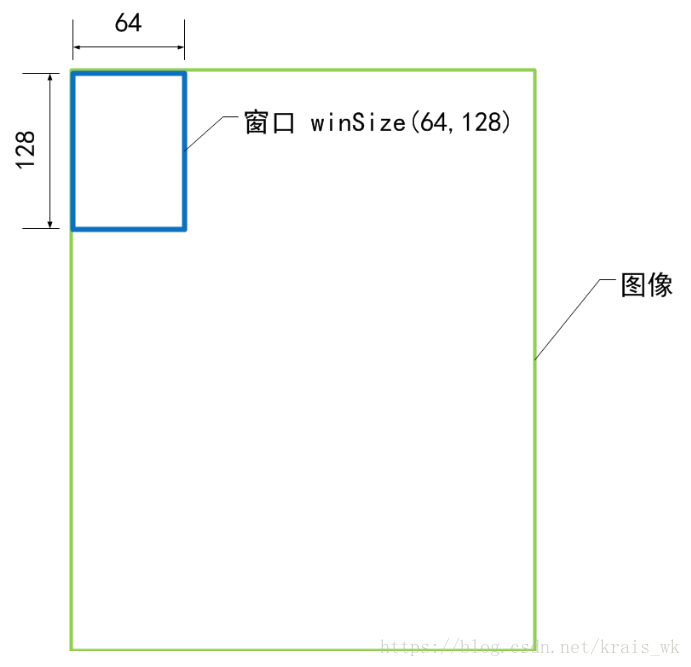
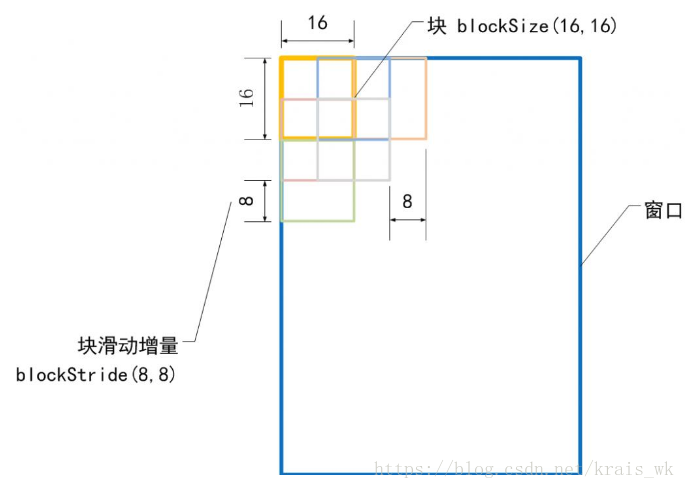
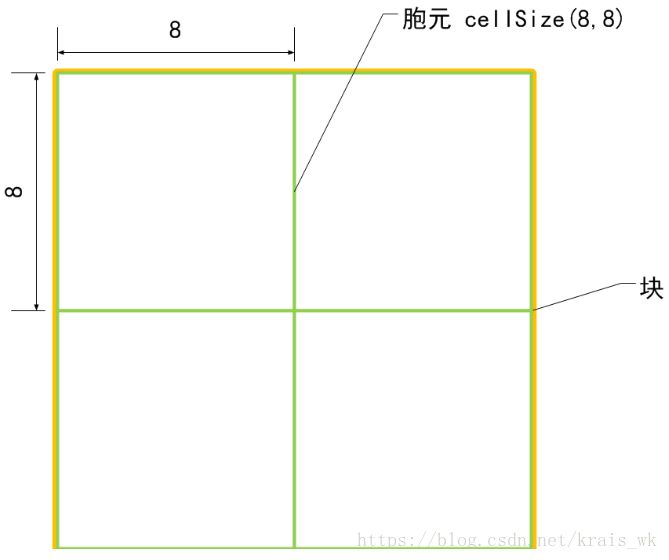
　　对于图像中检测窗口的尺寸为64×64，假设给出块的尺寸为16×16，块步长为(8,8)，经过计算：检测窗口中共滑动7×7=49个block。在一个块中选择细胞单元不再滑动，给出细胞单元的尺寸为(8,8)，所以一个块中一共有2×2=4个cell。

4.HOG构建方向梯度直方图与特征向量维数

　　HOG构建方向梯度直方图在cell中完成，bins的个数决定了方向的范围。假设采用9个bin的直方图来统计这8×8个像素cell的梯度信息，即将cell的梯度方向0～180度（或0～360度，考虑了正负，signed）分成9个方向块。如下图所示：如果这个像素的梯度方向是20-40度，直方图第2个bin即的计数就加1，这样，对cell内每个像素用梯度方向在直方图中进行加权投影，将其映射到对应的角度范围块内，就可以得到这个cell的梯度方向直方图了，就是该cell对应的9维特征向量（因为有9个bin）。这边的加权投影所用的权值为当前点的梯度幅值。例如说：某个像素的梯度方向是20-40度，其梯度幅值是4，那么直方图第2个bin的计数就不是加1了，而是加4。这样就得到关于梯度方向的一个加权直方图。之前提到过，cell的中方向范围的个数由bins来决定，还是以9为例：所以，一个cell中的向量为9个。以上面的例子，在一个尺寸为64×64的检测窗中，描述子的维数就应该为：9×4×49=1764 。其中4为一个block中cell的个数，49为一个win中block的个数。