JAVA数据结构--二叉查找树

二叉查找树定义

二叉查找树（英语：Binary Search Tree），也称二叉搜索树、有序二叉树（英语：ordered binary tree），排序二叉树（英语：sorted binary tree），是指一棵空树或者具有下列性质的二叉树：

1. 若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
2. 若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
3. 任意节点的左、右子树也分别为二叉查找树；
4. 没有键值相等的节点。

二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低。为O(log n)。

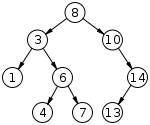三层二叉查找树

二叉查找树的操作主要是运用的递归的思想，可操作的Object类必须继承了Comparable接口，个人实现查找树主要是参考了《数据结构与算法分析》这本书。因为遍历涉及到三种遍历方式，所以届时单独开一篇。

树的结点定义

 private static class BinaryNode<T>{
         BinaryNode(T theElement) {
             this(theElement,null,null);
         }
         BinaryNode(T theElement,BinaryNode<T> lt,BinaryNode<T> rt) {
             element=theElement;
             left=lt;
             right=rt;
         }
         T element;//根节点
         BinaryNode<T> left;//左子树
         BinaryNode<T> right;//右子树
     }

contains方法

 private boolean contains(T x,BinaryNode<T> t){
         if(t==null)
             return false;
         int compareResult=x.compareTo(t.element);
         if(compareResult<0)
             return contains(x,t.left);    //递归
         else if (compareResult>0) {
             return contains(x, t.right);
         }
         else {
             return true;
         }
     }

contains方法主要是查找当前二叉树是否还有某个节点，利用了comparaTo方法递归调用。

findMin()与findMax()方法

 private BinaryNode<T> findMin(BinaryNode<T> t){
         //非递归写法
         if(t!=null)
             while(t.left!=null)
                 t=t.left;
         return t;
         //递归写法
         /*if(t==null)
             return null;
         else if (t.left==null) {
             return t;
         }
         return findMin(t.left);*/
     }

findMin与findMax方法类似，这里只列出一种即可。然后仍有两种方法解决此问题，一种为递归，一种非递归。

非递归方法就是采用了while循坏思想，直到找出最左的节点即可。

insert方法

 private BinaryNode<T> insert(T x,BinaryNode<T> t){
         if(t==null)//生成新的节点
             return new BinaryNode<T>(x, null, null);
         if(contains(x))//如果二叉树中已经有x元素，则不进行任何操作
             return t;
         else {
             int compareResult=x.compareTo(root.element);
             if(compareResult<0){
                 t.left=insert(x, t.left);
             }
             else {
                 t.right=insert(x, t.right);
             }
             return t;
         }
     }

remove方法

 private BinaryNode<T> remove(T x,BinaryNode<T> t){
         if(t==null)
             return t;
         int compareResult=x.compareTo(t.element);
         if(compareResult<0){
             t.left=remove(x, t.left);
         }
         else if(compareResult>0){
             t.right=remove(x, t.right);
         }
         else if (t.left!=null&&t.right!=null) {    //两个孩子情况，采取懒惰删除
             t.element=findMin(t.right).element;
             t.right=remove(t.element, t.right);
         }
         else {    //单个孩子情况
             t=(t.left!=null)?t.left:t.right;
         }
         return t;
     }

删除节点时需要考虑两种情况，一种为两个孩子的情况，一种为单个孩子的情况。

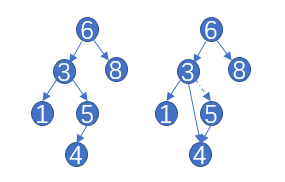如图为删除5节点为单个孩子情况

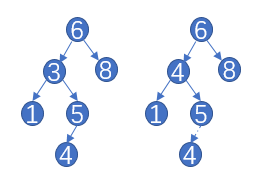此图是删除3节点两个孩子的情况，具体做法是找出该节点右子树中最小的节点替换当前删除的节点

全部的代码如下（暂缺遍历）

 package Tree;

 public class BinarySearchTree<T extends Comparable<? super T>> {
     private static class BinaryNode<T>{
         BinaryNode(T theElement) {
             this(theElement,null,null);
         }
         BinaryNode(T theElement,BinaryNode<T> lt,BinaryNode<T> rt) {
             element=theElement;
             left=lt;
             right=rt;
         }
         T element;//根节点
         BinaryNode<T> left;//左子树
         BinaryNode<T> right;//右子树
     }
     private BinaryNode<T> root;//定义根节点
     public BinarySearchTree() {
         root=null;
     }
     public void makeEmpty(){
         root=null;
     }
     public boolean isEmpty(){
         return root==null;
     }
     public boolean contains(T x){
         return contains(x,root);
     }
     public T findMin() throws Exception{
         if(isEmpty())
             throw new Exception();
         return findMin(root).element;
     }
     public T findMax() throws Exception{
         if(isEmpty())
             throw new Exception();
         return findMax(root).element;
     }
     public void insert(T x){
         root=insert(x,root);
     }
     public void remove(T x){
         root=remove(x,root);
     }
     private boolean contains(T x,BinaryNode<T> t){
         if(t==null)
             return false;
         int compareResult=x.compareTo(t.element);
         if(compareResult<0)
             return contains(x,t.left);    //递归
         else if (compareResult>0) {
             return contains(x, t.right);
         }
         else {
             return true;
         }
     }
     private BinaryNode<T> findMin(BinaryNode<T> t){
         //非递归写法
         if(t!=null)
             while(t.left!=null)
                 t=t.left;
         return t;
         //递归写法
         /*if(t==null)
             return null;
         else if (t.left==null) {
             return t;
         }
         return findMin(t.left);*/
     }
     private BinaryNode<T> findMax(BinaryNode<T> t){
         if(t!=null)
             while(t.right!=null)
                 t=t.right;
         return t;
     }
     private BinaryNode<T> insert(T x,BinaryNode<T> t){
         if(t==null)//生成新的节点
             return new BinaryNode<T>(x, null, null);
         if(contains(x))//如果二叉树中已经有x元素，则不进行任何操作
             return t;
         else {
             int compareResult=x.compareTo(root.element);
             if(compareResult<0){
                 t.left=insert(x, t.left);
             }
             else {
                 t.right=insert(x, t.right);
             }
             return t;
         }
     }
     private BinaryNode<T> remove(T x,BinaryNode<T> t){
         if(t==null)
             return t;
         int compareResult=x.compareTo(t.element);
         if(compareResult<0){
             t.left=remove(x, t.left);
         }
         else if(compareResult>0){
             t.right=remove(x, t.right);
         }
         else if (t.left!=null&&t.right!=null) {    //两个孩子情况，采取懒惰删除
             t.element=findMin(t.right).element;
             t.right=remove(t.element, t.right);
         }
         else {    //单个孩子情况
             t=(t.left!=null)?t.left:t.right;
         }
         return t;
     }

 }

也可访问我的gihub数据结构的部分，暂时内容较少。