【51nod-1138】连续整数的和

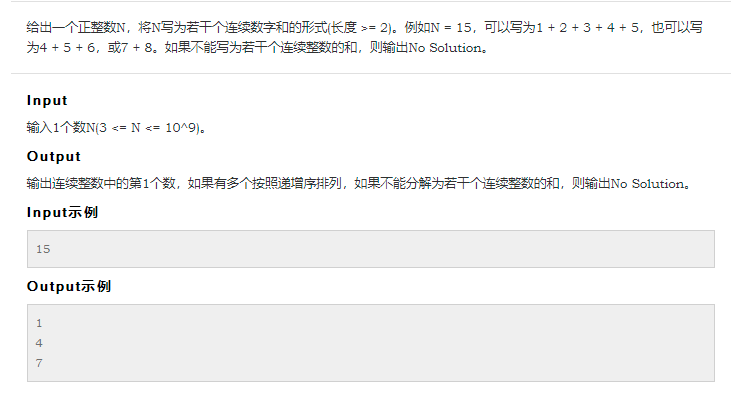
本来想着用尺取的思想，不过会超时。利用等差数列S = na+n*n(n-1)/2,得a = (2*S-n*(n-1))/(2*n),然后遍历n，只要满足a是整数就可以，这样复杂度从O（S）变成了O（sqrt（S））。

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = ;
int a[N];
int main()
{
    int m, c = ;
    cin>>m;
    for(int i=; i*(i-)<*m; i++)
    {
        if((*m-i*(i-))%(*i)==)
            a[c++] = (*m-i*(i-))/(*i);
    }
    sort(a, a+c);
    for(int i=; i<c-; i++)
        printf("%d\n", a[i]);
    if(c==) puts("No Solution");
    return ;
}