1、基础配置

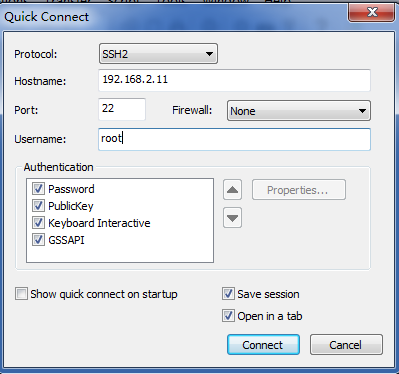
安装SecureCRT 8.0链接到虚拟服务器，并配置docker

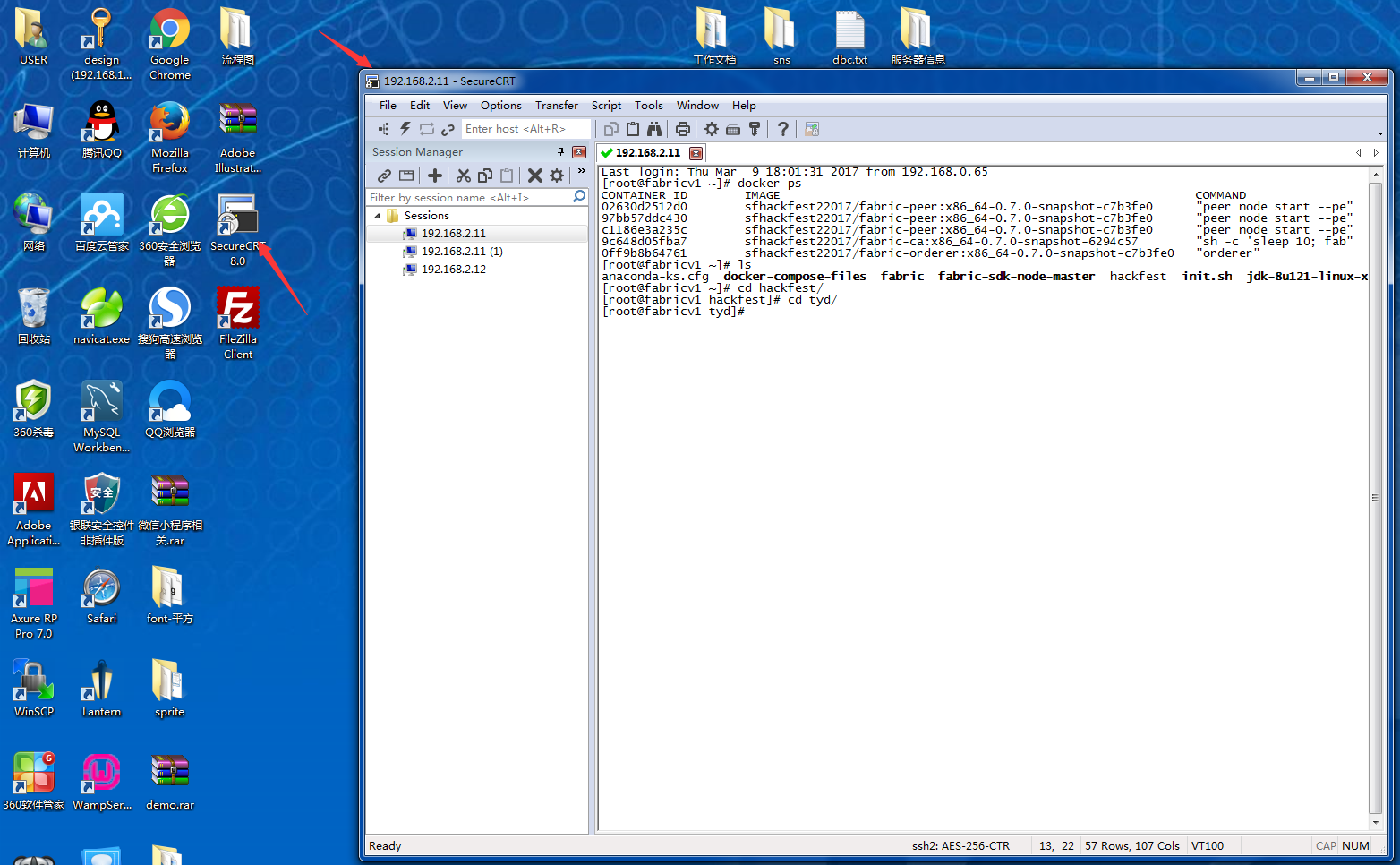
安装文件上传到服务器工具FileZilla

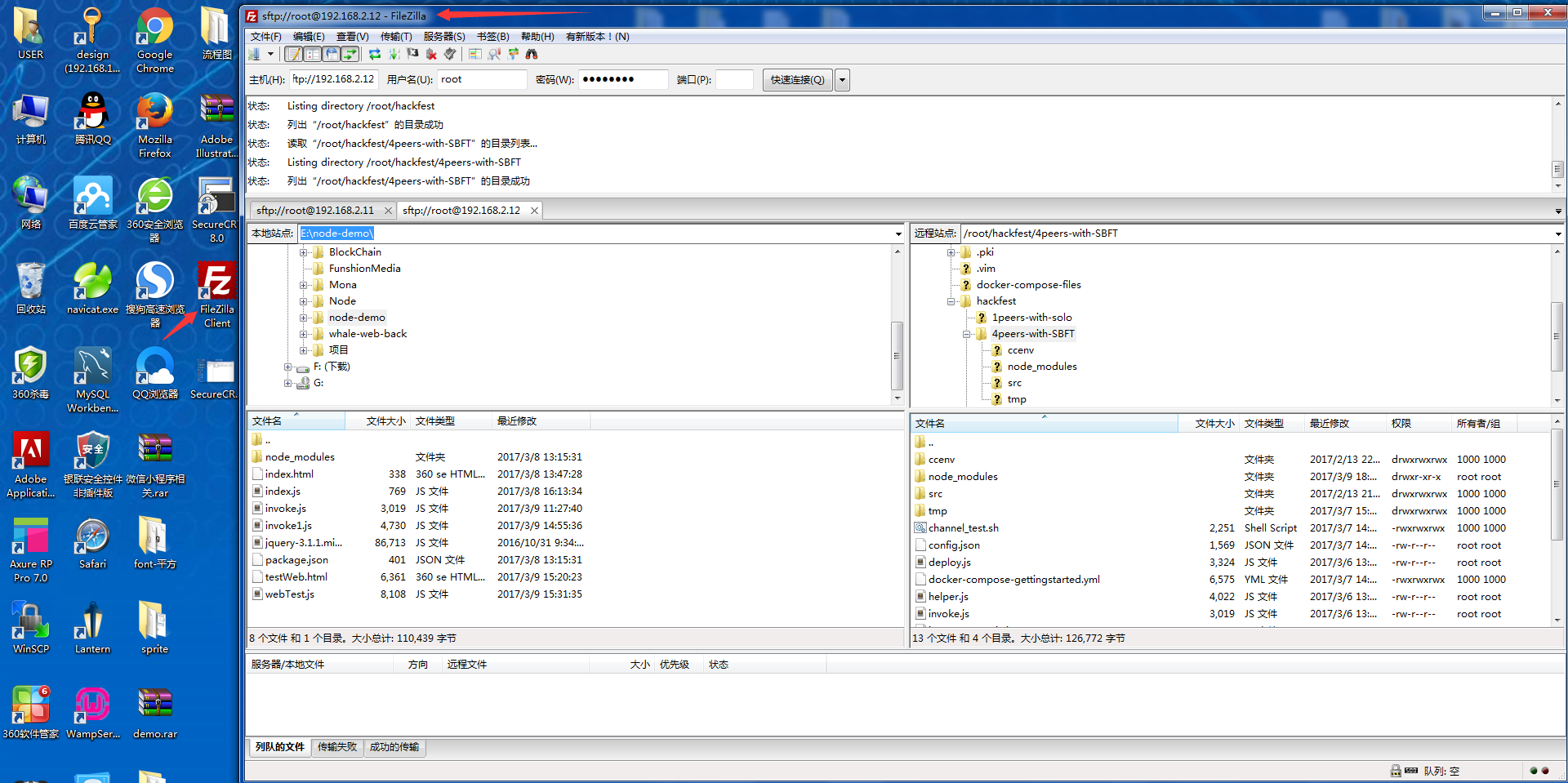
工作笔记——区块链POC的更多相关文章

  1. 开源VS商用，IBM区块链从Hyperledger到商用平台之道 | 对话IBM高级架构师【 笔记】（转）

    https://www.toutiao.com/a6520005731867951619/?tt_from=weixin&utm_campaign=client_share&times ...

  2. Imcash解读：哪些行业的“饭碗”最容易受区块链的影响？

    或许,你已经听到很多人说,区块链是本世纪一项伟大的革命性技术,在未来“前途无量”. 但是,很少有人能真正接地气地举例说清楚:区块链到底怎么革命,革谁的命,怎么产生价值,将会颠覆哪些行业. 今天,我们就 ...

  3. VRF在区块链中的应用

    最近区块链领域流行了一种"怪病",许多区块链项目或者设计方案都加入了一个叫做VRFs的算法.那么, (1) 什么是VRFs? (2) VRFs在区块链中解决了什么问题? 本文旨在介 ...

  4. 区块链入门级别认知（blockchain）

    区块链入门级别认知(blockchain) 前言:今天参加了迅雷关于区块链的大会,学习和感受总结一下 之前的认知在:几个混迹互联网圈关于区块链 耳熟能详的 热词 “比特币” “区块链” “挖矿” ,知 ...

  5. 用Java实现简单的区块链

    用 Java 实现简单的区块链 1. 概述 本文中,我们将学习区块链技术的基本概念.也将根据概念使用 Java 来实现一个基本的应用程序. 进一步,我们将讨论一些先进的概念以及该技术的实际应用. 2. ...

  6. 以太坊区块链Java（EthereumJ）学习笔记：概述

    本系列文章介绍以太坊区块链基于Java语言的解决方案.通过介绍EthereumJ定义的主要模块和Class,希望为大家学习和使用EthereumJ提供一些帮助. 整体架构 以太坊的Java解决方案主要 ...

  7. AbelSu的区块链笔记

    最近几年,像比特币.以太坊.ICO.区块链等概念突然成为互联网热门话题,今天写这篇博客,也是做一些笔记,大概说一下对这个的解释和其他相关内容. 区块链: 区块链是分布式数据存储.点对点传输.共识机制. ...

  8. HyperLedger Fabric 1.4 区块链工作过程（2.3）

    区块链的工作过程分交易产生.交易广播.节点计算.获取记账权.记账权广播.接收区块.验证区块和完成记账七个过程. 1) 交易产生:用户向区块链发了一笔交易信息,将产生交易:2) 交易广播:当一笔新交易产 ...

  9. 《区块链DAPP开发入门、代码实现、场景应用》笔记5——区块链福利彩票的设计

    笔者一直强调,一定要利用区块链的特点来解决行业存在的问题,并且该问题最好用区块链解决或者说只能用区块链解决.彩票行业就是个例子. 在讲解代码之前,首先讲解一下业务设计,如图6.15所示. 图6.15 ...

随机推荐

  1. pycharm Tab键设置成4个空格

    file--->setting,选择Editor--->python,如下图所示:

  2. Service层事务不能回滚的解决方式

    1.在service方法里面如果对异常进行了捕获的话,该事务是不会进行回滚的        默认spring事务只在发生未被捕获的 runtimeexcetpion时才回滚.          spr ...

  3. Spring配置文件总结

    http://blog.csdn.net/zhejingyuan/article/details/41042789

  4. Windows远程桌面没有密码的电脑

    你如果想远程一个密码为空的机器,默认情况下是不可以的,需要进行以下设置 1.windows家庭版不支持远程桌面 2. 3.搜索“本地安全策略”

  5. php 实现Iterator 接口

    <?php class MyIterator implements Iterator{ private $var = array(); public function __construct($ ...

  6. CentOS 6.5 配置IP地址的三种方法

    1.自动获取IP地址虚拟机使用桥接模式,相当于连接到物理机的网络里,物理机网络有DHCP服务器自动分配IP地址.#dhclient 自动获取ip地址命令#ifconfig 查询系统里网卡信息,ip地址 ...

  7. oracle的between用来判断时间区间

    SELECT * FROM warning_form wfwhere wf.start_time between trunc(sysdate,'mm') and sysdate; start_time ...

  8. 1：TwoSum(如果两个和为某个数，找出这俩数的位置)

    package leetcode; import java.util.HashMap; import java.util.Map; /** * @author mercy *Example: *Giv ...

  9. Java调用http保留访问状态

    package com.coracle; import com.coracle.yk.xframework.util.yunTongXun.HttpRequest; import java.io.*; ...

  10. libtorch 哪些函数比较常用？

    libtorch 加载 pytorch 模块进行预测示例 void mat2tensor(const char * path, torch::Tensor &output) { //读取图片 ...