计量经济与时间序列_关于Box-Jenkins的ARMA模型的经济学意义(重要思路)

1　　很多人已经了解到AR(1)这种最简单的时间序列模型，ARMA模型包括AR模型和MA模型两个部分，这里要详细介绍Box-Jenkins模型的观念(有些资料中把ARMA模型叫做Box-Jenkins模型，都是一会儿事，这里说明一下)，并说明模型。

2　　首先现将重点放在介绍“单变数时间序列模型”(univariate time series model)，也就是从模型中只有“一个”时间序列变数来开始谈起，但你必须先要记住的是其实时间模型也可以包含“多变数”的情况。

3　　什么是Box-Jenkins模型？

　　这是两个人，Jenkins应该是威尔士人，Box先生应该是英国人，不过两位先生已经仙逝了。在网上只能找到Box的照片，具体的资料可以参考维基的这个链接，有这两个人的详细介绍。

　　https://en.wikipedia.org/wiki/George_E._P._Box

　　https://en.wikipedia.org/wiki/Gwilym_Jenkins

　　

　　　　　　　　　　(George Box)

　　模型查到的资料是从1976年开始发展的。ARMA模型的前提假设是时间序列资料必须是定态(stationary，当然大多数教材叫稳定性，还有稳定性检测，或者叫稳态，都一会儿事儿。然后又再次进出时发明了ARIMA模型。如果你要疑问什么是stationary？一会儿会谈到。另外，这篇文，希望大多数人把它当做一个哲学文来阅读。

4　　白噪音(白噪声，white noise)

　　(1)　　很多时候有些概念译名都不太一样，所以多了解一些这方面的东西，不要引起歧义。虽然这个名词有点儿怪怪的，其实想表达的意思不是白的？也不是噪声？不知道为啥会这么翻译。在baidu中搜索这个名词，在物理学里面有这个解释，是关于声音的，解释如下：“白噪音是指一段声音中的频率分量的功率在整个可听范围（0～20KHZ）内都是均匀的。由于人耳对高频敏感，这种声音听上去是很吵耳的沙沙声。”真不知道跟这个时间序列有啥关系，另外还有很多概念，比如自由度(统计学也用这个概念)，其实这个概念在物理学里面。我们这样理解一下吧：“白噪声就是满足一些“特定统计定义”的时间序列“随机变数”。简单地说，如果有一个时间序列变数以符号ε_t来表示，有的是用μ_t，这个注意一下就可以。

　　(2)　　我从网上找的了白噪声的一张图。

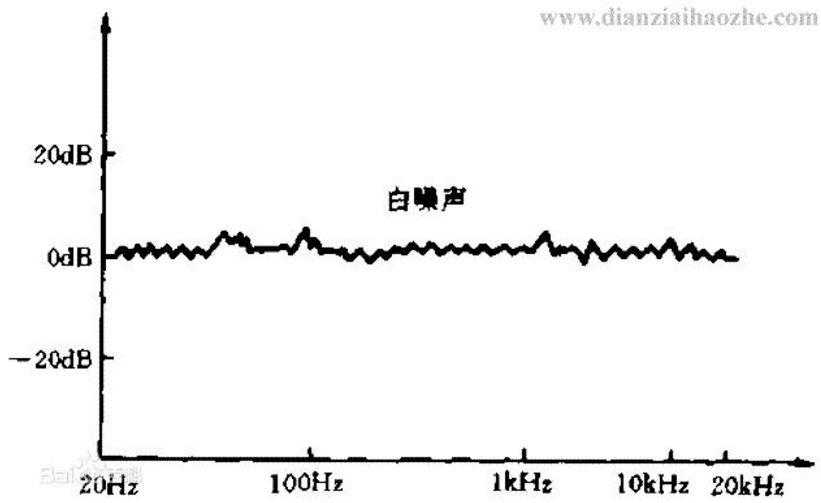
　　这样就容易理解了，我们在学习ARMA模型的时候，所需要的序列是不是假设也是这种的？好吧就用这个white noise这个概念吧。跟这个样一样的东西。

　　(3)　　另外，我们给白噪声下三个定义：

　　第一：期望为0；

　　第二：变异数未固定常数(方差为常数)；

　　第三：自我共变数(autocovariance,也就是自协方差)也等于0。

　　符合这三个条件的时间序列就叫做白噪声，这就是我们找这样的序列，才能建立我们的模型。当然这种东西有点儿难度，世界上哪有这么好的序列？这个先不要管，后面我们慢慢改变这个序列的结构等方式可以基本构建这么一种时间序列，变形金刚可以变形的，另外，科学家和科学的特点就是准确，但是事件万物都是复杂的，怎么能用简单的公式来表示事件万物呢？简单：假设嘛。再就是有些难以预测的东西，很难解释的东西就是有个东西叫残差或者误差，把这个部分做一个加法不就等于一个完整的能表示万物的公式了！当然，我们衡量一个公式(叫模型也行，都一会儿事儿)最简单的一个标准就是：残差或者误差越小越好，模型在未来预测的过程中也是相对越小越好，那么这样你就基本可以跟上帝对话了。

5　　ARMA(p,q)模型。可以劈开两部分，这个就不用说了，学过的都知道。另外这个模型前面有一个常数项，当然有人叫截距项，这个概念和线性回归是一样的。大多数情况下这个截距项可以不要。因为我们在分析模型的平稳性啦，检测单位根等等这个乱七八糟东西，都是在看参数的情况。这个截距项我们根据前面的假设来讲，是iid。这个部分不说太多，p什么样，q什么样变成什么，滞后期就是慢几步的序列，这部分可以参照博客的其他内容都有讲解这个很简单。

6　　摘出来MA，单独讲讲这个部分。我们知道AR模型的经济含义其实不过就是某一个时间序列的经济变数，在结合某些经济假设之后，就会使该变数当期的值会和变数过去的值有某种关联性，所以当期的变数(yt)才会设定成是改变数过去的变数值(也叫滞后期，如yt-1)函数。那也许你很有兴趣知道，什么情况会让现在的yt和过去的ε_t-1相关呢？

　　(1)　　当然MA模型背后也有像AR模型类似的经济意义，只不过一般的计量书籍都直接将之视为理所当然，而不加以说明。很多初学者的误解，认为ARMA模型灭有什么经济理论基础的不正确观念，进而忽视时间序列分析方法的价值，只把它当做没有什么理论的数字或同级游戏。所以这里要加以说明。

　　(2)　　简单说，MA模型隐含这么一个观念——经济行为体系的结构式中，含有误差修正的特性。这个特性特别重要，让我们记住它！

　　(3)　　有何经济含义呢？借用较为熟悉的蛛网理论模型来解释是最方便的了，但我们要给供给函数的设定上加入随机变数ε_t来说明会比较容易懂。在供给函数中加入随机变数，表示生产者供给量的决策仍然不是百分比掌握了，就有误差存在啦。这里的蛛网理论模型就是变成一些三个等式：

　　需求函数：D(Q_t) = α₀ - α₁p_t

　　供给函数：S(Q_t) = β₀ + β₁p_t* + ε_t

　　市场均衡条件：D(Q_t) = S(Q_t)

　　如果你的记忆力不差，能接的上面这组结构式，其实关键性的问题在于生产者对于逾期价格pt*是如何形成的。没错，我们假设了生产者以上一期的价格“推想”当期的价格pt* = pt-1*，所以才能导出在缩减式中价格变数出现了AR(1)的情况。

　　(4)　　现在要做的就是导出所减式具有MA(1)的性质。在这里我们先做一个看起来也行不怎么有说服力的经济假设，即“生产者利用上一次生产时的失误(经验)，加上某一权数考量后，来预期下一期的价格”。先不论你是否同意这样的假设，我们将这个假设用具体的函数式表示出来。如下：

　　　　　　p_t* = h₀ + ε_t-1

　　　　　　其中，h0表示权数大小的常数项，et-1表示上一期生产时发生的失误，这样的模型设定，其实遗憾了所谓误差修正的意义。我们将这个式子带入到上面的可以看一下。等于：p_t = α₀ + ε_t  + b₁ ε_t-1

　　　　　　很有趣吧！显然，上式看起来就是有常数项的MA模型。

　　(5)　　不过，不知道发现没有，这样对价格预期形成的假设是由缺陷的。具体说，因为如果恰巧上一次生产决策预测很早，式预期失误如果为0的话，那么就会使预期价格等于0！！如此一来，这个假设就不符合市场实际可能发生的情况，也就是说这样的假设不尽合理，那么没有比较合理的预测模型呢？在计量文献上有所谓的“适应性预期模型”(Kmenta提出的1986年)，我们只要借用适应性预期模型观念改写成：

　　p_t* = p_t-1*  + h₀ε_t-1

　　那这个对价格预期形成的假设，就变成较为合理的适应性预期模型。

　　(6)　　AR和MA模型的缺陷用这种适应性模型是不是可以更为合理的估计，这个式子是不是很像.....，对！就是ARMA模型。

　　(7)　　哲学点儿讲其中ε_t-1就很像老子的“道”，因为不可测，但是它又发挥自己的作用；只考虑到“道”也不行，我们还要考虑p_t-1，这现实因素，就像孔子的“仁”，出世的东西+入世的东西这才是考虑的比较全面的。

7　　定态与安定条件。

　　(1)　　正如我们学哲学当中有一条叫：变化是绝对的，不变是相对的。在ARMA模型中，也包含这方面的因素。我们在检测模型的stationary的时候要有一个东西叫单位根检测。在Eviews软件中我们可以调出这么一张图来。

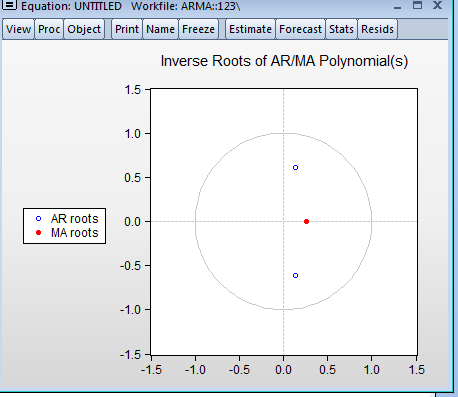
　　在这张图中我们发现没有，像不像打靶的靶子。当然是，这个玩意儿叫单位根检测，咱不管它具体检测方式。如果在靶心当中是安定stationary，靶心外的化就是non-statinary，这就懂了吧。你建立的这个模型好不好。就要看是不是现在在靶心内，还是靶心外。如果样本内建立模型是在靶心内，在样本外去预测的话，他的效果肯定是准确度更大的，这个方面可以通过统计概率统计的，这个问题不在此展开讨论了。

8　　总结：　

　　ARMA模型也叫经济学家的良心。很多资料上面也是这么说的。

　　(1)　　我们不光要考虑可度量的部分的变化也要考虑不可度量部分的变化，这就是ARMA的全面。

　　(2)　　未来我们不知道，通过概率的角度来讲我们不是去预测下刻是对是错，我们只需要知道，在n个以后的每一期预测属不属于在整个大的高概率范围之内，如果是，那么你做10次，错1次，对9次，如果都是等分进行投资，你的胜率是大于90%的。当然概率学就是从研究赌博来的，赌博我们也要科学的赌博，找到这块儿痒痒肉！我们使劲挠，这就是很爽！

　　(3)　　当然，这个ARMA也有缺陷，比如稳定性或者说稳态的持续性能有多长？当偏差过大的时候如何去修正，那就衍生了其他的模型。ARCH模型族就是一个分支。这个模型也是非常好的模型。

　　(4)　　我们在研究一个东西的时候必须就一个经典的模型研究透，研究深入，只有更深更深再深的了解，了解到他的哲学层面才能有更深的应用。而不是知之皮毛，用而弃置！