sklearn中的多项式回归算法
sklearn中的多项式回归算法
1、多项式回归法
多项式回归的思路和线性回归的思路以及优化算法是一致的,它是在线性回归的基础上在原来的数据集维度特征上增加一些另外的多项式特征,使得原始数据集的维度增加,然后基于升维后的数据集用线性回归的思路进行求解,从而得到相应的预测结果和各项的系数。
2、多项式回归的函数在pyhton的sklearn机器学习库中没有专门的定义,因为它只是线性回归方式的一种特例,但是我们自己可以按照多元线性回归的方式对整个过程进行相关的定义,然后包装成为一个函数进行相关的调用即可。
3、对于多项式回归方式的实现过程有以下两种:
(1)原理实现的过程代码(以一元二次函数的拟合为例):
import numpy as np
import matplotlib.pyplot as plt
x=np.random.uniform(-3,3,size=100)
X=x.reshape(-1,1)
y=0.5*x**2+x+2+np.random.normal(0,1,size=100)
plt.figure()
plt.scatter(x,y)
from sklearn.linear_model import LinearRegression
l1=LinearRegression()
l1.fit(X,y)
y_p=l1.predict(X)
plt.plot(X,y_p,"r")
print(l1.score(X,y))
###1-1多项式回归的思路(使用线性回归的的思路,添加新的特征即可,即原数据集的维数增加)
print((x**2).shape)
x2=np.hstack([X,X**2])
print(x2.shape)
L2=LinearRegression()
L2.fit(x2,y)
y_p2=L2.predict(x2)
plt.figure()
plt.scatter(x,y)
plt.plot(X,y_p,"g")
plt.plot(np.sort(x),y_p2[np.argsort(x)],"r") #输出多维数据时的拟合结果
plt.show()
print(L2.score(x2,y))
print(L2.coef_,L2.intercept_)
(2)sklearn中的整体实现过程:
#sklearn中的多项式回归和pipeline
import numpy as np
import matplotlib.pyplot as plt
x=np.random.uniform(-3,3,size=100)
X=x.reshape(-1,1)
y=0.5*x**2+x+2+np.random.normal(0,1,size=100)
from sklearn.preprocessing import PolynomialFeatures
p1=PolynomialFeatures(degree=2) #degree的含义是多项式数据中添加特征的最高次数
p1.fit(X)
x3=p1.transform(X)
print(x3.shape)
print(x3[:5,0])
print(x3[:5,1])
print(x3[:5,2])
print(x3[:5,])
from sklearn.linear_model import LinearRegression
l3=LinearRegression()
l3.fit(x3,y)
y_p3=l3.predict(x3)
plt.figure()
plt.scatter(x,y)
plt.plot(np.sort(x),y_p3[np.argsort(x)],"r")
plt.show()
print(l3.score(x3,y))
print(l3.coef_,L2.intercept_)
print(x3.shape)
(3)利用上述原理进行函数的自我封装调用代码:
#自己封装一个多项式回归的函数
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
def polynomialRegression(degree):
return Pipeline([("poly",PolynomialFeatures(degree=degree)),
("std_scaler",StandardScaler()),
( "lin_reg",LinearRegression())
])
poly2_reg=polynomialRegression(10)
poly2_reg.fit(X,y)
y2=poly2_reg.predict(X)
print(mean_squared_error(y,y2))
print(poly2_reg.score(X,y))
plt.figure()
plt.scatter(X,y)
plt.plot(np.sort(x),y2[np.argsort(x)],"r")
plt.show()
x1=np.linspace(-3,3,100).reshape(100,1)
y11=poly2_reg.predict(x1)
plt.plot(x1,y11,"r")
#plt.axis([-3,3,-1,10])
plt.show()
运行结果如下所示:
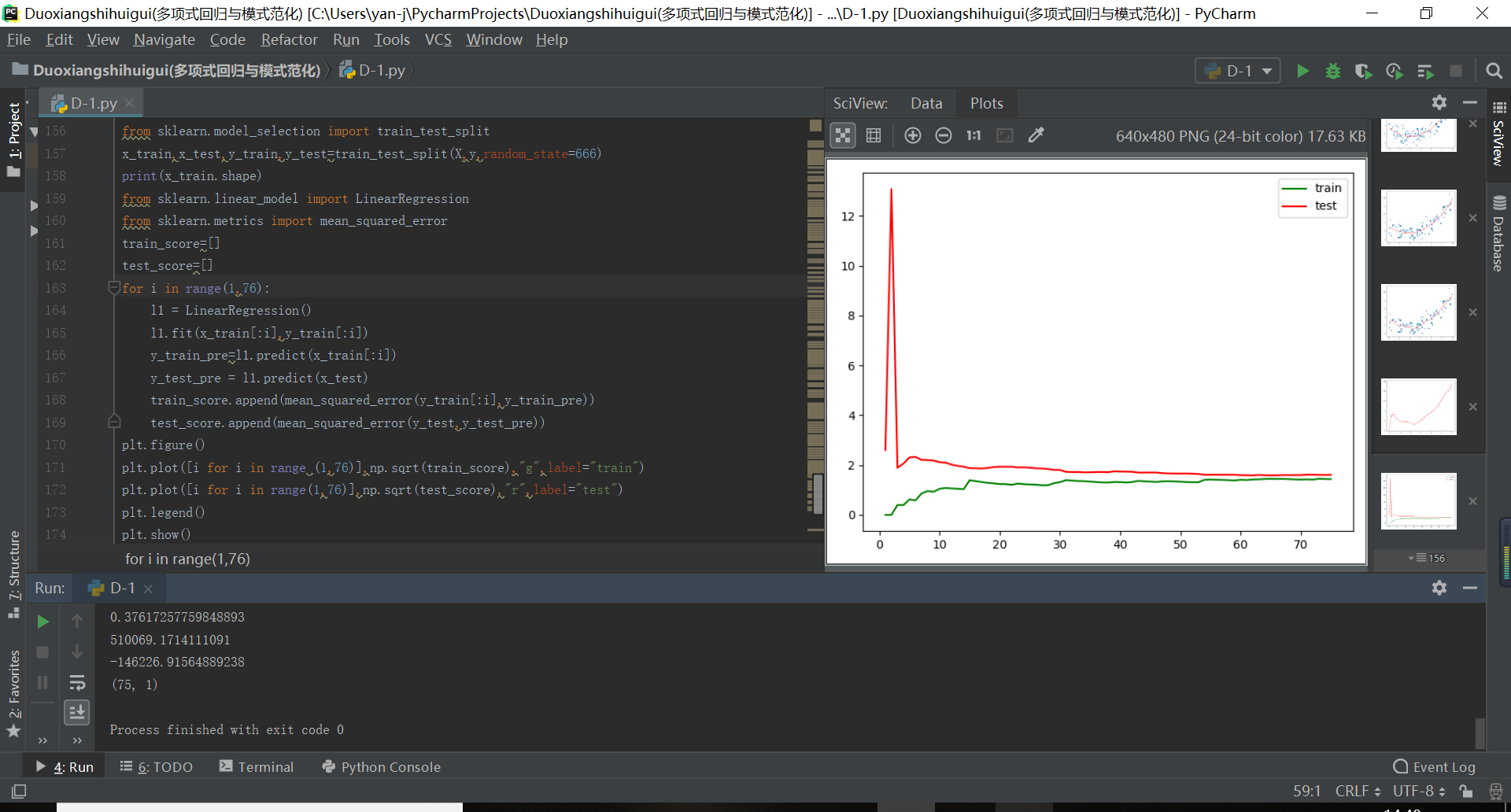
sklearn中的多项式回归算法的更多相关文章
- 【笔记】多项式回归的思想以及在sklearn中使用多项式回归和pipeline
多项式回归以及在sklearn中使用多项式回归和pipeline 多项式回归 线性回归法有一个很大的局限性,就是假设数据背后是存在线性关系的,但是实际上,具有线性关系的数据集是相对来说比较少的,更多时 ...
- sklearn中调用PCA算法
sklearn中调用PCA算法 PCA算法是一种数据降维的方法,它可以对于数据进行维度降低,实现提高数据计算和训练的效率,而不丢失数据的重要信息,其sklearn中调用PCA算法的具体操作和代码如下所 ...
- 机器学习实战基础(二十):sklearn中的降维算法PCA和SVD(一) 之 概述
概述 1 从什么叫“维度”说开来 我们不断提到一些语言,比如说:随机森林是通过随机抽取特征来建树,以避免高维计算:再比如说,sklearn中导入特征矩阵,必须是至少二维:上周我们讲解特征工程,还特地提 ...
- sklearn中的KMeans算法
1.聚类算法又叫做“无监督分类”,其目的是将数据划分成有意义或有用的组(或簇).这种划分可以基于我们的业务需求或建模需求来完成,也可以单纯地帮助我们探索数据的自然结构和分布. 2.KMeans算法将一 ...
- 机器学习实战基础(二十三):sklearn中的降维算法PCA和SVD(四) PCA与SVD 之 PCA中的SVD
PCA中的SVD 1 PCA中的SVD哪里来? 细心的小伙伴可能注意到了,svd_solver是奇异值分解器的意思,为什么PCA算法下面会有有关奇异值分解的参数?不是两种算法么?我们之前曾经提到过,P ...
- 机器学习实战基础(二十四):sklearn中的降维算法PCA和SVD(五) PCA与SVD 之 重要接口inverse_transform
重要接口inverse_transform 在上周的特征工程课中,我们学到了神奇的接口inverse_transform,可以将我们归一化,标准化,甚至做过哑变量的特征矩阵还原回原始数据中的特征矩阵 ...
- 机器学习实战基础(二十一):sklearn中的降维算法PCA和SVD(二) PCA与SVD 之 降维究竟是怎样实现
简述 在降维过程中,我们会减少特征的数量,这意味着删除数据,数据量变少则表示模型可以获取的信息会变少,模型的表现可能会因此受影响.同时,在高维数据中,必然有一些特征是不带有有效的信息的(比如噪音),或 ...
- 机器学习实战基础(二十七):sklearn中的降维算法PCA和SVD(八)PCA对手写数字数据集的降维
PCA对手写数字数据集的降维 1. 导入需要的模块和库 from sklearn.decomposition import PCA from sklearn.ensemble import Rando ...
- 机器学习实战基础(二十二):sklearn中的降维算法PCA和SVD(三) PCA与SVD 之 重要参数n_components
重要参数n_components n_components是我们降维后需要的维度,即降维后需要保留的特征数量,降维流程中第二步里需要确认的k值,一般输入[0, min(X.shape)]范围中的整数. ...
随机推荐
- vue cavnas绘制矩形,并解决由clearRec带来的闪屏问题
起因:在cavnas绘制矩形时 鼠标移动一直在监测中,所以鼠标移动的轨迹会留下一个个的矩形框, 要想清除矩形框官方给出了ctx.clearRect() 但是这样是把整个画布给清空了,因此需要不断 向画 ...
- vue中加载three.js的gltf模型
vue中加载three.js的gltf模型 一.开始引入three.js相关插件.首先利用淘宝镜像,操作命令为: cnpm install three //npm install three也行 二. ...
- Redis 简易消息队列
为了保持程序的高效,建议使用ProtoBuf. Google Protocol Buffer( 简称 Protobuf) 是 Google 公司内部的混合语言数据标准,目前已经正在使用的有超过 48, ...
- 「AHOI2014/JSOI2014」宅男计划
「AHOI2014/JSOI2014」宅男计划 传送门 我们首先要发现一个性质:存货天数随买食物的次数的变化类似于单峰函数. 具体证明不会啊,好像是二分加三分来证明?但是没有找到明确的严格证明. 感性 ...
- Linux下给mysql创建用户并分配权限
// fe_group 用户名// fe 数据库名// 123456 密码 1.新建用户 //登录MYSQL @>mysql -u root -p @>密码 //创建用户 mysql> ...
- scrapy中使用 IP 代理
在 scrapy 中使用 ip 代理需要借助中间件的功能 首先在settings 中设置好中间件,中间件优先级数字越小越先被执行 , } 然后编写中间件,拦截请求设置代理 class ProxyMid ...
- Java基础知识笔记第四章:类和对象
编程语言的几个发展阶段 面向机器语言 面向过程语言 面向对象语言:封装.继承.多态 类 类声明 class Person{ ....... } class 植物{ ....... } 类体 类使用 ...
- lua叠代器
注意:叠待值遇到nil就退出 叠代器,是符合for遍历框架,需要满足条件 1-叠代函数,常量,控制变量 2-叠代函数可以接受二个参数,当然也可以忽略处理(利用闭包封装参数作为控制变量和状态变量) 无状 ...
- ORACLE CPU过高的sql查询
1. 根据占用CPU高的进程号来查询这个进程执行的SQL语句: CPU过高的进程号: #首先找到CPU过高的进程号 # top -bn1 是静态找到占用最高的进程 [root@localhost ...
- SRS源码——调用FFmpeg参数问题
在SRS的Ingest功能中,会调用本地FFmpeg进行拉流转码, 调用的核心代码在srs_app_ffmpeg.cpp 的 SrsFFMPEG::start() 中: // memory leak ...
