ACM-Antiprime数
问题描述: swust打不开,随便找了个博客。。。。
对于任何正整数x,起约数的个数记做g(x).例如g(1)=1,g(6)=4.
定义:如果某个正整数x满足:对于任意i(0<i<x),都有g(i)<g(x),则称x为反素数.
现在给一个N,求出不超过N的最大的反素数.
比如:输入1000 输出 840
思维过程:
求[1..N]中最大的反素数-->求约数最多的数(约数同样多取数值小的)
简单证明:
如果X是答案,但X不是约数最多的数,假设约数最多的数是Y,那么Y>X,否则不符合反质数的定义。
那么很明显Y也是一个反质数,且Y比X大,那么答案应该是Y而不是X。
如果求约数的个数 756=2^2*3^3*7^1
(2+1)*(3+1)*(1+1)=24
基于上述结论,给出算法:按照质因数大小递增顺序搜索每一个质因子,枚举每一个质因子
为了剪枝:
性质一:一个反素数的质因子必然是从2开始连续的质数.
因为最多只需要10个素数构造:2,3,5,7,11,13,17,19,23,29
性质二:p=2^t1*3^t2*5^t3*7^t4.....必然t1>=t2>=t3>=....
//// Antiprime数.cpp : 定义控制台应用程序的入口点。
////
//
#include "stdafx.h" #include<cstdio>
#include<iostream>
using namespace std;
typedef long long ll;
int prime[] = { , , , , , , , , , , };
//相应的限制次数{ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11};
//2*3*5*7*11*13*17*19*21*23>n,所以只需考虑到23即可
ll n, BestSum, BestNum; //num表示当前数字大小、sum表示当前数字的约数个数、limit表示第k个素数的上限,k表示第k个素数
void solve(ll num, ll sum, ll limit, ll k)
{
//cout << "=======================: pos:" << k << "\tdiv:" << sum << "\tnum:" << num << "\tlimit:" << limit << endl;
if (sum>BestSum){
BestSum = sum;
BestNum = num;
}
else if (sum == BestSum&&num<BestNum){//约数个数一样时,取小数
BestNum = num;
}
for (int i = ; i <= limit; i++){//素数k取i个
cout << "=====================================================================" << endl;
cout << "now num:" << num << "\tk:" << k << "\ti:" << i << "\tlimit:" << limit << endl;
cout << num << "*prime[" << k << "]=" << "="<<num <<"*"<<prime[k]<< "=" << num * prime[k] << endl;
cout << "sum:" << sum << "\ti:" << i << "\tsum*(1+" << i << ")=" << sum*( + i) << endl;
cout << "=====================================================================" << endl<<endl;
num *= prime[k];
if (num>n) return;
solve(num, sum*( + i), i, k + );
}
}
int main(){
cin >> n;
solve(, , , );//每个数最多被分解成10质数的乘积
cout << BestNum;
return ;
}
下面是当n=20时,问题解的遍历图形。
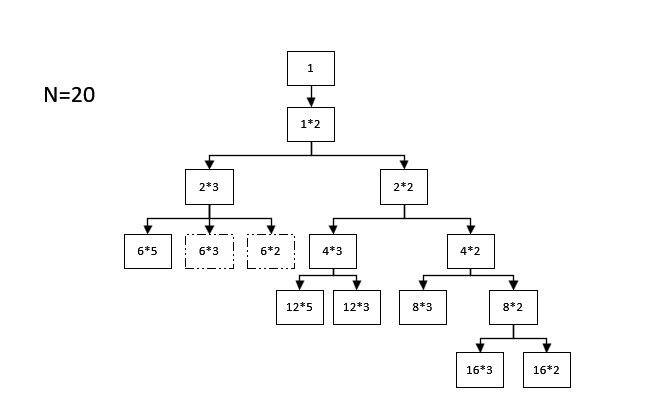
ACM-Antiprime数的更多相关文章
- [swustoj 373] Antiprime数
Antiprime数(0373) 问题描述 如果一个自然数n(n>=1),满足所有小于n的自然数(>=1)的约数个数都小于n的约数个数,则n是一个Antiprime数.譬如:1, 2, 4 ...
- COGS 693. [SDOI2005]Antiprime数 唯一分解定理逆用
693. Antiprime数 ★★ 输入文件:antip.in 输出文件:antip.out 简单对比 时间限制:1 s 内存限制:128 MB 如果一个自然数n(n>=1), ...
- Antiprime数-数论
题目描述 Description 如果一个自然数n满足:所有小于它的自然数的约数个数都小于n的约数个数,则称n是一个Antiprime数.譬如:1.2.4.5.12.24都是Antiprime数. ...
- 巴蜀1088 Antiprime数
Description 如果一个自然数n(n>=1),满足所有小于n的自然数(>=1)的约数个数都小于n的约数个数,则n是一个Antiprime数.譬如:1, 2, 4, 6, 12, 2 ...
- ACM 删数问题 SDUT 2072
http://acm.sdut.edu.cn/onlinejudge2/index.php/Home/Index/problemdetail/pid/2072.html 删数问题 Time Limit ...
- ACM——完数
完数 时间限制(普通/Java):1000MS/3000MS 运行内存限制:65536KByte 总提交:1930 测试通过:413 描述 自然数中,完数寥若晨 ...
- 南阳acm奇偶数分离
这道题的特殊要求是要先先限定了测试数据的组数,所以多加一条循环语句.下面是已通过的代码: #include<stdio.h> main() { int n,m,i,j; ...
- ACM 阶乘数位数
描述 N!阶乘是一个非常大的数,大家都知道计算公式是N!=N*(N-1)······*2*1.现在你的任务是计算出N!的位数有多少(十进制)? 输入 首行输入n,表示有多少组测试数据(n<1 ...
- ACM Fibonacci数 计算
Fibonacci数 时间限制:3000 ms | 内存限制:65535 KB 难度:1 描述 无穷数列1,1,2,3,5,8,13,21,34,55...称为Fibonacci数列,它可以递 ...
- ACM题目————数素数
令Pi表示第i个素数.现任给两个正整数M <= N <= 104,请输出PM到PN的所有素数. 输入格式: 输入在一行中给出M和N,其间以空格分隔. 输出格式: 输出从PM到PN的所有素数 ...
随机推荐
- Python实现简单中文词频统计示例
简单统计一个小说中哪些个汉字出现的频率最高: import codecs import matplotlib.pyplot as plt from pylab import mpl mpl.rcPar ...
- EC20的低功耗模式
EC20的支持以下几种工作模式,睡眠模式包括MCU主机睡眠和EC20睡眠. 当MCU主机不睡眠时,通过AT+QICSK =1(发送完之后串口被禁用不再响应AT指令),DTR=1(投票EC20可以进入睡 ...
- springmvc常用注解详解
1.@Controller 在SpringMVC 中,控制器Controller 负责处理由DispatcherServlet 分发的请求,它把用户请求的数据经过业务处理层处理之后封装成一个Model ...
- [aac @ ...] more samples than frame size (avcodec_encode_audio2)
在用FFmpeg对音频进行编码的时候报如下错误: [aac @ 000001cfc2717200] more samples than frame size (avcodec_encode_audio ...
- leetcode295 Find Median from Data Stream
""" Median is the middle value in an ordered integer list. If the size of the list is ...
- Lesson 13 The search for oil
What do oilmen want to achieve as soon as they strike oil? The deepest holes of all are made for oil ...
- 吴裕雄 Bootstrap 前端框架开发——Bootstrap 按钮:表示成功的动作
<!DOCTYPE html> <html> <head> <meta charset="utf-8"> <title> ...
- request-html
目录 基本使用 获取链接( links 与 absolute_links ) CSS 选择器与 XPATH 支持 JavaScript 自定义 User-Agent 模拟表单提交(POST) asyn ...
- Python 类型转换指南
一.int型 支持转换为 int 类型的,仅有 float.str.bytes,其他类型均不支持. 1.float -> int会去掉小数点及后面的数值,仅保留整数部分. 2.str -> ...
- Linux设备树学习
1.概念 设备树用于实现驱动代码与设备信息相分离.驱动代码只负责处理驱动的逻辑而关于设备的具体信息存放到设备树文件中.(dts文件,编译后为dtb文件).一个dts文件对应一个ARM的machine, ...
