自制spring中bean加载机制,仅做笔记自用
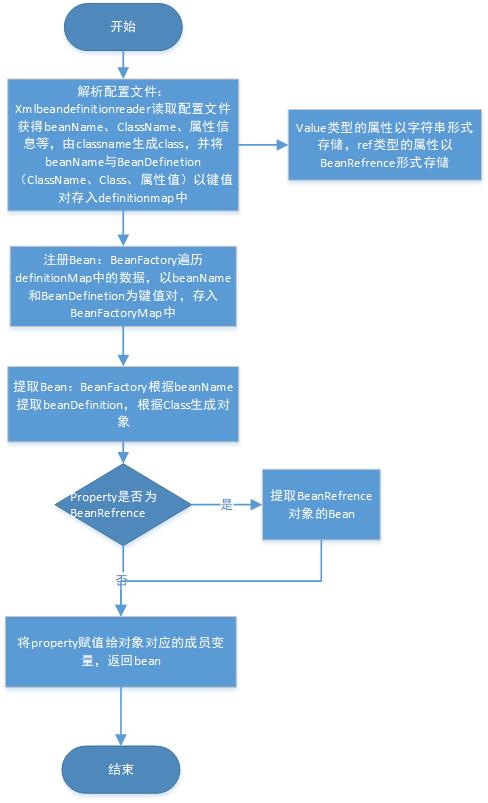
自制spring中bean加载机制,仅做笔记自用的更多相关文章
- Spring中ApplicationContext加载机制和配置初始化
Spring中ApplicationContext加载机制. 加载器目前有两种选择:ContextLoaderListener和ContextLoaderServlet. ...
- Spring中ApplicationContext加载机制
详见:http://blog.yemou.net/article/query/info/tytfjhfascvhzxcytp33 加载器目前有两种选择:ContextLoaderListener和Co ...
- 工厂模式模拟Spring的bean加载过程
一.前言 在日常的开发过程,经常使用或碰到的设计模式有代理.工厂.单例.反射模式等等.下面就对工厂模式模拟spring的bean加载过程进行解析,如果对工厂模式不熟悉的,具体可以先去学习一下工厂 ...
- 【spring】bean加载顺序
问题来源 有一个bean为A,一个bean为B.想要A在容器实例化的时候的一个属性name赋值为B的一个方法funB的返回值. 如果只是在A里单纯的写着: private B b; private S ...
- Spring IOC bean加载过程
首先我们不要在学习Spring的开始产生畏难情绪.Spring没有臆想的那么高深,相反,它帮我们再项目开发中制定项目框架,简化项目开发.它的主要功能是将项目开发中繁琐的过程流程化,模式化,使用户仅在固 ...
- ExtJs中动态加载机制研究(转)
觉得写的太好了,怕弄丢了,转一下:http://extjs.org.cn/node/659 昨天我们team对于extjs的动态加载机制做了些深入研究,这里先share下controller加载的结果 ...
- Spring中查看加载配置文件中 加载类的个数及详情
断点到: org.springframework.beans.factory.support.DefaultListableBeanFactory#getBeanDefinitionCount 显示该 ...
- tp中model加载机制
$user_model = D('User'); 如果当前模块下面有UserModel,就优先使用当前模块下的UserModel.如果当前模块下没有UserModel,就回去Common模块下找Use ...
- Node.js中模块加载机制
1.模块查找规则-当模块拥有路径但没有后缀时:(require(‘./find’)) require方法根据模块路径查找模块,如果是完整路径,直接引入模块: 如果模块后缀省略,先找同名JS文件,再找同 ...
随机推荐
- C++中的随机数
事情的开始是这样的,在大二的时候,写了几种排序算法,为了测试,就要为数组(或者容器)赋予一些随机初值,自然就用到了C/C++中的随机函数. 当时为了调用简单,将随机数赋值的过程写到了一个单独的函数里, ...
- winform跳转到bs
private void button7_Click(object sender, EventArgs e) { System.Diagnostics.Process.Start("http ...
- python的init函数里参数的作用
问题发现 一直有一个疑问,有时我们在继承时,在__init__函数会出现可变参数*arg或关键字参数**kw这样的参数,这些参数有什么用?如果有用,这些参数时如何传递?传递些什么? 注:如果你不知道什 ...
- Glove - sh demo.sh出错 Error: suffix or operands invalid for `vbroadcastss'
Glove+Python,使用预训练模型,执行sh demo.sh 报错:Error: suffix or operands invalid for `vbroadcastss' 解决:修改Makef ...
- 解题报告:luogu P1144 最短路计数
题目链接:P1144 最短路计数 很简单的一道\(dfs\),然而我又跑了一遍\(dij\)和排序,时间复杂度是\(O(nlog n)\) 注意:\(1\).搜索时向\(dis[j]=dis[cur] ...
- dstat 监控命令详解
一.工具介绍 dstat的man手册对于该工具的解释: dstat - versatile tool for generating system resource statistics 系统资源多用途 ...
- The Proof of Fibonacci GCD
\[\Large \text{The Proof of Fibonacci GCD}\] \[\text{By Sangber}\] \(\text{Fibonacci Sequence}\) \(\ ...
- C# 篇基础知识2——运算符、类型转换、流程控制、枚举、结构体和数组、函数
1.运算符.类型转换 计算某年y某月m某日d是周几的基姆拉尔森公式公式:int week = (d + 2*m + 3*(m + 1)/5 + y + y/4 - y/100 + y/400 + 1) ...
- ES6中 ,var,let和const的区别
var的特点 没有代码块的概念,全局范围内都有效 存在“变量提升”现象,即变量可以在声明之前使用,值为undefined let的特点 声明的变量仅在块级作用域内有效,存在了代码块的概念 不存在“变量 ...
- NO26 Linux的文件权限--chmod--Linux删除文件说明--suid--sgid
chmod命令改权限: suid: sgid:
