自动生成四则运算题目(C语言)

Github项目地址：https://github.com/huihuigo/expgenerator

合作者：马文辉（3118005015）、卢力衔（3118005013）

项目简介

1题目：实现一个自动生成小学四则运算题目的命令行程序（也可以用图像界面，具有相似功能）。

2说明：

自然数：0, 1, 2, …。

• 真分数：1/2, 1/3, 2/3, 1/4, 1’1/2, …。
• 运算符：+, −, ×, ÷。
• 括号：(, )。
• 等号：=。
• 分隔符：空格（用于四则运算符和等号前后）。
• 算术表达式：

e = n | e1 + e2 | e1 − e2 | e1 × e2 | e1 ÷ e2 | (e),

其中e, e1和e2为表达式，n为自然数或真分数。

• 四则运算题目：e = ，其中e为算术表达式。

3需求：

1. （完成）使用 -n 参数控制生成题目的个数，例如  Myapp.exe -n 10  将生成10个题目。

1. （完成）使用 -r 参数控制题目中数值（自然数、真分数和真分数分母）的范围，例如  Myapp.exe -r 10  将生成10以内（不包括10）的四则运算题目。
   该参数可以设置为1或其他自然数。该参数必须给定，否则程序报错并给出帮助信息。

1. （完成）生成的题目中计算过程不能产生负数，也就是说算术表达式中如果存在形如e1− e2的子表达式，那么e1≥ e2。
2. （完成）生成的题目中如果存在形如e1÷ e2的子表达式，那么其结果应是真分数。
3. （完成）每道题目中出现的运算符个数不超过3个。
4. （完成）程序一次运行生成的题目不能重复，即任何两道题目不能通过有限次交换+和×左右的算术表达式变换为同一道题目。
   例如，23 + 45 = 和45 + 23 = 是重复的题目，6 × 8 = 和8 × 6 = 也是重复的题目。3+(2+1)和1+2+3这两个题目是重复的，由于+是左结合的，1+2+3等价于(1+2)+3，也就是3+(1+2)，也就是3+(2+1)。但是1+2+3和3+2+1是不重复的两道题，因为1+2+3等价于(1+2)+3，而3+2+1等价于(3+2)+1，它们之间不能通过有限次交换变成同一个题目。

生成的题目存入执行程序的当前目录下的Exercises.txt文件，格式如下：

1. 四则运算题目1
2. 四则运算题目2

……

其中真分数在输入输出时采用如下格式，真分数五分之三表示为3/5，真分数二又八分之三表示为2’3/8。

1. （完成）在生成题目的同时，计算出所有题目的答案，并存入执行程序的当前目录下的Answers.txt文件，格式如下：

1. 答案1
2. 答案2

特别的，真分数的运算如下例所示：1/6 + 1/8 = 7/24。

1. （完成）程序应能支持一万道题目的生成。
2. （未完成）程序支持对给定的题目文件和答案文件，判定答案中的对错并进行数量统计，输入参数如下：

Myapp.exe -e <exercisefile>.txt -a <answerfile>.txt

统计结果输出到文件Grade.txt，格式如下：

Correct: 5 (1, 3, 5, 7, 9)

Wrong: 5 (2, 4, 6, 8, 10)

其中“:”后面的数字5表示对/错的题目的数量，括号内的是对/错题目的编号。为简单起见，假设输入的题目都是按照顺序编号的符合规范的题目。

PSP表格

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	30	40
· Estimate	· 估计这个任务需要多少时间	30	40
Development	开发	1080	1100
· Analysis	· 需求分析 (包括学习新技术)	120	120
· Design Spec	· 生成设计文档	60	70
· Design Review	· 设计复审 (和同事审核设计文档)	30	40
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	30	30
· Design	· 具体设计	120	120
· Coding	· 具体编码	480	480
· Code Review	· 代码复审	120	120
· Test	· 测试（自我测试，修改代码，提交修改）	120	120
Reporting	报告	90	80
· Test Report	· 测试报告	30	30
· Size Measurement	· 计算工作量	30	20
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	30	30
合计		1200	1220

需求分析及方案介绍

操作数相关的需求分析选取自1.5版本说明：

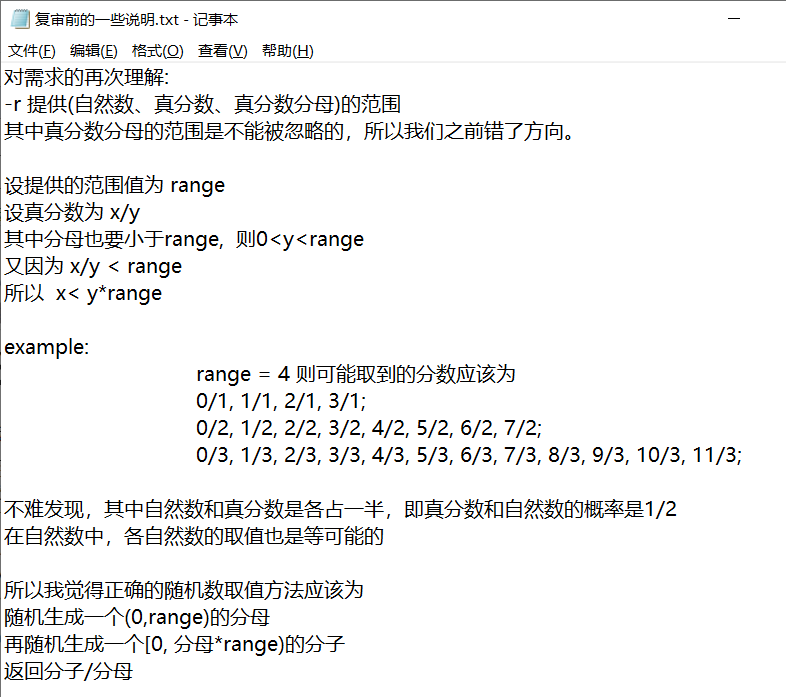
一些前言

　　采用的方案是将一条四则运算表达式转化为一棵相应的二叉树，表达式的运算顺序与二叉树的树形结构相对应，如果要求随机生成表达式，那么对应的表达式树的结构也是随机的。

所以，可以反向操作，随机生成表达式树的树形结构，也对应随机生成了一条表达式。

方案具体介绍（From 卢力衔，马文辉）：

方案总体是，先随机生成只有运算符的树形结构，在叶子结点加入操作数结点之后，就生成了一条表达式。

　　生成一条随机四则运算表达式的完整过程有 6 条步骤。

　　　　1.先生成当前表达式的运算符数量，再随机选择运算符；

　　　　2.将选择的运算符，组合成一个树形结构，也采用随机的方式；

　　　　3.在运算符树（只有运算符的树）的叶子结点上添加操作数（操作数也随机生成，思路就是上图的需求分析）；

　　　　　　4.判断生成的表达式合不合法（主要检测除数是否为0），如果合法则计算出表达式的结果；

　　　　　　5.检测是否与之前的表达式存在重复关系，即需求6的检测；

　　　　　　　　6.进行文件读写。

设计实现过程

整个程序分为4个cpp文件和1个头文件,分别为

Myapp.h　　　　　　　　　　　//结构体定义和函数声明

Myapp.cpp（main函数文件）　   //main函数中处理命令行参数和程序主逻辑

createExp.cpp　　　　　　　　  //有关创建一条表达式的函数实现，对应上述方案中的1、2、3点

judgeExp.cpp　　　　　　　　   //有关判断表达式的合法性和重复性的函数实现，对应上述方案中的4、5点

writeExpAndAnswer.cpp　　        //有关表达式写入文件的函数实现，对应上述方案中的6点

在一个功能模块编码之前，结对的两人先讨论好功能实现的方案，至少给出一个可行的方案，确定好方案之后，再实行编码。

由于这次的代码文件不大，所以就没用使用github进行版本的交接，而是通过微信相互发送文件，附上当前代码版本的改动说明，

同时一次交接后就更新版本号，便于区分不同阶段的代码。这次的结对项目经过了从1.0版本到最后的2.0版本。

下面是开发过程中的一些版本的说明：

       

具体设计过程：

第一阶段，不考虑重复性，合法性的检测和命令行参数的输入，先生成运算符的树形结构和添加操作数的操作，操作数考虑上减法和除法的要求；同时，完成在控制台中输出打印表达式的中缀表达式的函数实现。

第二阶段，考虑合法性的检测，显式上的除法已经不会出现1/0这样的表达式了，但是还是有可能生成6/(3 - 3)这样的表达式，因此需要加入合法性的检测。在合法性的检测，是通过计算该表达式的运算结果的方式来检测的。

第三阶段，考虑重复性的检测，例如题目中的(1 + 2) + 3与3 + (1 + 2)的重复情况，同时遇到了一种情况，一开始的输出结果都是在控制台中输出表达式，对于1 + （2 + 3）这种表达式，我们认为加法和乘法满足交换律，就省略了后面括号的输出，以至于出现了（1 * 1）/ 1和1 *（1 / 1）两种表达式都输出为1 * 1 / 1的形式，所以对表达式的中缀输出作了调整。

　　而且，我们的方案检测重复性是与前面生成的所有表达式进行比较，表达式树比较的函数是递归实现的，这样会出现一种循环+递归的代码结构，简单进行循环递归会导致程序运行速度变慢，这不是能接受的方案。因此，提出了先比较两条表达式的基本信息，先比较运算符数量，运算符是否相同，操作数是否相同，结果是否相同的基本信息，最大程度上减少递归比较的次数，只有在前面的基本信息都相同的情况下，才会触发最后的表达式树递归比较。

第四阶段，实现文件读写和命令行参数的输入，错误处理等，重新检查代码。

代码说明

文件中的代码，函数是有顺序的，在函数头的注释中可以找到当前函数的功能，参数和返回值。

//此处为Myapp.h头文件代码
#ifndef MYAPP_H_INCLUDED
#define MYAPP_H_INCLUDED

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <string.h>
#include <unistd.h>
#define TRUE 1
#define FALSE 0
typedef int Status;

//操作数结构体定义
typedef struct NumInfo{
    //denominator 分母, numerator 分子
    int numerator;
    int denominator;
} NumInfo;

//表达式树结点定义
typedef struct BiTNode{
    union {
        char opSym;         //运算符
        NumInfo numForm;    //操作数
    } value;

    int flag;   //0:value = opSym   1:value = num    -1:undefined
    struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;

//表达式基本信息结构体定义
typedef struct {
    BiTree ExpTree;     //表达式树
    int symCount;       //运算符个数
    char* symArr;       //运算符数组

    NumInfo* opNumArr;  //操作数数组
    NumInfo result;     //表达式结果
} ExpInfo, *ExpInfoPtr;

//生成运算符树部分的函数声明
char* chooseSym(int symNum);
BiTree createSymTree(int sym, char* symArr);
BiTNode* createSymNode(int& symArrIndex, char* symArr);

//插入操作数部分的函数声明
void addOpNumInSymTree(int numRange, BiTree symTree, int& flag);
void setNumForSubtraction(int &num1_numerator, int &num1_denominator, int &num2_numerator, int &num2_denominator, int numRange);
void setNumForDivision(int &num1_numerator, int &num1_denominator, int &num2_numerator, int &num2_denominator, int numRange);
void getRandomNum(int &numerator_, int &denominator_, int numRange);
BiTNode* createNumNode(int numerator, int denominator);

//检查表达式是否合法的函数声明，包含计算表达式的函数
Status isLegalExp(BiTree ExpTree, NumInfo& result);
NumInfo getValue(BiTree ExpTree, int&flag, int model);
int findGCD(int a, int b);
int findLCM(int a, int b);
NumInfo simplify(NumInfo numForm);

//检测是否为重复的表达式的函数声明
Status isRepetitive(ExpInfoPtr ExpArr, ExpInfo tempExpInfo, int ExpIndex);
Status ExpTreeCmp(BiTree T1, BiTree T2);
Status symArrCmp(char* arr1, char* arr2, int length);
Status opNumArrCmp(NumInfo* arr1, NumInfo* arr2, int length);
void addInExpArr(ExpInfoPtr ExpArr, ExpInfo tempExpInfo, int ExpIndex);
void getOpNumArr(BiTree ExpTree, NumInfo* OpNumArr, int& OpNumArrIndex);

//题目和答案文件读写函数的声明
Status Priority_com(char c1, char c2);
void writeExp(BiTree T, FILE* file);
void writeAnswer(NumInfo result, FILE* file);

#endif // MYAPP_H_INCLUDED

下面是Myapp.cpp代码，包含main函数：

 #include "Myapp.h"
 #include "createExp.cpp"
 #include "judgeExp.cpp"
 #include "writeExpAndAnswer.cpp"

 Status isNumString(char* str)
 {
     int i;
     for(i = ; i < strlen(str); i++)
         if(str[i] < '' || str[i] > '')
         return FALSE;
     return TRUE;
 }

 int main(int argc, char *argv[])
 {
     int questionCount = , numRange = ; 

     int opt;
     while((opt=getopt(argc,argv,"n:r:"))!=-)
     {
         switch(opt)
         {
             case 'n':   if(isNumString(optarg))   questionCount = atoi(optarg);
                         break;
             case 'r':   if(isNumString(optarg))   numRange = atoi(optarg);
                         break;
             default:    ;
         }
     }
     if( questionCount ==  || numRange ==  )
     {
         printf("命令行参数输入错误...\n");
         printf("输入格式为Myapp.exe -n 题目数(整数) -r 范围值(整数)\n");
         exit();
     }
     srand((int)time());

     FILE* questionFile,  *answerFile;
     questionFile = fopen("question.txt", "w");
     answerFile = fopen("answer.txt", "w");
     if(!questionFile || !answerFile)
     {
         printf("文件打开失败...按任意键退出\n");    getchar();
         exit();
     }

     ExpInfoPtr ExpArr = NULL;
     ExpArr = (ExpInfoPtr)malloc( (questionCount+) * sizeof(ExpInfo));
     if(!ExpArr)
     {
         printf("空间申请失败...按任意键退出\n");    getchar();
         exit();
     }

     int ExpIndex = ;
     int repetiveTime = ;
     int runtimeFlag = TRUE;

     while(ExpIndex <= questionCount)
     {
         //1、先生成运算符数量，再随机选择运算符
         int symCount = rand()% +;   //一条表达式最多选择3个运算符
         char* symArr = chooseSym(symCount);
         if(!symArr)
         {
             runtimeFlag = FALSE;
             break;
         }

         //2、运算符搭成树
         BiTree symTree = createSymTree(symCount, symArr);
         if(!symTree)
         {
             runtimeFlag = FALSE;
             break;
         }

         //3、在运算符树的叶子结点加操作数
         int addFlag = TRUE;
         addOpNumInSymTree(numRange, symTree, addFlag);
         if(addFlag == FALSE)
         {
             runtimeFlag = FALSE;
             break;
         }

         //4、判断生成的表达式是否合法，主要检测除数是否为0，并进行文件读写
         BiTree ExpTree = symTree;
         NumInfo result;

         if( isLegalExp(ExpTree, result) )
         {
             //5、表达式合法则检查重复性
             //5.1   先获取当前表达式的基本信息
             ExpInfo tempExpInfo;
             tempExpInfo.ExpTree = ExpTree;
             tempExpInfo.symCount = symCount;
             tempExpInfo.symArr = symArr;

             int opNumCount = symCount+;
             NumInfo* opNumArr = (NumInfo*)malloc( opNumCount*sizeof(NumInfo));
             if(!opNumArr)
             {
                 runtimeFlag = FALSE;
                 break;
             }

             int opNumArrIndex = ;
             getOpNumArr(ExpTree, opNumArr, opNumArrIndex);

             tempExpInfo.opNumArr = opNumArr;
             tempExpInfo.result = result;

             if(ExpIndex == )    //第二条题目开始需要检测重复性
                 addInExpArr(ExpArr, tempExpInfo, ExpIndex);
             else{

                 if( !isRepetitive(ExpArr, tempExpInfo, ExpIndex) )
                 {
                     //5.2.1 合法的话，则加入到表达式数组中
                     addInExpArr(ExpArr, tempExpInfo, ExpIndex);
                     repetiveTime = ;
                 }
                 else {
                         //5.2.2 不合法的话，生成重复次数更新，释放空间，防止范围为2，题目数为10000的恶意输入
                         repetiveTime++;
                         if(repetiveTime >= ExpIndex)
                             break;
                         free(opNumArr);
                         continue;
                 }
             }

             //6、在控制台、题目文件、答案文件打印题目序号
             printf("%d.\t", ExpIndex);
             fprintf(questionFile,"%d.\t", ExpIndex);
             fprintf(answerFile, "%d.\t", ExpIndex);

             //6.1 表达式写入题目文件
             writeExp(ExpTree, questionFile);
             printf("= ");
             fprintf(questionFile, "= \n");

             //6.2 写入答案文件
             writeAnswer(result, answerFile);

             //6.3 控制台展示运算过程
             //int flag = TRUE;
             //getValue(ExpTree, flag, 1);
             //printf("\n");

             //7、 更新题号
             ExpIndex++;
         }
     }

     //8、 生成完毕，关闭文件，释放表达式数组空间
     fclose(questionFile);
     fclose(answerFile);
     free(ExpArr);

     if(runtimeFlag == FALSE)
     {
         printf("空间申请失败...按任意键退出\n");    getchar();
         exit();
     }
     printf("\n当前已生成 %d 道，操作数范围为 %d 的四则运算题目.\n", ExpIndex-1, numRange);
     printf("题目保存在当前目录下的question.txt文件中\n答案保存在当前目录下的answer.txt文件中\n");
     return ;
 }

下面是createExp.cpp代码：

 #include "Myapp.h"
 /**
  * @function    选择当前生成的表达式中的运算符
  * @param       symNum:     运算符数量
  *
  * @return      symArr:     选择的运算符数组
  */
 char* chooseSym(int symNum)
 {
     char* symArr = NULL;
     char sym[] = {'+', '-', '*', '/'};
     symArr = (char*)malloc( symNum*sizeof(char));
     if(!symArr)
         return NULL;

     int i;
     for(i = ; i < symNum; i++)
         symArr[i] = sym[rand()%];

     return symArr;
 }

 /**
  * @function    根据传入的运算符数组索引创建运算符结点
  * @param       symArrIndex:    运算符数组索引;
                 symArr:         选择的运算符数组
  *
  * @return      nodePtr:        新创建运算符结点的指针
  */
 BiTNode* createSymNode(int& symArrIndex, char* symArr)
 {
     BiTNode* nodePtr = NULL;
     nodePtr = (BiTNode*) malloc(sizeof(BiTNode));

     if(!nodePtr)
         return NULL;

     nodePtr->flag = ;
     nodePtr->value.opSym = symArr[symArrIndex++];
     nodePtr->rchild = nodePtr->lchild = NULL;

     return nodePtr;
 }

 /**
  * @function    根据传入的运算符数组组成一棵树
  * @param       symCount:     运算符数量;
                 symArr:选择的运算符数组
  *
  * @return      T:只有运算符的树根结点指针
  */
 BiTree createSymTree(int symCount, char* symArr)
 {
     BiTree root = NULL;
     int symArrIndex = , i;
     root = createSymNode(symArrIndex, symArr);
     if(!root)
         return NULL;

     for(i = ; i < symCount-; i++)
     {
         BiTNode* newNodePtr = createSymNode(symArrIndex, symArr);
         BiTNode* temp = root;

         while()
         {
             //根据随机数，随机生成运算符的树形结构
             if(rand()%)
             {
                 if(!temp->lchild)
                 {
                     temp->lchild = newNodePtr;
                     break;
                 }
                 else temp = temp->lchild;
             }
             else {
                 if(!temp->rchild)
                 {
                     temp->rchild = newNodePtr;
                     break;
                 }
                 else temp = temp->rchild;
             }
         }
     }
     return root;
 }

 /**
  * @function    为传入的运算符树添加符合要求的操作数
  * @param       numRange:   操作数的范围
                 symTree:    运算符树
                 flag:       当前步骤是否成功的标记值，默认为TRUE
  *
  * @return      void
  */
 void addOpNumInSymTree(int numRange, BiTree symTree, int& flag)
 {
     //左孩子指针和右孩子指针都为空
     if(!symTree->lchild && !symTree->rchild)
     {
         //范围大于1，随机生成操作数
         if(numRange > )
         {
             int num1_numerator, num1_denominator;
             int num2_numerator, num2_denominator;

             //如果运算符是-和/，操作数有要求
             if( symTree->value.opSym == '-' )
                 setNumForSubtraction(num1_numerator, num1_denominator, num2_numerator, num2_denominator, numRange);

             else if( symTree->value.opSym == '/' )
                 setNumForDivision(num1_numerator, num1_denominator, num2_numerator, num2_denominator, numRange);

             else {
                 getRandomNum(num1_numerator, num1_denominator, numRange);
                 getRandomNum(num2_numerator, num2_denominator, numRange);
             }

             symTree->lchild = createNumNode(num1_numerator, num1_denominator);
             symTree->rchild = createNumNode(num2_numerator, num2_denominator);
         }
         else {
             //范围等于1，操作数只能为0
             symTree->lchild = createNumNode(, );
             symTree->rchild = createNumNode(, );
         }

         if(!symTree->lchild || !symTree->rchild)
             flag = FALSE;

         return;
     }

     //左孩子指针和右孩子指针都不为空
     else if( symTree->lchild && symTree->rchild)
     {
         addOpNumInSymTree(numRange, symTree->lchild, flag);
         addOpNumInSymTree(numRange, symTree->rchild, flag);
     }

     //左孩子指针和右孩子指针其中一个为空
     else
     {
         int _numerator, _denominator;
         getRandomNum(_numerator, _denominator, numRange);
         BiTNode* newNumNode = createNumNode(_numerator, _denominator);

         if(!newNumNode)
             flag = FALSE;

         //左孩子指针为空，则插入左孩子，否则插入右孩子
         if(!symTree->lchild){
             symTree->lchild = newNumNode;
             addOpNumInSymTree(numRange, symTree->rchild, flag);
         }
         else{
             symTree->rchild = newNumNode;
             addOpNumInSymTree(numRange, symTree->lchild, flag);
         }
     }
 }

 /**
  * @function     根据传入的数值创建运算数结点
  * @param        numerator:     操作数的分子
                  denominator:   操作数的分母
  *
  * @return       nodePtr:       操作数结点指针
 */
 BiTNode* createNumNode(int numerator, int denominator)
 {
     BiTNode* nodePtr = NULL;
     nodePtr = (BiTree)malloc(sizeof(BiTNode));
     if(!nodePtr)
         return NULL;

     nodePtr->flag = ;

     nodePtr->value.numForm.numerator = numerator;
     nodePtr->value.numForm.denominator = denominator;

     nodePtr->lchild = nodePtr->rchild = NULL;
     return nodePtr;
 }

 /**
  * @function    随机生成numRange范围内的操作数
  * @param       numRange:       操作数的范围
                 numerator:      操作数的分子部分
                 denominator:    操作数的分母部分
  *
  * @return      void
  */
 void getRandomNum(int &numerator_, int &denominator_, int numRange)
 {
     //denominator 分母, numerator 分子
     if(numRange != )
     {
         denominator_ = rand() % (numRange-) + ; // [1,numRange)
         numerator_ = rand() % (numRange*denominator_); //[0, numRange*denominator)
     }
     else {
         //范围numRange == 1， 操作数的分子只能为0， 分母设置为1
         denominator_ = ;
         numerator_ = ;
     }
 }

 /**
  * @function    为_减法_设置两个符合要求的操作数
  * @param       num1_numerator:     操作数1的分子
                 num1_denominator:   操作数1的分母
                 num2_numerator:     操作数2的分子
                 num2_denominator:   操作数2的分母
                 numRange:           操作数的范围
  *
  * @return      void
  */
 void setNumForSubtraction(int &num1_numerator, int &num1_denominator, int &num2_numerator, int &num2_denominator, int numRange)
 {
     double num1, num2;  //num1 - num2
     do{
         getRandomNum(num2_numerator, num2_denominator, numRange);
         num2 = (double)num2_numerator / (double)num2_denominator;

         getRandomNum(num1_numerator, num1_denominator, numRange);
         num1 = (double)num1_numerator / (double)num1_denominator;

     }while(num1 < num2);
 }

 /**
  * @function    为_除法_设置两个符合要求的操作数
  * @param       num1_numerator:     操作数1的分子
                 num1_denominator:   操作数1的分母
                 num2_numerator:     操作数2的分子
                 num2_denominator:   操作数2的分母
                 numRange:           操作数的范围
  *
  * @return      void
  */
 void setNumForDivision(int &num1_numerator, int &num1_denominator, int &num2_numerator, int &num2_denominator, int numRange)
 {
     double num1, num2;  //num1 / num2
     do{
         num2_denominator = rand() % (numRange-) + ;  // [1,numRange)
         num2_numerator = rand() % (numRange*num2_denominator - ) + ; // [1,numRange*num2_denominator) 除号情况除数不能为0这里需要处理
         num2 = (double)num2_numerator / (double)num2_denominator;

         getRandomNum(num1_numerator, num1_denominator, numRange);
         num1 = (double)num1_numerator / (double)num1_denominator;
     }while(num1 > num2);
 }

下面是judgeExp.cpp代码：

 #include "Myapp.h"
 /**
  * @function    表达式合法性检测，即能不能计算结果，能计算结果的返回计算结果
  * @param       ExpTree:    完整的表达式树
                 result:     存储合法表达式计算结果
  *
  * @return      flag:       当前表达式是否合法的标记
  */
 Status isLegalExp(BiTree ExpTree, NumInfo& result)
 {
     int flag = TRUE;
     result = getValue(ExpTree, flag, );
     return flag;
 }

 /**
  * @function    计算合法表达式的值，计算方式采用分数形式的计算
  * @param       ExpTree:    完整的表达式树
                 flag:       实时检测表达式是否合法的标记值
                 model:      控制台是否打印计算过程的标记值; 0:不打印计算过程， 1:打印
  *
  * @return      result:     当前表达式的计算结果
  */
 NumInfo getValue(BiTree ExpTree, int&flag, int model)
 {
     if(ExpTree->flag == )
         return ExpTree->value.numForm;
     else {
         NumInfo opNum1 = getValue(ExpTree->lchild, flag, model);
         NumInfo opNum2 = getValue(ExpTree->rchild, flag, model);
         NumInfo result;

         //通分，获得两个操作数分母的最小公倍数
         int LCM = findLCM(opNum1.denominator, opNum2.denominator);

         switch(ExpTree->value.opSym)
         {
             case '+' :  result.denominator = LCM;
                         result.numerator = opNum1.numerator*(LCM / opNum1.denominator) + opNum2.numerator*(LCM / opNum2.denominator);
                         break;

             case '-' :  result.denominator = LCM;
                         result.numerator = opNum1.numerator*(LCM / opNum1.denominator) - opNum2.numerator*(LCM / opNum2.denominator);
                         break;

             case '*' :
                         result.denominator = opNum1.denominator * opNum2.denominator;
                         result.numerator = opNum1.numerator * opNum2.numerator;
                         break;

             case '/' :
                         if(opNum2.numerator == )
                             flag = FALSE;
                         else {
                             result.denominator = opNum1.denominator * opNum2.numerator;
                             result.numerator = opNum1.numerator * opNum2.denominator;
                         }
                         break;
             default: ;
         }

         if(flag == TRUE)
         {
             result = simplify(result);
             if(model == )
                 printf("(%d/%d) %c (%d/%d) = %d/%d\n", opNum1.numerator, opNum1.denominator, ExpTree->value.opSym,
                                                     opNum2.numerator, opNum2.denominator, result.numerator, result.denominator);
         }
         else {
             result.numerator = ;
             result.denominator = ;
         }
         return result;
     }
 }

 /**
  * @function    寻找最大公约数，辗转相除法
  * @param       a:  参数1
                 b:  参数2
  *
  * @return      最大公约数
  */
 int findGCD(int a, int b)
 {
     if(a == )
         return b;
     return findGCD(b%a, a);
 }

 /**
  * @function    寻找最小公倍数，两数积除以最大公约数
  * @param       a:  参数1
                 b:  参数2
  *
  * @return      最小公倍数
  */
 int findLCM(int a, int b)
 {
     return (a*b)/findGCD(a, b);
 }

 /**
  * @function    化简分子和分母
  * @param       numForm:    一个用分子/分母表示的数
  *
  * @return      afterSim:   化简后的分子/分母表示的数
  */
 NumInfo simplify(NumInfo numForm)
 {
     NumInfo afterSim;
     if(numForm.numerator == )
     {
         afterSim.numerator = ;
         afterSim.denominator = ;
         return afterSim;
     }

     //寻找最大公因数
     int GCD = findGCD(numForm.denominator, abs(numForm.numerator));
     afterSim.numerator = numForm.numerator / GCD;
     afterSim.denominator = numForm.denominator / GCD;
     return afterSim;
 }

 /**
  * @function    检测当前生成的表达式是否与前面的题目重复
  * @param       ExpArr:         表达式数组
                 ExpTree:        当前表达式树
                 ExpIndex:       表达式数组的最后一个元素的索引
  *
  * @return      flag:   当前表达式是否与前面题目重复的标记值  FALSE:不重复,    TRUE:重复
  */
 Status isRepetitive(ExpInfoPtr ExpArr, ExpInfo tempExpInfo, int ExpIndex)
 {
     int flag = FALSE;
     int i;
     int tempExpInfoOpNumCount = tempExpInfo.symCount+;

     for(i = ; i < ExpIndex; i++)
     {
         ExpInfo temp = ExpArr[i];
         //1、比较表达式运算符数量
         if( tempExpInfo.symCount == temp.symCount )
             //2、比较表达式结果，分子分母对应相等
             if( tempExpInfo.result.denominator == temp.result.denominator && tempExpInfo.result.numerator == temp.result.numerator)
                     //3、比较表达式的运算符数组
                     if( symArrCmp(tempExpInfo.symArr, temp.symArr, tempExpInfo.symCount) )
                         //4、比较表达式的操作数数组
                         if( opNumArrCmp(tempExpInfo.opNumArr, temp.opNumArr, tempExpInfoOpNumCount) )
                             //5、比较表达式树的结构
                             if( ExpTreeCmp(tempExpInfo.ExpTree, temp.ExpTree) )
                             {
                                 flag = TRUE;
                                 break;
                             }
     }
     return flag;
 }

 /**
  * @function    检测表达式1的树结构和表达式2是否有重复关系
  * @param       T1:     表达式树1
                 T2:     表达式树2
  *
  * @return      flag:   表达式1和表达式2是否有重复关系的标记值, FLASE:不重复,    TRUE:重复
  */
 Status ExpTreeCmp(BiTree T1, BiTree T2)
 {
     if(T1->flag ==  T2->flag){ //结点类型相同
         if(T1->flag == ){ //都是操作数结点
             if(T1->value.numForm.numerator== && T2->value.numForm.numerator==)
                 return TRUE;
             else if(T1->value.numForm.numerator == T2->value.numForm.numerator
                && T1->value.numForm.denominator == T2->value.numForm.denominator)
                 return TRUE;
             else
                 return FALSE;
         }
         else if(T1->flag == ){ //都是操作符结点
             if(T1->value.opSym != T2->value.opSym)
                 return FALSE;
             // 操作符相同才递归比较
             else{
                 if(T1->value.opSym == '*' || T1->value.opSym == '+'){
                     int flag1, flag2;
                     flag1 = ExpTreeCmp(T1->lchild, T2->lchild) && ExpTreeCmp(T1->rchild, T2->rchild); //比较左左和右右的结果
                     flag2 = ExpTreeCmp(T1->lchild, T2->rchild) && ExpTreeCmp(T1->rchild, T2->lchild);  // 比较左右和右左的结果
                     return flag1 || flag2; //其中某一种相同则相同
                 }
                 else
                     return ExpTreeCmp(T1->lchild, T2->lchild) && ExpTreeCmp(T1->rchild, T2->rchild);
             }
         }
     }
     else
         return FALSE;

 }

 /**
  * @function    检测运算符数组1和数组2是否有重复关系
  * @param       arr1:     运算符数组1
                 arr2:     运算符数组2
                 length:   数组长度
  *
  * @return      flag:   运算符数组1和数组2是否有重复关系的标记值, FALSE:不重复,    TRUE:重复
  */
 Status symArrCmp(char* arr1, char* arr2, int length)
 {
     //由于是乱序的数组比较，采用辅助标记数组的方式
     int* flagArr = (int*) malloc(length * sizeof(int));
     if(!flagArr)
         return FALSE;

     int i, j;
     for(i = ; i < length; i++)
         flagArr[i] = ;

     for(i = ; i < length; i++)
     {
         for(j = ; j < length; j++)
             if(arr1[i] == arr2[j] && flagArr[j] ==  )
             {
                 flagArr[j] = ;
                 break;
             }
     }

     for(i = ; i < length; i++)
         if(flagArr[i] != )
             return FALSE;

     return TRUE;
 }

 /**
  * @function    检测操作数数组1和数组2是否有重复关系
  * @param       arr1:     操作数数组1
                 arr2:     操作数数组2
                 length:   数组长度
  *
  * @return      flag:     操作数数组1和数组2是否有重复关系的标记值, FALSE:不重复,    TRUE:重复
  */
 Status opNumArrCmp(NumInfo* arr1, NumInfo* arr2, int length)
 {
     //由于是乱序的数组比较，采用辅助标记数组的方式
     int* flagArr = (int*) malloc(length * sizeof(int));
     if(!flagArr)
         return FALSE;

     int i, j;
     for(i = ; i < length; i++)
         flagArr[i] = ;

     for(i = ; i < length; i++)
     {
         for(j = ; j < length; j++)
             if(arr1[i].numerator == arr2[j].numerator &&
                     arr1[i].denominator == arr2[j].denominator && flagArr[j] == )
             {
                 flagArr[j] = ;
                 break;
             }
     }

     for(i = ; i < length; i++)
         if(flagArr[i] != )
             return FALSE;

     return TRUE;
 }

 /**
  * @function    把当前表达式的基本信息存入表达式数组中
  * @param       ExpArr:         表达式数组
                 ExpInfo:        当前表达式的基本信息

  * @return      void
  */
 void addInExpArr(ExpInfoPtr ExpArr, ExpInfo tempExpInfo, int ExpIndex)
 {
     ExpArr[ExpIndex].ExpTree = tempExpInfo.ExpTree;
     ExpArr[ExpIndex].symCount = tempExpInfo.symCount;
     ExpArr[ExpIndex].symArr = tempExpInfo.symArr;
     ExpArr[ExpIndex].opNumArr = tempExpInfo.opNumArr;
     ExpArr[ExpIndex].result = tempExpInfo.result;
 }

 /**
  * @function    获取当前表达式的操作数，并记录在一个数组中
  * @param       ExpTree:        表达式树
                 opNumArr:       操作数数组指针
                 opNumArrIndex:  操作数数组索引
  *
  * @return      void
  */
 void getOpNumArr(BiTree ExpTree, NumInfo* opNumArr, int& opNumArrIndex)
 {
     if(ExpTree->flag == )
         opNumArr[opNumArrIndex++] = ExpTree->value.numForm;

     else{
         getOpNumArr(ExpTree->lchild, opNumArr, opNumArrIndex);
         getOpNumArr(ExpTree->rchild, opNumArr, opNumArrIndex);
     }
 }

下面是writeExpAndAnswer.cpp的代码：

 #include "Myapp.h"
 /**
  * @function    比较运算符优先级
  * @param       运算符c1, c2
  *
  * @return      Bool值
  */
 Status Priority_com(char c1,char c2){
     if((c1 == '+' || c1 == '-' || c1 == '*' || c1 == '/') && (c2 == '+' || c2 == '-' || c2 == '*' || c2 == '/'))
     {
         if(c1 == '*' || c1 == '/')
         {
             if(c2 == '+' || c2 == '-')
                 return TRUE;
             else
                 return FALSE;
         }
         else
             return FALSE;
     }
     else
         return FALSE;
 }

 /**
  * @function    将当前表达式写入题目文件
  * @param       T:      表达式树
                 file:   题目文件指针
  *
  * @return      void
  */
 void writeExp(BiTree T, FILE* file)
 {
     if(!T)
         return;

     if(T->lchild && T->lchild->flag == ){ //如果根节点与左子树的根节点是运算符
         if(Priority_com(T->value.opSym, T->lchild->value.opSym)){
             printf("( ");
             fprintf(file,"( ");
             writeExp(T->lchild, file);
             printf(") ");
             fprintf(file,") ");
         }
         else
             writeExp(T->lchild, file);
     }
     else
         writeExp(T->lchild, file);

     if(T->flag == ){
         printf("%c  ",T->value.opSym);
         fprintf(file,"%c  ",T->value.opSym);
     }
     else {
         int numerator = T->value.numForm.numerator;
         int denominator = T->value.numForm.denominator;

         if(numerator % denominator == ){ //自然数
             printf("%d  ",numerator/denominator);
             fprintf(file,"%d  ",numerator/denominator);
         }
         else{
             if(numerator < denominator){ //真分数
                 printf("%d/%d  ",numerator,denominator);
                 fprintf(file,"%d/%d  ",numerator,denominator);
             }
             else{ //带分数
                 printf("%d\'%d/%d  ",numerator/denominator,numerator%denominator,denominator);
                 fprintf(file,"%d\'%d/%d  ",numerator/denominator,numerator%denominator,denominator);
             }
         }
     }

     if(T->rchild && T->rchild->flag == ){ //如果根节点与右子树的根节点是运算符
             printf("( ");
             fprintf(file,"(  ");
             writeExp(T->rchild, file);
             printf(") ");
             fprintf(file,")  ");
     }
     else
         writeExp(T->rchild, file);
 }

 /**
  * @function    将当前表达式写入答案文件
  * @param       T:      表达式树
                 file:   答案文件指针
  *
  * @return      void
  */
 void writeAnswer(NumInfo result, FILE* answerFile)
 {
     int numerator = result.numerator;
     int denominator = result.denominator;
     if(numerator % denominator == ){ //自然数
         printf("%d\n",numerator/denominator);
         fprintf(answerFile,"%d\n",numerator/denominator);
     }
     else{
         if(abs(numerator) < abs(denominator)){ //真分数
             printf("%d/%d\n",numerator,denominator);
             fprintf(answerFile,"%d/%d\n",numerator,denominator);
         }
         else{ //带分数
             printf("%d\'%d/%d\n",numerator/denominator,abs(numerator)%denominator,denominator);
             fprintf(answerFile,"%d\'%d/%d\n",numerator/denominator,abs(numerator)%denominator,denominator);
         }
     }
 }

---

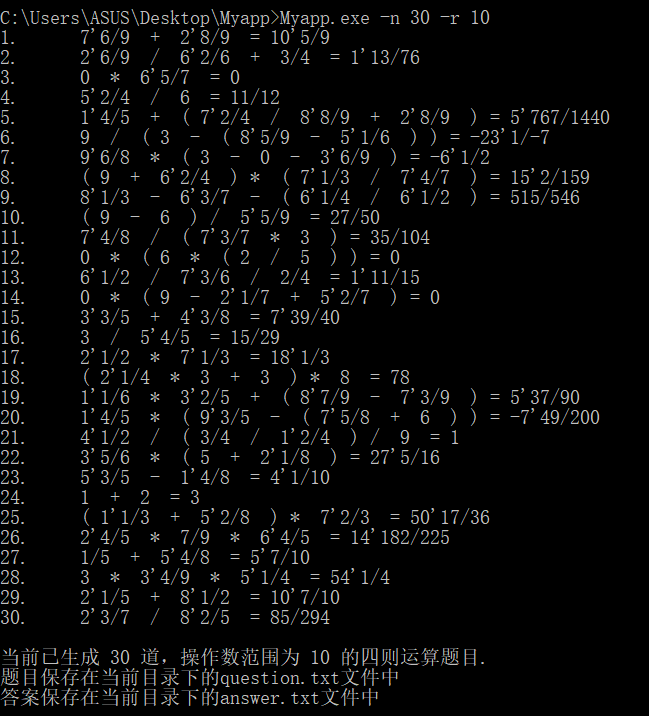
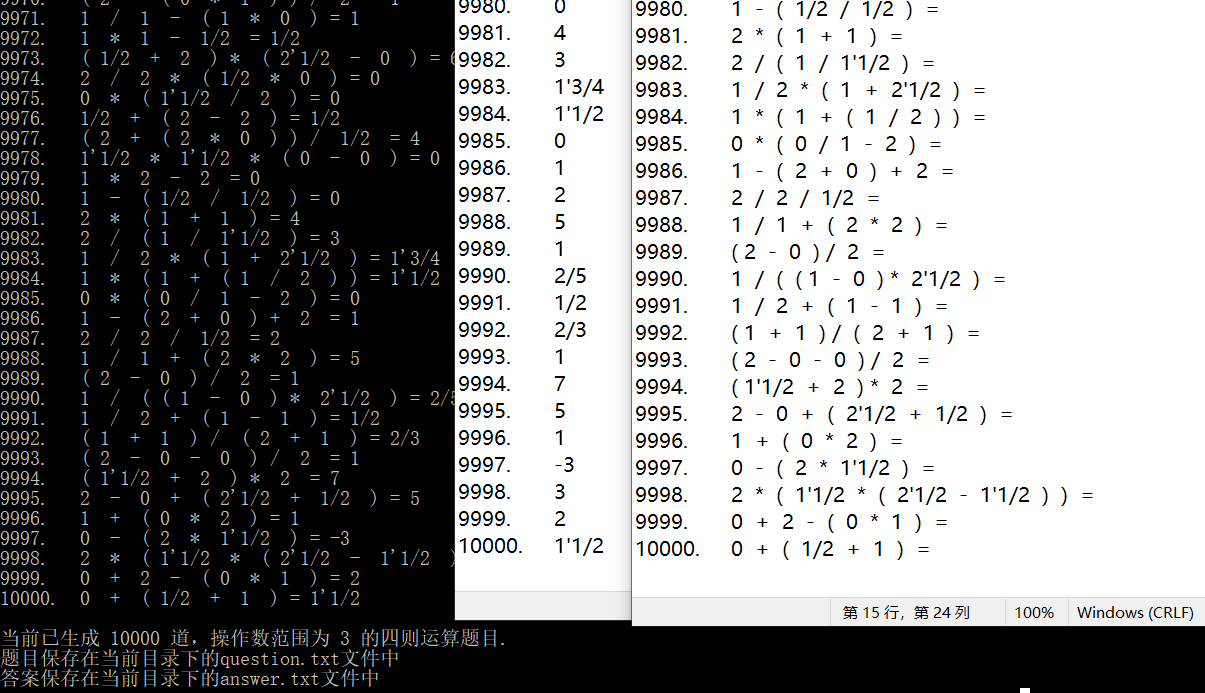
测试运行

 

    

项目小结

　　这次项目是结对项目，需要两个人的合作，一个人编码，一个人设计复审，角色轮流交换。每个阶段都有不同的责任，项目采用功能分块，由简入繁的过程开发，还记得最初的版本，只有一个main函数，两个调用的函数，没用命令行，参数固定，再到后面参数改变，不断测试，有时在测试中找到的是之前写的函数的bug，属实尴尬，不过通过不断的代码复审，代码阅读，时常灵光一闪，这段删掉，这段补上，if-else丢得只剩一个，逻辑简化，效果更佳。也有讨论到入夜已深，手机常亮，想法迸发，落魄发现，方案搞笑，打回重想。但是，个中滋味，回味如甘，编码乐趣，在于敲下。